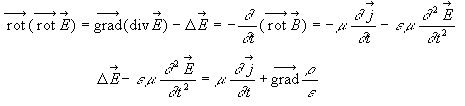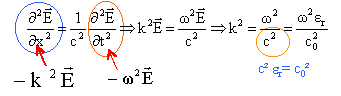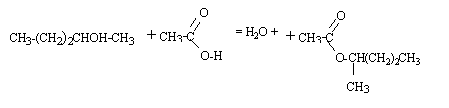|
chlorure d'argent ; oxydoréduction ; chimie organique : pent-2-ène d'après concours inspecteur de la concurrence, de la consommation et de la répression des fraudes En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||
| .
. |
|||
|
|||
|
Soit u= U 2½ cos (wt) la tension instantanée à la date t aux bornes d'un dipôle électrique ; U est la tension efficace, w est la pulsation de la tension. L'intensité du courant qui le traverse est i= I 2½ cos(wt+j) ; I est l'intensité efficace, j le déphasage.
corrigé puissance instantanée p consommée par le dipôle : p= u i = 2UI cos (wt)cos(wt+j) p = UI (cos ( 2wt+j) + cos j) puissance moyenne P : P= UI cos j soit I= P/(U cosj)= 104 / (220*0,7) =64,9 A. admittance = inverse d'une impédance ; | Y | = I/U = 64,9 / 220 = 0,295 S. condensateur et moteur sont montés en dérivation : les admittances du moteur et du condensateur ( jCw) s'ajoutent. Yt=Y + jCw= | Y | e-j j + jCw. l’association {condensateur+moteur} étant purement résistive, Yt= est un nombre réel ; sa partie imaginaire est donc nulle. Yt = | Y | cosj -j | Y |sinj +jCw ; -j ; -j|Y |sinj +jCw=0 ; C= |Y |sinj/ w. avec w = 2 pf = 2*3,14*50 = 314 rad/s ; sinj= 0,714 ; |Y | =0,295 S C= 0,295*0,714 / 314 = 6,7 10-4 F. la puissance moyenne consommée par le condensateur est nulle. P active totale = P active moteur = 10 kW Q réactive totale = Q réactive condensateur = -CwU² = -6,7 10-4*314*220²= -10,2 var S²= P²+Q² = 10²+10,2²= 204,1 ; S= 14,3 VA Or S=UI soit I= 14,3 103/ 220 = 65 A.
|
|||
|
On considère, un cylindre homogène en cuivre, de longueur b et de rayon a, parcouru par un courant électrique uniforme et constant d'intensité I. Caractéristiques du cylindre dans les conditions de l'étude : • résistivité électrique r=2,0.10-8 W m ; • conductibilité thermique : l = 400 W K-1m-1. • a=1,0 mm. On suppose que l'énergie thermique produite dans le conducteur est dissipée radialement par conduction et on néglige les effets de bord. On rappelle que la résistance R d’un conducteur cylindrique homogène résistivité électrique r, de longueur b et de section S, est donnée par la relation : R=rb/S
corrigé puissance P dissipée : P= RI² avec R=rb/S et S= pa² ; p= rbI²/(pa² ) volume du cylindre V= pa²b puissance p dissipée par unité de volume p= P/V = rI²/(pa² )2 en Wm-3. flux thermique de conduction qui entre par une surface cylindrique de longueur b et de rayon r : -l* surface latérale de rayon r * dT/dr = -l 2pr b(dT/dr )r. flux thermique de conduction qui sort par une surface cylindrique de longueur b et de rayon r+dr : -l* surface latérale de rayon r +dr * dT/dr = -l 2p(r+dr)b(dT/dr )r+dr. élément de volume compris entre les surfaces cylindriques de rayons r et r+dr : dv= 2prbdr puissance interne dans cet élément de volume : pdv = 2pbp rdr bilan énergétique en régime permanent : 2pbp rdr -l 2pr b(dT/dr )r. + l 2p(r+dr)b(dT/dr )r+dr=0 p rdr -l r [dT/dr ]r + l (r+dr)[dT/dr ]r+dr=0 p rdr +l d (r dT/dr )=0 ou -pr/ l= d(rdT/dr)/dr d(rdT/dr)/dr= -p/l r s'écrit : dT/dr+ r d²T/dr²+p/l r =0 solution du type T= ar²+br+c ; dT/dr= 2ar+b ; d²T/dr²= 2a. 2ar+b+ 2ar + p/l r =0 soit b = 0 et a = - p/(4l) ; T= - p/(4l)r² + c; si r =0, T=c=T0 ; si r = a, T= -p/(4l) a² +T0 ; DT= p/(4l) a². or p= rI²/(pa² )2 d'où DT= rI²/(p2a² 4l). application numérique : DT=2 10-8*400/(3,14²*10-6*4*400)=0,005 °C. la section du fil est proche de 3 mm², celui-ci est tout à fait capable de supporter sans dommage un courant d'intensité 20 A. |
|||
|
Dans cet exercice les grandeurs complexes sont soulignées et on utilise le nombre complexe j telle que j2=-1. Soit un milieu diélectrique
caractérisé par sa permittivité
relative complexe : er
= e 1-je2.
Le champ magnétique B et le champ
électrique E à l’intérieur
du milieu sont liés par l’équation
différentielle de Maxwell Ampère :
relation de dispersion: k²= erw²/c² dériver deux fois E par rapport au temps et par rapport à x.
k=w/c( n1-jn2) ; k²= w²/c² (n1²-n2² - 2jn1n2) d'autre part k²= erw²/c² =( e 1-je2)w²/c² par identification des parties réelle et imaginaire, il vient : n1²-n2²= e 1 ; 2n1n2= e2. n1²-n2²= 4 ; n1n2= 2 soit n2= 2/n1 ; n1²-4/ n1²= 4 n14- 4 n12- 4
= 0 ; on pose X= n1² ; X²-4X-4=0 ; X=
4,83 ; n1 = 2,2 et
n2=0,91.
j(wt-w/c( n1-jn2)z) = j(wt -n1z/c)-n2wz/c suivant l'axe des x : E= E0 exp[ j(wt -n1z/c)-n2wz/c] E= E0 exp[-c/(n2w z)] exp[ j(wt -n1z/c)]= E0 exp[ n2w z/c ] exp[ j(wt -n1z/c)] l’onde pénètre dans le milieu sur une profondeur caractéristique d = c/(n2w ) c=3 108 m/s ; f =2,45 GHz =2,45 109 Hz ; w = 2pf = 1,54 1010 rad/s. d = 3 108 / (0,91*1,54 1010 ) = 2,1 10-2 m = 2,1 cm.
|
|||
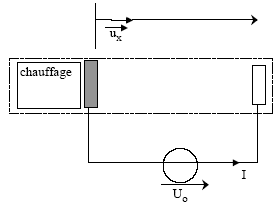
Données : e= 1,6 10-19 C ; m=0,91 10-30 kg ; 36pe0=10-9 SI ; h= 2,0 cm ; S= 1,0 cm2.
énergie totale W(0) d’un électron
à l’abscisse x=0 : W(0) = 0 densité de courant j ( vecteur) en fonction de I, S et du vecteur unitaire ux : j = I / S ux relation entre la densité de courant j , la charge volumique d’espace r et la vitesse vx : Quantité d'électricité traversant la section S en dt seconde : Idt ; ces charges se trouvait dans le volume Sdx = Svdt d'où Idt = r S v dt ; I = r S v ; j = r v ux Expression de la charge volumique d’espace r en fonction de I, de Ux et des paramètres du système : j = r v ux = I / S ux ; v²= 2e/m U(x). r
[2e/m
U(x)]½=I/S ; r=
I/S [2e/m
U(x)]-½.
repport dans l'équation différentielle : Cn(n-1) xn-2 +r/e0=0 donne n=2 et C= -r/(2e0). Ux = -r/(2e0) x2 caractéristique courant-tension donnant l’intensité I en fonction de la tension Uh. Ux = -r/(2e0) x2 ; r= I/S [2e/m U(x)]-½ ; I = rS[2e/m U(x)]½ avec r = - Ux2e0 x-2 ; I = - 2e0 x-2 S[2e/m ]½Ux1,5. le signe négatif traduit le fait que le courant I va en sens contraire de l'axe des x. Calculer l’intensité I pour Uh = 500 V. [2e/m ]½ = [3,2 10-19/ 0,91 10-30]½ =5,9 105 ; e0=10-9 /(36p)= 8,84 10-12 ; 5001.5=1,12 104 I =2*8,84 10-12 *10-4* 5,9 105 *1,12 104 /(4 10-4)= 2,9 10-2 A = 29 mA.
|
|||
|
Données : produit de solubilité à 25°C: Ks[AgCl(s)] = 10-10. Ks[Ag2CrO4(s)] = 10-12. Le nitrate d’argent AgNO3(s) se dissocie totalement dans l’eau.
corrigé AgCl(s) =Ag++ Cl- . potentiel chimique de l'ion argent : mAg = m°Ag + RT ln [Ag+] potentiel chimique de l'ion chlorure : mCl = m°Cl + RT ln [Cl-] enthalpie G = mAg +mCl = m°Ag + m°Cl + RT ln ([Ag+] [Cl-]) avec m°Ag + m°Cl = -RT ln Ks ; G = -RT ln Ks + RT ln ([Ag+] [Cl-]) G est négative( évolution de la réaction dans le sens direct) si [Ag+] [Cl-] <Ks. G est positive ( évolution
de la réaction dans le sens inverse,
précipitation de AgCl ) si [Ag+]
[Cl-] >Ks.
n0 = 10-6 mol dans 1 L; n0 est inférieur à s, dissolution du solide AgCl. n0 = 10-3 mol dans 1 L ; n0 est supérieur à s, dissolution partielle du solide AgCl ; [Ag+]= [Cl-] = 10-5 mol/L si on ajoute 10-3 mol de AgCl(s) : [Ag+]= [Cl-] = 10-5 mol/L, pas de changement. si on ajoute 10-3 mol de NaCl(s), la concentration en ion chlorure est voisine de [Cl-]= 10-3 mol/L la concentration de l'ion argent devient : Ks/
[Cl-] = 10-10 /
10-3 = 10-7 mol/L ; on observe la
précipitation de AgCl par effet d'ion commun
ajouté.
Pile à construire pour mesurer [Ag+] : une demi-pile de référence ; l'autre demi-pile contient une électrode d'argent plongeant dans une solution satutée de chlorure d'argent. E= E°( Ag+/Ag) + RT/F log
[Ag+]
v0 (mL) : volume nitrate d'argent ajouté avant précipitation AgCl, très faible devant 55 mL, on néglige la dilution. [Ag+]= 10-10/9 10-3 = 1,1 10-8 mol/L : v0 = 1,1 10-8 /0,05= 2,2 10-7 L = 2,2 10-4 mL. Ag2CrO4 précipite dès que : [Ag+]2 = 10-12 / [CrO42-]0 avec [CrO42-]0 = 2,5 10-4 /55 10-3 = 4,5 10-3 mol/L [Ag+]2 = 10-12 /4,5 10-3 = 2,2 10-10 ; [Ag+] = 1,5 10-5 mol/L. Donc AgCl(s) précipite le premier, puis Ag2CrO4 (s) précipite dès que [Ag+] = 1,5 10-5 mol/L. concentration Ag+ avant l'équivalence : v (L) AgNO3 ajouté [Cl-]=(5 10-4 - 0,05 v)/ (0,055+v) ; [Ag+]= 10-10*(0,055+v)/ (5 10-4 - 0,05 v) à l'équivalence : c0VE= 0,05 VE= 5 10-4 soit VE= 0,01 L = 10 mL. un peu avant l'équivalence [CrO42-] = 2,5 10-4 /65 10-3 = 3,8 10-3 mol/L Or Ag2CrO4 (s) précipite dès que [Ag+]² = 10-12 /3,8 10-3 = 2,63 10-10 ; [Ag+] = 1,6 10-5 mol/L 10-10*(0,055+v)/ (5 10-4 - 0,05 v) = 1,6 10-5 0,055+v=1,6 105*(5 10-4 - 0,05 v) 0,055+ v = 80 - 8 103 v ; 80 -0,055 = (8 103 +1) v ; v= 9,99 10-3 L en conséquence les ions chlorure précipitent pratiquement tous avant que les ions chromate ne précipitent.
|
|||
|
Soit les deux couples rédox suivants dont on indique les potentiels redox standards E°. E°1(NO3-/NO(g)) = 0.96 V et E°2(Pt2+/Pt(s)) = 1.2 V. Le complexe Pt(Cl)42- se dissocie pour donner l’ion Pt2+ et les ions chlorure Cl- selon l’équilibre chimique suivant de constante d’équilibre thermodynamique Kd = 10-16: Pt(Cl)42- = Pt2++ 4Cl-
corrigé Pt = Pt2+ + 2e- ; E2= 1,2 + 0,03 ln [Pt2+] Pt(Cl)42- = Pt2++ 4Cl- avec 10-16 = [Pt2+][Cl-]4 / [Pt(Cl)42-] E2= 1,2 + 0,03 ln (10-16[Pt(Cl)42-] /[Cl-]4 ) E2= 1,2 -16*0,03+ 0,03 ln ([Pt(Cl)42-] /[Cl-]4 ) E2=0,72 +0,03 ln ([Pt(Cl)42-] /[Cl-]4 ) cete valeur peut être inférieure à 0,96 V, potentiel redox du couple (NO3-/NO(g)) : le platine peut donc être oxydé en présence d'acide nitrique et d'acide chlorhydrique. 3 fois {Pt + 4Cl- = Pt(Cl)42- + 2e- }oxydation 2 fois { NO3- + 3 e- + 4H+ = NO + 2H2O } réduction faire la somme : 3 Pt + 12Cl- + 2 NO3- + 8H+ = 3 Pt(Cl)42- +2NO + 4H2O oxydo-réduction |
|||
|
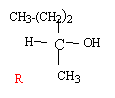
Dans ce problème, le pent-2-ène subit une série de réactions chimiques successives. On vous demande d’identifier les divers produits de réaction.
corrigé 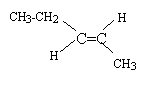
C5H10 + H2O --> C5H12 O l'acide ( ion H+) est un catalyseur; l'acide sulfurique est utilisé ; l'acide chlorhydrique ( présence d'ion chlorure ) peut conduire à un chloroalcane. réaction d'addition électrophile sur une double liaison carbone carbone ; le premier stade lent conduit à un carbocation; le second stade rapide est une attaque nucléophile sur le carbocation. L'addition d'un réactif dissymétrique H-OH noté H-X sur un alcène dyssimétrique peut conduire à deux produits : d'après la règle de Markownikoff l'hydrogène se fixe sur le carbone de la double liaison qui possède le plus grand nombre d'hydrogène. Ici, chaque atome de carbone de la double liaison portant un atome d'hydrogène, on ne peut pas prévoir le produit majoritaire. Le pentan-2-ol possédant un carbone asymétrique est chiral. On obtient un mélange racémique car le carbocation intermédiaire est plan et l'attaque nucléophile par HO- peut se faire d'un coté ou de l'autre du plan avec la même probabilité.
B est traité par l’hydrure de sodium (NaH) pour donner un intermédiaire réactionnel C : C5H11O- . C5H11OH + Na+ + H- --> C5H11O- + Na+ + H2 C opposé au bromure d’éthyle, à température ambiante, conduit au produit D : ( éther) : oxyde d'éthyle et de 1-méthylbutyle . C5H11O- +
C2H5Br -->
C5H11O -C2H5 +
Br-. substitution SN2. En présence d’acide acétique CH3CO2H et de proton H+ le dérivé B donne un dérivé F : éthanoate de 1-méthylbutyle
- addition de l'ion hydroxyde sur le groupe carboxyle de l'ester avec formation d'un intermédiaire tétraédrique. - fragmentation de l'intermédiaire tétraédrique avec élimination d'un ion alcoolate. -déprotonation de l'acide carboxylique par l'ion alcoolate avec formation d'un ion carboxylate.
alcool secondaire + dichromate de potassium K2Cr2O7 en milieu acide --> cétone. Cr2O72- + 14H+ + 6e- = 2Cr3+ +7H2O réduction 3 R-CHOH-R' =3 R-CO-R' + 6H+ + 6e- oxydation. faire la somme : Cr2O72- +3 R-CHOH-R' + 8H+ = 2Cr3+ +7H2O+3 R-CO-R' oxydoréduction 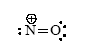
|
|||
|
|
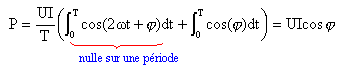
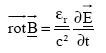 ;
c est la célérité des ondes
électromagnétiques dans le vide.
;
c est la célérité des ondes
électromagnétiques dans le vide.