A la surface d’un lac, on dépose deux bouchons A et B distants de 1 m. On lance une pierre qui tombe verticalement au voisinage de A ; des rides se propagent à la surface de l’eau. On déclenche le chronomètre quand la première ride atteint le bouchon A, puis on arrête le chronomètre quand cette ride arrive en B. Le chronomètre indique un temps de 2,0 s.

a) L’onde qui se propage à la surface de l’eau est une onde longitudinale.

b) La célérité de l’onde a pour valeur 2 m.s^-1.

c) L’onde transporte de l’énergie mécanique.

d) Le bouchon A se rapprochera du bouchon B.

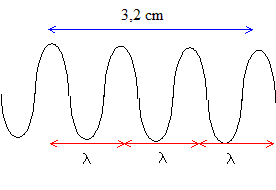
Dans une cuve à ondes, une pointe est animée, grâce à un vibreur, d’un mouvement rectiligne périodique de direction verticale, d’axe y’y orienté vers le bas, d’amplitude 5 mm, de fréquence 50 Hz. A t = 0, la pointe se situe en y = 0 et descend. On observe, dans la cuve à ondes, quatre crêtes successives d’ondes circulaires séparées de 3,2 cm.

a) La longueur d’onde a pour valeur 0,8 cm.

b) La célérité de l’onde a pour valeur 0,4 m.s^-1.

c) Deux points A et B à la surface de l’eau, séparés de 10 cm, vibrent en phase.

d) L’équation horaire de la pointe est y(t) = 5 × 10^-3 sin (100 p t), y étant exprimé en mètre, t en seconde.

Une radiation a, dans le vide, une longueur d’onde égale à 600 nm et, dans un milieu transparent, une longueur d’onde égale à 400 nm. La célérité de la lumière dans le vide est c = 3 × 10⁸ m.s^-1.

a) Dans le vide, la fréquence de cette radiation a pour valeur 5 × 10¹⁴Hz.

b) Dans le milieu transparent la fréquence de cette radiation est supérieure à 5 × 10¹⁴Hz.

c) L’indice du milieu est de 1,5.

d) Dans le milieu transparent la longueur d’onde est voisine de l’infrarouge.

Le brome 77 est un isotope radioactif, de demi-vie T égale à 57 heures, utilisé en imagerie médicale. Le noyau fils est le Sélénium 77. On considère un échantillon dont l’activité initiale est de 6,0 × 10¹⁵ Bq. Chaque particule émise à cet instant a une vitesse v d’éjection.

Données : numéro atomique de Br : Z = 35 ; numéro atomique du sélénium Se : Z = 34 ; ln2 voisin 0,7 ; 57 × 3600 voisin 0,21 × 10⁶,

m (positon) proche 10^-30 kg, vitesse d’éjection de la particule : v = 2 × 10⁸ m.s^-1.

a) Le brome 77 est un émetteur ß ^-.

b) L’expression de la constante radioactive est l= T ln2.

c) Le nombre initial de noyaux de brome 77 dans l’échantillon est égal à 1,8 × 10²¹.

d) L’énergie cinétique initiale de l’ensemble des particules émises a pour valeur 32 × 10⁶ J.

Dans une centrale nucléaire, une des réactions les plus courantes est la suivante :

²³⁵₉₂ U+ ₀¹n--> ⁹⁴₃₈ Sr + ¹⁴⁰_Z Xe + x ₀¹n

a) Les valeurs de x et de Z sont respectivement 2 et 52.

b) La valeur absolue du défaut de masse est égale à |Dm|=|m(⁹⁴₃₈ Sr) + m (¹⁴⁰_Z Xe)+ m( ₀¹n)- m(²³⁵₉₂ U)|

c) L’énergie libérée par la fission d’un noyau ²³⁵U est donnée par la relation : D E =|Dm| . c² dans laquelle .m s’exprime en kg, c s’exprime en m.s^-1 et .E en eV.

L’uranium 238 de la centrale peut, par capture d’un neutron rapide, donner un nouvel isotope : l’uranium 239. Ce dernier est radioactif et par suite d’émissions successives se transforme en plutonium 239 ²³⁹₉₄ Pu avec émission de particules X.

d) Les émissions X sont des émissions ß ^-.

Le montage ci-dessous comprend :un générateur idéal de tension E = 6 V, un conducteur ohmique de résistance R = 1 kW, un condensateur de capacité C initialement déchargé et un interrupteur K à deux positions. Y_A et Y_B sont les entrées d’une carte d’acquisition d’un ordinateur.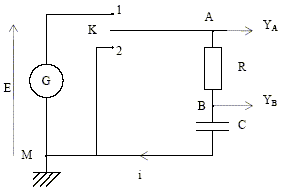

On bascule l’interrupteur K en position 1.

a) La voie Y_A détecte la tension aux bornes du conducteur ohmique.

b) En basculant l’interrupteur en position 1, le condensateur se charge.

c) La valeur de la tension en fin de charge aux bornes du condensateur est inférieure à 6 V.

d) A chaque instant l’intensité i(t) est donnée par la relation i(t) = u_AB(t) / R

On considère l’association en série d’une bobine sans noyau, d’inductance L = 400 mH et de résistance r, avec un conducteur ohmique de résistance R = 100 W La tension u aux bornes de l’association est telle que : - pour t < 0, u = 0 ; - pour t > 0, u = E = 15 V.

On obtient l’enregistrement de l’intensité i traversant le circuit, en fonction du temps :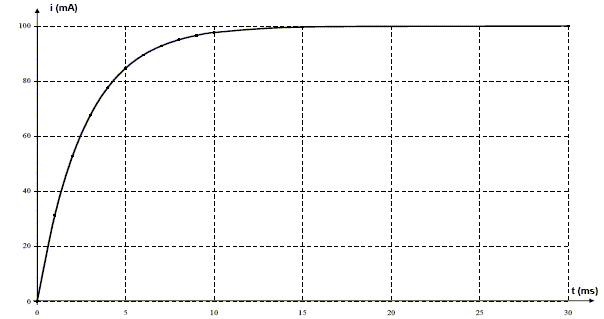

a ) Si la bobine contient un noyau de fer doux, l’intensité en régime permanent est plus faible.

b) L’intensité dans le circuit peut s’exprimer sous la forme suivante : i(t) = A exp(- a t) + B, avec A, B et a valeurs positives.

c) La résistance de la bobine est r = 50 W

d) La constante de temps du circuit est t = L/R.

On considère que le circuit électrique d’un appareil jetable avec flash incorporé est donné par le schéma ci-dessous.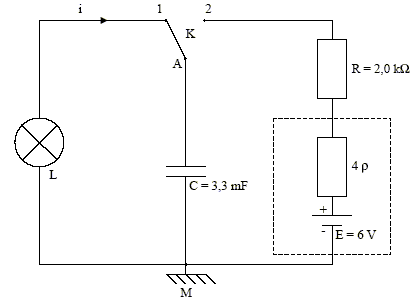

Ce circuit permet d’obtenir un éclair intense bien que l’alimentation soit constituée uniquement de 4 piles (LR₆) de 1,5 V chacune, en série.

Chaque pile a une résistance interne r= 0,15 W.

Les piles ne peuvent débiter une intensité supérieure à 500 mA sans être rapidement détériorées.

On considèrera que la lampe se comporte comme un conducteur ohmique de résistance r = 0,10 W.

Après avoir été en position 2 jusqu’à la charge complète du condensateur, le commutateur K est basculé en position 1.

Données : exp(-5) ˜ 6,7 × 10^-3 ; exp(-1) ˜ 0,37

a) La puissance la plus élevée fournie par l’alimentation au début de la charge est de 3 W.

b) Au bout d’une durée t = 5 t_c (avec t_c , constante de temps de la charge), le condensateur est chargé à plus de 99 %.

c) La constante de temps t_d de la décharge du condensateur est de 0,33 s.

d) Au bout du temps t = t_d , l’énergie restituée par le condensateur est W_e = ½CE².

On réalise le circuit ci-dessous (Figure 1), comprenant un générateur G de signaux triangulaires isolé de la masse, une résistance R et une bobine d’inductance L et de résistance négligeable par rapport à la résistance R. À l’aide d’une interface et d’un ordinateur, on visualise les variations de la tension u_BM en fonction du temps (Figure 2) :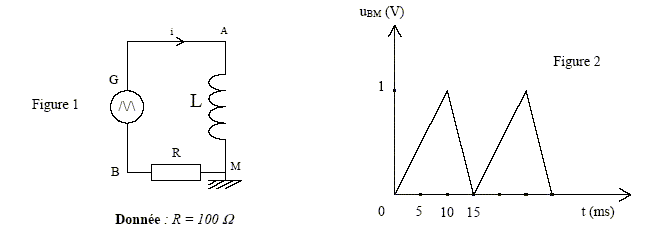

a) La tension aux bornes du conducteur ohmique a pour expression u_BM = Ri.

b) La tension aux bornes de la bobine a pour expression u_AM = Li.

Pour 0 < t < 10 ms, la tension u_AM relevée a pour valeur - 0,10 V.

c) L’inductance de la bobine a pour valeur L = 1 H.

d) La fréquence du signal vaut 50 Hz

Soit le schéma du montage ci-contre, comprenant une bobine d’inductance L et un condensateur de capacité C. L’interrupteur K est ouvert ; la tension aux bornes du condensateur U_AB = 10 V. On considère que la résistance de la bobine et des fils de connexion est nulle. A l’instant t = 0, on ferme l’interrupteur K. A l’aide d’un système informatique, des enregistrements ont été effectués et ont donné les expressions suivantes :

u_AB (t) = 10 cos (10³ t) avec u_AB (t) en volt, t en seconde ; i (t) = 10^-2 sin (10³ t) avec i (t) en ampère, t en seconde.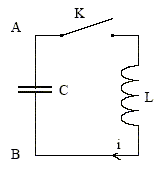

a) Les variations de u_AB et i au cours du temps correspondent à un régime pseudo-périodique.

b) Avec les conventions du schéma, on peut écrire i = C du_AB/dt

c) Le condensateur a une capacité C = 1µF.

d) L’énergie emmagasinée dans le circuit a pour valeur E = 50 µJ.

Une goutte d’eau, assimilée à une boule de rayon R, de masse m, de masse volumique r, tombe verticalement dans l’air. Elle est freinée dans sa chute par la force f= -6 p Rhv. ( v : vecteur vitesse de la goutte ; h : coefficient constant de viscosité). On a enregistré l’altitude z de la goutte en fonction du temps.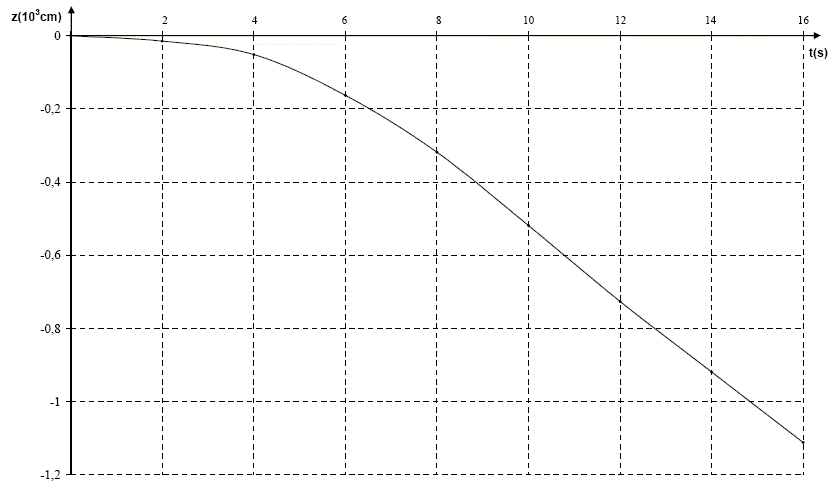

a) A partir de t = 8 secondes, le mouvement de la goutte est uniformément varié.

b) Le coefficient de viscosité h s’exprime en kg.m^-1.s^-1.

c) La valeur de la vitesse limite atteinte par la goutte est 1 m.s^-1.

d) La vitesse limite atteinte est inversement proportionnelle au rayon de la goutte.

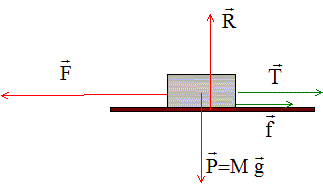
Un système constitué d’une locomotive et de ses deux wagons possède un mouvement non uniforme d’accélération a sur une voie rectiligne et horizontale.

Soient : M la masse de la locomotive, M = 80 tonnes ; m la masse de chaque wagon, m = 10 tonnes ;

Les vecteurs sont écrits en bleu et en gras

F : la force motrice développée par le moteur de la locomotive, F = 1,2 ×10⁵ N ;

f : la force de frottement dont la valeur est 200 newtons/tonne lors du mouvement ;

R : la réaction normale des rails sur le système {locomotive + deux wagons} ;

a : l’accélération du système ; g la valeur du champ de pesanteur.

a) Dans un référentiel terrestre, la deuxième loi de Newton appliquée au système {locomotive + deux wagons}, s’écrit :

b) L’accélération du centre d’inertie du système {locomotive + deux wagons} a pour valeur a = 1 m.s^-2.

c) La tension T subie par l’attelage qui relie la locomotive au premier wagon a pour valeur T = 24 kN.

La locomotive et le premier wagon sont reliés par un ressort de longueur à vide l₀ = 20 cm, de raideur k = 2,0 × 10⁵ N.m^-1.

d) la longueur du ressort est l = 20 cm.

Un avion volant horizontalement à une altitude h = 80 m avec une vitesse constante v₀ = 360 km.h^-1 laisse tomber une bouée en passant par la verticale d’un point A de la mer. La résistance de l’air ainsi que tous les frottements sont négligés. Donnée : valeur du champ de pesanteur g = 10 m.s^-2.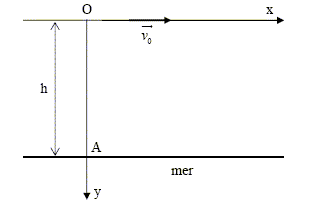

a) Les équations horaires du mouvement du centre d’inertie de la bouée projetées sur Ox et Oy

s’écrivent : x = 360 t ; y = 5 t². x et y exprimés en m et t en seconde.

b) La bouée touchera la surface de la mer au bout de 4 s.

c) La bouée tombe dans la mer à 1440 m du point A.

d) Entre le largage de la bouée et sa chute dans la mer, l’avion a parcouru une distance de 400 m.

On considère un satellite géostationnaire, assimilé à un point matériel de masse m. Le satellite se trouve à une altitude h = 36 × 10³ km prise par rapport au sol terrestre. Données : valeur du champ de pesanteur : g₀ = 10 m.s^-2 ; rayon de la Terre : R_T = 6 × 10³ km, masse du satellite : m = 40 kg.

a) Dans le référentiel géocentrique, la vitesse du satellite est nulle.

b) Le satellite gravite forcément dans le plan de l’écliptique contenant la Terre et le Soleil.

c) La troisième loi de Kepler appliquée au satellite s’écrit.

d) Le satellite subit un champ d’attraction de valeur approximative g(h) = 0,2 m.s^-2.

Soit un ressort à spires non jointives, de masse négligeable, et de raideur k = 20 N.m^-1. Le ressort est horizontal, une de ses extrémités A est fixe ; on accroche à son autre extrémité un solide S de masse m = 200g. Le solide S peut se déplacer sans frottement le long d’un axe horizontal Ox. A l’équilibre le centre d’inertie G du solide S coïncide avec l’origine du repère O.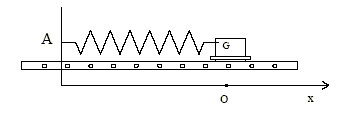

A un instant t = 0, on écarte le solide de sa position initiale vers la droite et on le lâche sans vitesse initiale.

a) La force exercée par le solide S sur le ressort est appelée « force de rappel ».

b) La solution de l’équation différentielle du mouvement du solide est de la forme :x(t) = X_max cos (wt) avec w ²=k/m, x(t) et X_MAX exprimés en mètres, t en seconde, k en N.m^-1 et m en kg.

On comprime maintenant le ressort en déplaçant le solide vers la gauche tel que OG = - 10 cm et on lâche le solide sans vitesse initiale à t = 0.

c) L’énergie mécanique, à t = 0, de cet oscillateur a pour valeur 0,2 J.

d) La vitesse maximale du centre d’inertie G du solide est de 1 m.s^-1.

Soit l’ion Lithium ⁷₃Li²⁺ , pour lequel les niveaux d’énergie possibles exprimés en électron-volt sont donnés par la relation E_n= -13,6Z²/n² , où Z est le numéro atomique de l’élément et n le niveau d’énergie. Données : 122,4×1,6 / 6,62 =30 ; 1 eV = 1,6 × 10^-19 J ;

Constante de Planck : h = 6,62 × 10^-34 J.s ; Célérité de la lumière : c = 3,0 × 10⁸ m.s^-1.

a) L’ion Lithium Li ²⁺ possède 1 électron.

b) L’énergie nécessaire pour arracher l’électron à l’ion est de 122,4 eV.

c) Pour passer du niveau fondamental au premier état excité, l’ion Lithium doit recevoir une énergie égale à 1/4 de l’énergie précédente.

d) Pour arracher un électron à l’ion, il faut un photon ayant une longueur d’onde égale à 10 nm.