|
QCM physique : durée 1 h ; 20 points.
- Un sonar, émetteur récepteur d'ondes ultrasonores, est
utilisé por cartographier les fonds marins. On admet que la vitesse v
de propagation de l'onde dans un liquide s'écrit v= [B/r]½ où B module de Bulk et r masse volumique du liquide sont des grandeurs
caractéristiques du liquide.
a) B peut s'exprimer en N s.
Un signal envoyé par le sonar est récupéré T0 secondes plus
tard ; l'eau de mer a pour grandeur caractéristiques B0 et r 0. La profondeur d'eau a pour
expression :
b) T0[B0/r0]½
c) 2T0[B0/r0]½
On mesure une même profondeur où l'eau a pour grandeurs
caractéristiques B= 1,05 B0 et r=
1,1r0. La durée T s'écoulant
entre l'émission et la réception du signal est telle que :
d) T<T0
e) T>T0
B=v²r : vitesse en m s-1
et masse volumique en kg m-3 : m2 s-2
kg m-3 soit kg s-2 m-1
Or N : kg m s-2 soit Ns : kg m s-1 a) est faux.
profondeur de l'eau : célérité * durée aller ( ou retour du signal)
soit ½ T0[B0/r0]½
b) et c) sont faux.
durée = 2 profondeur notée 2H / célérité soit T0= 2H [r0/B0]½ et T=
2H [1,1r0/(1,05B0)]½
;
T> T0 ; d) est faux. ; e) est vrai.
- a) Dans le vide toutes les ondes lumineuses ont la même
célérité
b) La fréquence d'une onde dépend du milieu traversé.
c) La longueur d'onde l d'une onde dépend
du milieu traversé.
Une onde monochromatique a une longueur d'onde l =
600 nm et une fréquence n= 5 1014
Hz dans le vide.Lorsqu'elle traverse un milieu d'indice n=1,5 :
d) Sa longueur d'onde reste égale à 600 nm.
e) Sa fréquence est égale à 3,3 1014 Hz.
a ) et c) vrais
La fréquence est une constante quel que soit le milieu
traversé.b ) et e) faux
La longueur d'onde l d'une
onde dépend du milieu traversé donc d) faux.
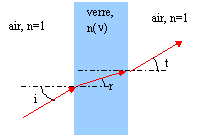
- Une onde lumineuse de longueur d'onde l
dans le vide traverse une lame de verre dont l'indice n dépend de l suivant la loi de Cauchy n= 1,619 + 0,0102/l² où l s'exprime en mm. Les fréquences des radiations violettes et
rouge dans l'air ( assimilé au vide) valent nviolet=
7,5 1014 Hz et nrouge=
3,75 1014 Hz. Quand i(lrouge)
= i(lviolet)
a) r(lrouge) >r(lviolet)
b) r(lrouge) <r(lviolet)
c) t(lrouge) >t(lviolet)
d) Dans le verre la lumière violette se propage moins vite que la
lumière rouge
e) Quelle que soit la longueur d'onde, i(l)=
t(l).
Dans la lame de verre, quelle que soit la longueur
d'onde, i(l)= t(l)
donc e) vrai ; c) faux
sin i = n sin r ; sin r = sin i / n ;lviolet<lrouge donc n violet
> n rouge donc r(lrouge)
>r(lviolet) a) vrai et b) faux
célérité dans le verre = c/ n ;
or n violet > n rouge donc v violet
<vrouge.d) vrai .
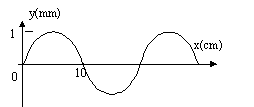
- Une onde de fréquence f= 0,1 kHz se propage de la gauche
vers la droite, le long d'une corde suposée infinie.La figure ci-dessus
représente l'allure de la corde à une date t=0 choisie comme origine
des temps.
a) L'onde est transversale.
b) Sa célérité vaut v= 2 mm/s
c) Sa longueur d'onde vaut l= 0,2 m
Pour le point O ( x=0), l'allure de y(t) correspond à la courbe :
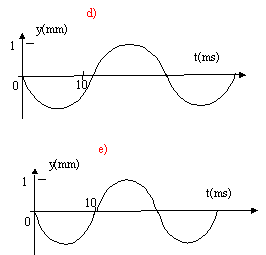
a) vrai
La longueur d'onde ( distance séparant deux crètes
consécutives) vaut 20 cm soit 0,2 m c) vrai
célérité v=l f = 0,2*100 =
20 m/s b) faux
période T= 1/f = 1/100 = 0,01 s
= 10 ms et non pas 11 ms, donc d) faux
Un point M quelconque de la
corde, situé à l'abscisse x, reproduit le mouvement de la source S avec
le retard x/v.
yS = A sin ( 2pf t) ; yM = A sin ( 2pf
(t-x/v)) = A sin (2pf t- 2px/l) soit yM (t=0)= A sin ( - 2px/l ) e) vrai
- Un mélange constitué de deux isotopes A Z
X et A' Z' X a une masse molaire M0.
On note respectivement M et M' les masses molaires des isotopes.
a) Z=Z'
b) A-Z= A'-Z'
la proportion de l'isotope A Z X est :
c) x= M/M0
d) x= (M0-M)/(M'-M)
e)x= (M'-M0)/(M'-M)
Deux isotopes ne différent que par leur nombre de
neutrons, donc a) vrai et b) faux.
proportion, notée x, de l'isotope A Z X et
notée 1-x pour A' Z' X
masse molaire M0 = xM + (1-x)M' ; M0= xM+M'-xM' ;
x = (M'-M0)/(M'-M)
donc ) vrai et c) et d) faux
- Le 1er, le 6, le 11 et le 16 mai 2003, max consomme à midi,
une même quantité d'un aliment contenant un élément radioactif X dont
l'activité A en fonction du temps est donnée ci-dessous. On suppose que
l'élément radioactif se fixe dans l'organisme. Le jour de sa
consommation, l'activité de cet aliment est 16 Bq. On prend ln2=0,7.
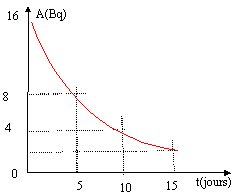
a) Le jour de sa consommation l'élément contient 114 (+ ou
- 1) noyaux.
Le 16 mai 2003 après midi, l'activité A16 mai de l'élément X
dans l'organisme de Max est :
b) 30 Bq
c) 8 Bq.
L'activité ½A16 mai sera atteinte
d) le 21 mai 2003
e) le 31 mai 2003.
D'après le graphe, la demi-vie est : t½= 5
jours. Or lt½=ln2 = 0,7 soit l = 0,7/5 = 0,14 jour-1.
A0= N0l soit N0=A0/l =16/0,14 =16*5/0,7 = 114,2 a) vrai.
Le 16 mai à 12+ heure : l'activité résiduelle, résultant de
la prise du 1er mai est : 16/ 23= 2 Bq ( entre le
1er et le 16 il y a trois demi-vie); l'activité résiduelle,
résultant de la prise du 6 mai est : 16/ 22= 4 Bq ( entre le
6 et le 16 il y a 2 demi-vie); l'activité résiduelle, résultant de la
prise du 11 mai est : 16/ 2= 8 Bq ( entre le11 et le 16 il y a une
demi-vie);
ajouter les 16 Bq de la prise du 16 mai à midi : total 30 Bq.b) vrai ; c) faux.
Le 21 mai ( une demi-vie plus tard) l'activité est 30/2 = 15 Bq d) vrai ; e) faux.
La charge élémentaire vaut 1,6 10-19 C et la
célérité de la lumière vaut 3 108 m/s.
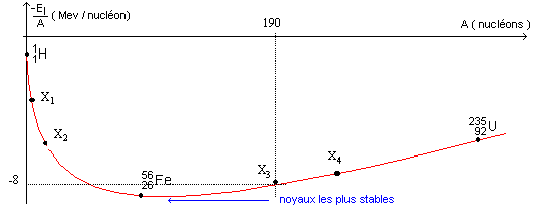
- a) X1 peut évoluer en X2 par fusion.
b) X4 peut évoluer en X3 par fusion.
c) l'énergie de liaison de X3 est 1,28 10-14 J.
Le défaut de masse de X3 est :
d) 0,142 10-30 kg.
e) 2,7 10-27 kg.
a) vrai et X4
peut évoluer en X3 par fission. b)faux .
l'énergie de liaison de X3 est : 8 *190 = 1520 MeV = 1520 106
eV =1520 106*1,6 10-19 = 2,4 10-10 J c)faux .
Le défaut de masse de X3 est El/c²= 2,4 10-10
/ 9 1016 = 2,7 10-27 kg.d)
faux ; e) vrai .
- On considère la réaction nucléaire suivante : 23592U
+ yxp-->9438Sr +14054Xe
+z yxp
x, y et z sont des entiers et yxpreprésente un
neutron. On donne les énergies de liaison (MeV) des noyaux :23592U
: 1760 ; 9438Sr : 800 ; 14054Xe
: 1150 ;
On note mU la masse du noyau d'uranium; NA le
nombre d'Avogadro ; ETEP, l'énergie libérée par 1 T.E.P (
tonne équivalent pétrole)
a) z=2.
b) la réaction est du type b-.
c) La réaction libère l'énergie E0= 190 MeV par noyau
d'uranium.
d) Il faut E/(E0NA) moles d'uranium 235 pour
libérer l'énergie E.
e) Il faut E0 /(mUETEP) tonnes de
pétrole pour libérer la même énergie qu'un noyau d'uranium 235.
conservation du nombre de nucléons (y= 1 pour un
neutron) : 235 + 1= 94+140+z ; z= 2 a) vrai
réaction de fission nucléaire b) faux.
La réaction libère l'énergie : 800+1150 - 1760+= 190 MeV par noyau
d'uranium. c) vrai
énergie libérée par une mole d'uranium 235 : E0NA
d) vrai
E0 /(mUETEP)
s'exprime en kg-1 donc ce n'est pas une masse e) faux.
- Le courant circulant à travers une bobine parfaite
d'inductance L évolue en fonction du temps t comme indiqué ci-dessous :
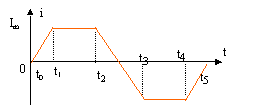
La tension UL(t) aux bornes de la bobine est de la forme :
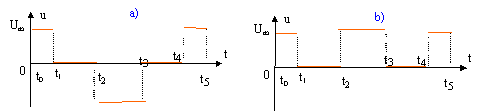
- c) entre t0 et t1 la bobine
fonctionne en mode générateur
d) entre t4 et t5 la bobine fonctionne en mode
générateur
e) L'énergie accumulée par la bobine de t0 à t1
vaut UmIm( t1-t0)/2.
tension aux bornes de la bobine
: U= Ldi/dt
entre t2 et t3 : di/dt est négative , L est
positive donc U<0 a )vrai ;b) faux.
entre t4 et t5 la bobine stocke de l'énergie et fonctionne en mode récepteur d) faux.
énergie stockée : dE= u i dt = L i di
puis intégrer de t0 à t1 : E= ½LI²m
Or i = kt ( k = constante) ; Um= Ldi/dt = Lk
; Im = kt1 ; t1 = t1-t0
car t0=0.
E= ½L( kt1)2=½Lk * kt1*t1 =
½UmIm( t1-t0) e )vrai
- La tension aux bornes d'un condensateur de capacité C, en
série avec une résistance R= 250 W, évolue
en fonction du temps comme indiqué ci-dessous.L'énergie accumulée par
le condensateur au bout d'un temps très long est de 1 mJ.
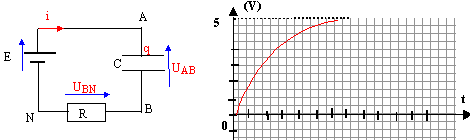
Le courant i est de la forme :
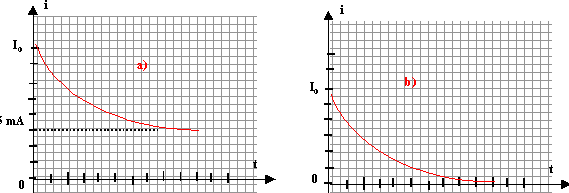
c) I0= 20 mA
d) C= 0,4 mF
e)C=80 m F
a) faux ; b) vrai
I0 = 5/ 250 = 0,02 A = 20 mA c) vrai
énergie stockée par le condensateur en fin de charge :
½CU²= 10-3 J ;
C= 10-3*2/U² =2 10-3 / 52 = 8 10-5
F = 80 m F e) vrai
; d) faux.
- Les courbes ci-dessous représentent les évolutions en
fonction du temps de l'énergie du condensateur C, initialement chargé,
et de l'énergie de la bobine supposée parfaite d'inductance L. Le
courant i est sinusoïdal avec une amplitude de 50 mA.
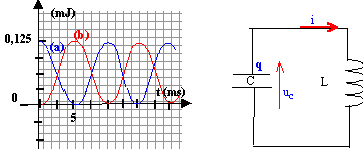
a) L'énergie totale du circuit vaut 0,25 mJ
b) L= 0,1 H
c) C= 1mF
La fréquence du courant i est :
d) 50 Hz
e) 100 Hz
L'énergie totale du circuit vaut 0,125 mJ a) faux.
Quand la bobine stocke toute l'énergie : 0,125 10-3 = ½LI²m
soit L= 0,25 10-3 /I²m= 0,25 10-3 /0,052
=0,1 H b)vrai.
période des courbes ci-dessus : 10 ms = 0,01 s ; période de
l'oscillateur LC= 0,02 s ; fréquence 1/0,02 = 50 Hz
d) vrai ; e) faux.
T= 2p(LC)½ soit C= T²/(4p²L)=
0,02²/(4*3,14²*0,1) = 10-4 F c)
faux.
- La courbe ci-dessous représente l'évolution du courant i(t)
circulant dans un circuit RLC série pendant une durée de 20 ms. On
donne C= 10 mF et p²=10.
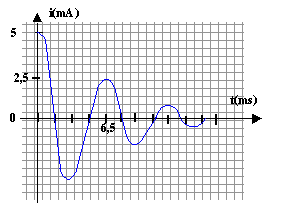
a) La pseudo-période T est légèrement supérieure à la
période propre du circuit
b) T est de l'ordre de 2p 10-3 s.
c) L est de l'ordre de 0,1 H
d) R<200 W
e) R>200 W
a) b) vrais
T= 2p(LC)½ soit L= T²/(4p²C)= 10-6/10-5
= 0,1 H c) vrai.
L'amortissement est d'autant plus grand que la résistance R est grande.
d) faux ; e) vrai
- A l'instant t=0, on lâche sans vitesse initiale une bille
pleine sphérique, de rayon R et de masse volumique r,
dans un fluide de masse volumique r '.
Outre son poids et la poussée d'Archimède, la bille est soumise à une
force de frottement fluide dt type -kv
où k est une constante et v le
vecteur vitesse à l'instant t. k dépend de la viscosité du fluide selon
k= 20hR.
La taille du récipient est suffisante pour obtenir l'évolution de la
vitesse v pendant 3 s. Cette vitesse est représentée ci dessous par la
courbe rouge dite de référence.
On reprend la même expérience avec des billes de rayon 2R et un fluide
de même masse volumique mais de viscosité 2h.
L'expérience (x,y) correspond à la chute d'une bille de rayon x dans un
fluide de viscosité y.
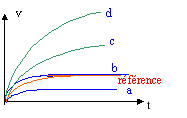
a) La courbe a correspond à l'expérience (R ; 2h)
b) La courbe b correspond à l'expérience (2R ; h)
c) La courbe c correspond à l'expérience (2R ; 2h)
d) La courbe d correspond à l'expérience (R ; 2h)
e) La courbe de référence correspond aussi à l'expérience (2R ; 2h)
La bille est soumise à son poids, verticale, vers le bas, valeur mg = r Vg = r 4/3 p R3 g
- à la poussée d'Archimède verticale, vers le haut, valeur r' Vg=r' 4/3 p R3 g
- à la force de frottement fluide, verticale, vers le haut, valeur 20hRv
Lorsque la vitesse limite est atteinte la valeur du
poids est égale à la somme des valeurs de la poussée d'Archimède et de
la force de frottement
mg=r g V = r '
g V + 20hRvlim avec V= 4/3 p R3.
vlim = 4/3 p R2g(r -r ')/ (20h)
La vitesse limite est proportionnelle au carré du rayon et inversement
proportionnelle à la viscosité.
La courbe a correspond à l'expérience (R ; 2h)
a) vrai
La courbe c correspond à l'expérience (2R ; 2h) c) vrai
- Un solide supposé ponctuel , de masse m= 100 g, est lancé
en O avec une vitesse horizontale initiale v0= 6 m/s. Il est
soumis à une force de frottement opposée au vecteur vitesse et dont
l'intensité varie selon le graphe :
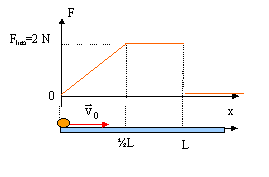
a) Le solide s'arrête en x= L = 1 m
b) La vitesse du solide en x= ½L vaut racine carrée (26) / 2 m/s.
c) La vitesse du solide en x= 0,25L vaut racine carrée (26) / 2 m/s.
d) Le solide garde une vitesse constante entre x= ½L et x= L
e) Le travail de F entre x=0 et x= L vaut -3 FlimL/4.
th de l'énergie cinétique entre 0 et L : ½mv²fin-½mv²0
= travail de la force de frottement ( - aire comprise entre la courbe
rouge et l'axe Ox)
travail de la force de frottement de x=0 à x=L : -½Flim ½L -
Flim ½L = - 3/4 Flim L e)
vrai
½mv²fin-½mv²0 = -3/4 Flim
L = -0,75 *2 = -1,5 J
½mv²fin= ½mv²0 -1,5 = 0,5*0,1*36-1,5 = 0,3 J a) faux
travail de la force de frottement de x=0 à x=0,25L :
-0,5 Flim*0,25L / 2 = -0,0625 FlimL= -0,125 J
½mv²0 =0,5*0,1*36 = 1,8 J ; ½mv² = 1,8-0,125 = 1,675 ; v² =
1,675*2/0,1 =33,5 c) faux .
travail de la force de frottement de x=0 à x=0,5L : - Flim*0,5L
/ 2 = -0,25 FlimL= -0,5 J
½mv²0 =0,5*0,1*36 = 1,8 J ; ½mv² = 1,8-0,5 = 1,3 ; v² =
1,3*2/0,1 =26 b) faux .
entre x= ½L et x= L, la bille n'est pas pseudo-isolée car la force de
frottement n'est pas nulle.d) faux
- S1 et S2 sont deux satellites d'un
astre A de masse M. Le satellite S1, de mase m1,
a une trajectoire circulaire uniforme de rayon R autour de A. Le
satellite S2 décrit une éllipse de demi grand axe a. On
donne M=1031 kg, m2 = 1023 kg, m1
= 1024 kg, R= 1,5 108 km, a= 9R/4 et G= 20/3 10-11
SI.
a) La vitesse de S1 vaut 2/3 105
m/s.
b) La période de révolution de S1 autour de A est environ104p/8 heures
c) La période de révolution de S2 autour de A est environ104p/8 jours
d) La vitesse de S2 a sa position la plus éloignée de A vaut
racine carrée (GM/a)
e) L'aire balayée par le rayon vecteur AS1 pendant une durée
donnée est égale à l'aire balayée par le rayon AS2 pendant
la même durée.
v² = GM/R= 20/3 10-11*1031/1,5
1011 = 2 1010/4,5= 20 1010/ 45 = 4/9 *
1010 ; v =2/3 105 m/s a)vrai
T² / R3 = 4p²/(GM )( 3è loi de Kepler)
T²= R3 4p²/(GM
)=(1,5 1011)34p²*3 1011/20 * 10-31
= 1,53*6 p² 1012=1,52*9p² 1012.
T= 1,5*3 p 106 s = 4,5 p 106/ 3600
heures = 4,5 p 104/ 36= p 104/ 8 heures b)vrai
T²2 / a3 = 4p²/(GM )
T²2= a3 4p²/(GM ) =
(9R/4)3 4p²/(GM ) soit T²2= (9/4)3T² ; T2
= 3,37 T c) faux
La vitesse de S2 a sa position la plus
éloignée de A vaut racine carrée (GM) / a d) faux
Le mouvement de chaque
planète est tel que le segment de droite reliant le soleil (
astre central) et la planète balaie des aires égales pendant des durées
égales.e) faux
- 1ère expérience : On lance de O, avec une
vitesse v0 faisant un angle a
avec l'horizontale une bille supposée ponctuelle. On note h1
la hauteur maximale atteinte par le projectile et p1 = OA la
portée. On néglige tout frottement.
2ème expérience :on effectue un lancer similaire avec
la même bille en gardant le même angle a mais
en doublant v0.
a) la hauteur maximale vaut 4 h1.
b) la portée vaut 4 p1.
3ème expérience : on effectue un autre lancer avec la
même bille en gardant la même vitesse v0 mais en doublant
l'angle a.
c) La hauteur maximale vaut 2 h1.
d) la portée vaut p1/2
e) La norme de la vitesse en A est indépendante de l'angle de lancement
a.
p1= v0² sin(2a)/g : si
la vitesse double et a= cte alors p1 quadruple a) vrai
-
h1= ½v0²
sin²a/g : si la vitesse double et a= cte
alors h1 quadruple b) vrai
si la v0= cte et si a double :
sin²a ne quadruple pas, ne double pas c) faux
si la v0=
cte et si a double : sin(2a) n'est pas divisé par 2 d) faux
La norme de la vitesse en A est indépendante de
l'angle de lancement a : appliquer le
théorème de l'énergie cinétique entre O et A ( le poids ne travaille
pas car les altitudes de O et A sont identiques)
en conséquence ½m v²O= ½m v²A et e) vrai
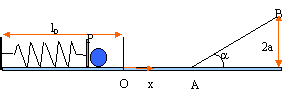
- A l'instant t=0, le ressort ( raideur k) est comprimé de a
par rapport à sa longueur à vide l0.Une masse m, placée
contre la plaque P, se trouve alors à l'abscisse -a. On libère le
dispositif sans vitesse initiale. On néglige les frottements. La masse
de la plaque est supposée très inférieure à m. On donne k/m= 10 et a=
1( dans le système MKS, mètre, kilogramme seconde) g= 10.
Dans le cas où la masse m reste constamment solidaire de la plaque P,
sa vitesse v à l'abscisse x est donnée par :
a) v²= k(a²-x²)/m.
Dans le cas où la masse m est simplement poussée par la plaque et libre
de se séparer de celle-ci, la séparation intervient quand :
b) x=0
c) x= +a
m rencontre un plan incliné d'un angle a=
30 ° par rapport à l'horizontale. Le point B se situe à une hauteur 2a
par rapport à l'horizontale.
d) La vitesse de m en A vaut 10 m/s.
e) m atteint B.
conservation de l'énergie mécanique:
au départ ( t=0) : énergie potentielle élastique ½ka²
à l'abscisse x ( solide au contact de P) : énergie potentielle
élastique + énergie cinétique ½kx²+½mv²
½kx²+½mv² = ½ka² ; v²= k/m(a²-x²) a) vrai
La bille se sépare de la plaque lorsque le ressort passe par sa
position d'équilibre O, alors x=0 b) vrai ;
c) faux
La vitesse de m en A est égale à la vitesse en O , car entre O et A le
solide est pseudo-isolé
½ka² = ½mv²A soit v²A=k/m a² = 10 et vA = 10 ½ d) faux
conservation de l'énergie mécanique entre A et B (
origine des altitudes A)
EA= ½mv²A ; EB= ½mv²B +mg 2a
½mv²A = ½mv²B +mg 2a ; v²A = v²B
+g 4a ; v²B= v²A- 4a g = 10 -40
un carré ne peut être négatif, donc B n'est pas atteint e) faux
- Une colonne de randonneurs avance en ligne droite avec une
vitesse constante de 7,2 km/h. Jule, le randonneur de tëte, se trouve
constamment à 100 m de Léon, le randonneur fermant la marche. Max doit
porter une bouteille d'eau à Jules de la part de Léon. Il court à une
vitesse constante vMax le long de la colonne en mouvement.
Lorsqu'il a remis la bouteille à Jules, il repart immédiatement vers
Léon, toujours à la même vitesse vMax . Quand il a rejoint
Léon, celui-ci a parcouru 100 m.
a) Max rattrape Jules 25 s après avoir quitté Léon
b) Jules parcourt 50 m pendant que Max remonte la
colonne de randonneurs de Léon à Jules.
c) Max rejoint Léon 50 s après avoir débuté
sa course.
d) Au total Max a parcouru 200 m.
e) La vitesse de Max est vMax
=2(1 + 2½) m/s.
7,2 km/h = 2 m/s ; Léon parcourt : 100 = 2 t soit t =
50 s ( durée de la course de Max) c) vrai
t1 : durée de l'aller ; t2 : durée du retour ; t1+
t2 = 50 (1)
distance parcourue à l'aller par : Max : d= vMax t1
; Jules : 2 t1 ; Max à 100 m de retard sur Jules :
vMax t1 = 100 + 2 t1(2)
au retour Max et Léon se déplace en sens contraire et sont initialement
distants de 100 m :
distance parcourue au retour par : Max : d= vMax t2
; Léon : 2 t2 ; Max à 100 m de retard sur Jules :
vMax t2 + 2 t2 = 100 (3)
(2) donne t1 = 100/(vMax-2)
; (3) donne t2 =100/(vMax+2)
; repport dans (1)
50 = 100/(vMax-2) + 100 / (vMax+2) ; v²Max-4
= 2[(vMax+2) +(vMax-2)] = 4vMax ; v²Max
- 4vMax -4 =0
la résolution donne :vMax =2(1+ racine carrée (2)) e) vrai
t1 = 100/(vMax-2) = 100 / (2 rac.carrée(
2)) = 50 / 2½= 35,4 s. a) faux
Jules parcourt 2 t1 =
70,8 m pendant que Max remonte la colonne b)
faux
Max parcourt : 50*vMax = 50*2(1+ racine
carrée (2)) = 241 m. d) faux
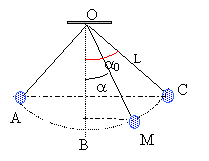
- Une masse m attachée à un fil inextensible, sans masse, de
longueur L, oscille dans un plan vertical entre les positions A et C.
g= 10 m/s²
On néglige tout frottement. On lâche m de C sans vitesse initiale et il
atteint A une seconde plus tard.
a) L= 25 cm
b) L= 1m
c) L'accélération de m est toujours normale à la trajectoire.
On ne néglige plus les frottements de l'air. Ils sont alors modélisés
par une force colinéaire à la vitesse, de sens contraire, de valeur fv
où f est un coefficient positif. Au bout de 10 aller retours, a vaut a 0/3
d) Le régime est apériodique.
e) La composante tangentielle de l'accélération vaut -fLa'/m.
période T= 2p(L/g)½
= 2 s soit L=T²g/(4p²) = 4*10 / 40 = 1 m b) vrai ; a) faux.
L'accélération de m est normale à la trajectoire si le
mouvement est circulaire uniforme ; ce qui n'est pas le cas ici.c) faux.
Le régime est pseuropériodique ( amortissement) d) faux
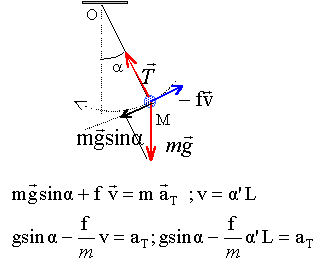 e)
faux e)
faux
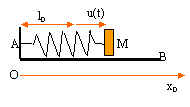
- Une plate forme AB a un mouvement périodique de période T,
parallèlement à Ox0 fixe par rapport à un observateur
terrestre. On installe à bord de cette plate forme un système
comportant un ressort de raideur k. L'une des extrémités est solidaire
d'une masse M assimilable à un point matériel et l'autre extrémité est
fixée en A. On note u(t) l'abscisse de M par rapport à la plate forme.
L'origine de u est la position d'équilibre de la masse. La masse M
subit une force de frottement F=-fv
colinéaire à sa vitesse par rapport à la plate forme.
On fait varier T et M acquiert un mouvement périodique de période T
a) Quelle que soit la valeur de T le système est à la résonance.
b) A la résonance T= (M/k)½.
c) A la résonance M est immobile par rapport à la plate forme.
d) Une résonance aigue correspond nécessairement à une fréquence de
résonance élevée.
e) La résonance est d'autant plus floue que f est élevé.
période propre du résonateur ( ressort + M) :T0
= 2p(M/k)½.
T période de l'excitateur (plate-forme)
A la résonance T=T0.a) et b) faux
Oscillations forcées : le résonateur oscille à la même période que
l'excitateur et paraît fixe par rapport à la plate-forme.
c) vrai.
Une résonance aigue correspond à un amortissement faible.d) faux ; e) vrai.
|













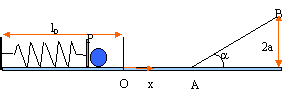

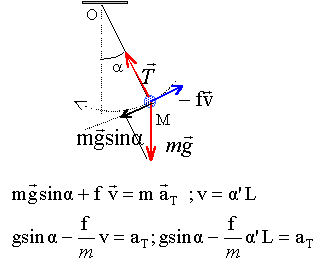 e)
faux
e)
faux
