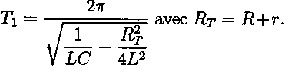|
Circuit LC ; lumière ; physique atomique ; oscillations d'un glaçon ; vibration d'une cuve physique : 2 h ; 4 exercices à traiter ; d'après concours Ecole Polytechnique Féminine 2005 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
On se propose d'étudier un capteur d'humidité. Etude du montage électrique : Un condensateur C est chargé à travers une résistance R0 = 100 W.En basculant l'interrupteur on décharge le condensateur dans une bobine (L= 100 mH, r) en série avec une résistance R. 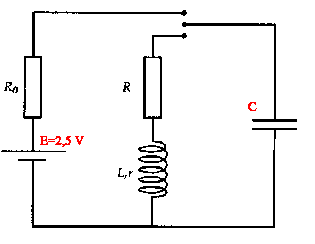
Etude du capteur d'humidité : Un capteur d'humidité comporte en particulier un condensateur dont la capacité C augmente lorsque le taux d'humidité t augmente suivant la relation : C= (0,4 t + 104,8) pF avec t en %. Ce capteur était inséré dans le circuit précédent. Quel est le taux d'humidité ? corrigé 2 p est sans dimension ; L inductance : E=½LI² soit L= 2 E / I² : énergie (joule ) / intensité ² (Ampère) ² ; J A-2. Or énergie (J) = tension (V) * intensité (A) * durée (s) d'où L : V A-1 s. C capacité : E=½CU² soit C = 2 E /u² : énergie / tension² soit V-1A s LC : s² donc racine carré (LC) en seconde. RT résistance (ohms) = tension (V) / intensité (A) soit V A-1. RT/L s'exprime en seconde.
1/(LC) = 4 p ²/ T1² + R²T/(4L²) ; 1/C= 4 p ²L/ T1² + R²T/(4L) C= [4 p ²L/ T1² + R²T/(4L)]-1. si RT=0 alors C= T1² / (4 p ²L) la capacité est fonction
linéaire de T1²
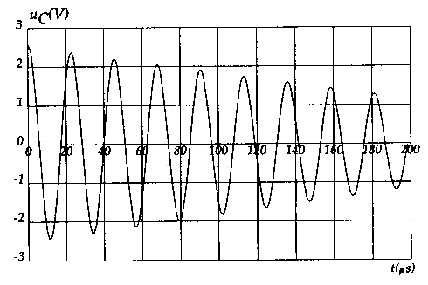
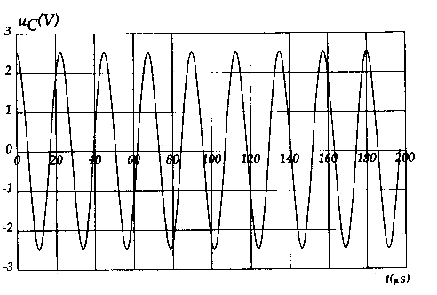
graphe 2 : la condition RT=0 est vérifiée car la tension uC n'est pas amortie ( l'amplitude reste constante) ; le montage avec amplificateur opérationnel compense à chaque instant les pertes d'énergie dans les résistances. 8 périodes correspondent à 180 ms soit T1 = 22,5 m s = 22,5 10-6 s. C=T1² / (4 p ²L) = (22,5 10-6)² / (4*3,14²*0,1)= 1,28 10-10 = 128 pF. C= 0,4 t+104,8 donne t = (C-104,8) / 0,4 =(128-104,8)/0,4 = 58%.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
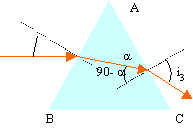
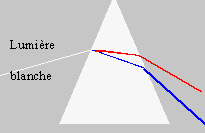
En utilisant un prisme, Newton a montré que la lumière blanche est polychromatique. Répondre par vrai ou faux en justifiant.
n= c/v = 3 108 / v soit v= 3 108/n donc la célérité dépend du milieu : la proposition 1 est fausse.
la proposition 2 est vraie.
longueur d'onde l(m) = célérité (m/s) fois fréquence (Hz) l 0 = 3 108 f dans l'air ; l = v f dans le verre du prisme l 0 /l = 3 108 / v = n ; l =l 0 / n dans l'air la longueur d'onde de la radiation est supérieure à la longueur d'onde de la même radiation dans le verre. la proposition 3 est vraie.
la proposition 4 est fausse.
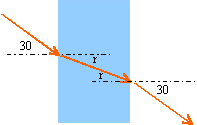
le faisceau incident ressort parallélement à lui même : il n'y a aps de dispersion la proposition 5 est fausse. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La notion de particules élémentaires est très ancienne ( Démocrite 460 - 370). L'atome est l'ultime élément de la division de la matière. La théorie moderne : ( 1970) La matière est représentée comme un assemblage de "briques" ( les 12 fermions), liées entre elles par les médiateurs de force ( les 14 bosons). Notre monde ordinaire, fait d'atomes, n'emploie qu'une partie de ce bestiaire : deux quarks ( up et down), qui s'assemblent par trois en un noyau. Ce noyau est environné de leptons- les électrons- pour former l'atome. Huit gluons collent les quarks entre eux, tandis que les photons lient les électrons au noyau par la force électromagnétique. Viennent ensuite les neutrinos électroniques n qui eux, interviennet dans les désintégrations radioactives, ainsi que les bosonsW-, W+ et Z0. Restent deux particules jamais encore observées, mais prédites par la théorie : le graviton, qui transmet la gravité, et le boson de Higgs, qui donne sa masse à toute particule. Selon le modèle standart, ce sont donc 18 particules qui rendent compte de notre matière classique. Mais si les quarks up et down, l'électron et le neutrino électronique, constituent notre "famille" de particules matèrielles ( matière stable), l'expérience prouve qu'il existe deux autres familles de particules. Instables, elles se désintègrent rapidement dans l'univers mais on peut les produire au laboratoire. Le bestiaire affiche donc 26 particules. Et ce n'est pas tout : à tous les fermions sont associés des anti-particules ( anti-quarks, anti-électrons, anti-neutrinos...) qui constituent l'antimatière ( elle aussi stable) ce qui multiplie leur nombre par deux. Au final, ce sont donc 38 particules élémentaires différentes que l'on peut aujourd'hui dénombrer. Particules de matière : les fermions .
corrigé Les particules constituant la matière : douze fermions liés par 14 bosons d'après le texte. Le proton n'est pas une particule élémentaire : le protons est constitué de 3 Quarks, collés par les Gluons. Charge d'un quark up : 2/3e ; down :-1/3 e Un proton est constitué de 2 Quarks up 1 Quark down : la charge totale du proton est + e. Un neutron est constitué de 1 Quark up 2 Quarks down : la charge totale du neutron est nulle 11 p +-->10 n + 01 e + 1 antineutrino "les neutrinos électroniques n qui eux, interviennet dans les désintégrations radioactives" Deux quark up coexistent : l'interaction forte maintient les quarks entre eux ; le gluon est le médiateur de l'interaction forte. "ce sont donc 18 particules qui rendent compte de notre matière classique" : Quarks up et down, électron, neutrino de l'électron, Huit gluons, photon, 3 Bosons, graviton et boson de Higgs. L'antimatière n'est pas de la science fiction : "l'expérience prouve qu'il existe deux autres familles de particules" l'antimatière est le miroir de la matière ; l'antimatière est stable. Les accélérateurs de particules du CERN sont capables de détecter le passage d'un quark : les quarks ont une charge et une masse et constituent la matière stable.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
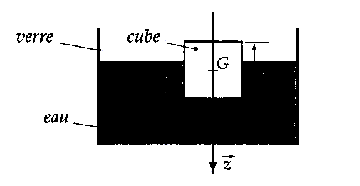
Soit un cube de glace d'arête a, de masse volumique rg= 0,9 g/mL, laissé à la surface de l'eau ( r eau = 1 g/mL). On rappelle que la poussée d'Archimède est dirrigée selon la verticale ascendante et est égale au poids du volume d'eau déplacé soit en valeur Parchi = -r eau Vimmergé g z. ( vecteurs écrits en gras et en bleu)
corrigé à l'équilibre le cube de glace est soumis à : son poids, vertical vers le bas , valeur mg =rg V g = rg a3 g et à la poussée d'Archimède, verticale, vers le haut, de valeur : r eau V immergé g à l'équilibre ces forces sont opposées et ont la même valeur : rg a3 g =r eau V immergé g V immergé =rg /r eaua3 Or V immergé = a2 zi ; zi = rg /r eaua l'origine de l'axe z est prise à la surface du liquide et zi représente la hauteur immergée. Les 9/10 èmes de la montagne
de glace sont immergés et restent invisibles, d'où le danger de
heurter.
mg- r eau V immergé g = mz" ; g = z" + r eau V immergé g / m avec V immergé = a2z et masse m = rg a3 g = z" +r eaua2zg/ rg a3 ; z" +r eau/(rg a)g z ; w02 =r eaug/(rg a) z" +w02 z= g (1)( éq. différentielle de l'oscillateur
harmonique sans amortissement)
z'= -a w0 sin (w0t) + bw0cos (w0t) z" = -aw02cos (w0t) -bw02sin (w0t) puis repport dans (1) :-aw02cos (w0t) -bw02sin (w0t) +w02 [rg/ r eau a + a cos (w0t) + b sin (w0t)] = g -aw02cos (w0t) -bw02sin (w0t) +aw02cos (w0t) +bw02sin (w0t)+ w02 rg/ r eau a = g w02 rg/ r eau
a =r eaug/(rg
a)rg/ r eau a =g ; d'où g= g : vérifiée
quelque soit t.
a = z0-rg/ r eau a. vitesse initiale nulle : z'(0) = 0 = -a w0
sin 0 + bw0cos 0 = bw0 ; w0
différent de zéro donc b =0.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Le système ci-dessous est constitué d'un tube cylindrique vertical ( section droite S, hauteur H) qui contient une colonne de liquide ( section droite S, hauteur H1). La partie supérieure du liquide est en contact avec l'atmosphère ( pression constante p0) Elle est limitée en bas par un piston de masse Ms qui agit dans la direction z. Le piston glisse sans frottement le long des parois du tube. Le fluide est supposé incompressible. 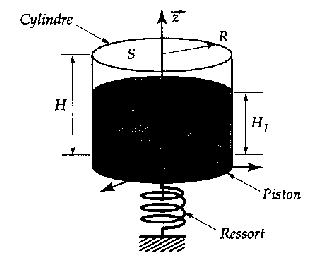 Quand une structure vibre au contact d'un fluide dense, en première approximation, on peut considérer que ce dernier vibre comme la structure.
A N : masse volumique du fluide r= 103 kg m-3 ; Ms= 2 103 g ; ks = 18 N/m ; R= 0,05 m ; H= 1 m et H1 = 0,5 m. corrigé 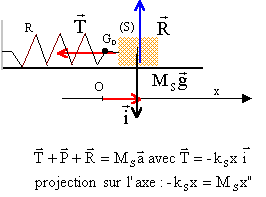
MS x" + kS x=0
soit x" + kS / MS x = 0 avec w12 =kS
/ MS = 18 / 2 = 9 ; w1
= 3 rad/s.
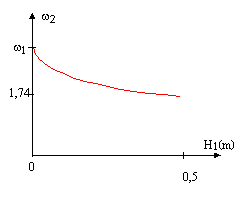
La masse du cylindre est supposée négligeable. w22 =kS / (MS + r SH1) avec S= p R² w22 = 18/(2+103*3,14*0,052*0,5)=3,04 ; w2=1,74 rad/s. 1/ w22 =MS /kS + r SH1/kS = 1/ w12 + r SH1/kS. fréquence f2 = w2 /(2p) = 1,74 /6,28 = 0,28 Hz.
Si la fréquence excitatrice est inférieure à w1, alors le système entre en résonance lorsque la fréquence de l'excitateur est égale à la fréquence propre du résonateur. Remarque : les valeurs numériques sont incohérentes ( raideur et Ms trop faibles par rapport à R= 0,5 m) : on a remplacé R par 0,05 m au lieu de 0,5 m.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||