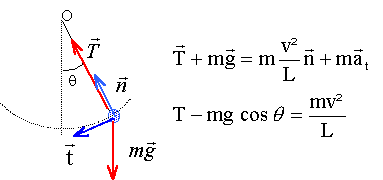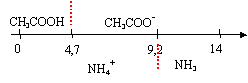|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||
| .
. |
|||||||||||||||||||||
|
|||||||||||||||||||||
|
|
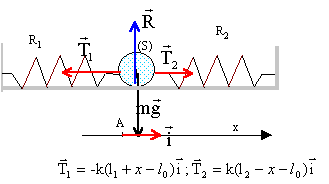
Un solide S de masse m, est fixée à deux ressorts R1 et R2 identiques, de longueur à vide l0 et de constante de raideur k. L'autre extrémité de chaque ressort est accrochée à un point fixe. Les deux ressorts sont portés par la même droite horizontale passant par le centre de la boule. On constate que les ressorts se sont allongés, par rapport à leur position à vide, d'une longueur notée L. On désigne par A la position du centre d'inertie G du solide lorsque l'ensemble est à l'équilibre. Les frottements sont négligeables. Ecarté de sa position d'équilibre, le solide est lâché sans vitesse initiale. Les deux resorts restent allongés au cours du mouvement. Au cours des oscillation, soit G une position quelconque du centre d'inertie du solide, telle que mesure algébrique (AG)= x >0. 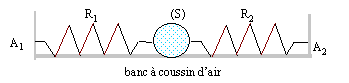
corrigé
longueur de R1 : l1+x = l0+L+x ; allongement : L+x longueur de R2 : l2-x = l0+ L-R-x ; allongement : L-x la seconde loi de Newton s'écrit en projection sur l'axe Ax : -T1 + T2 = mx" -k(L+x) + k(L-x)=mx" 2kx=mx" soit x" + 2k/m x=0 on pose w²= 2k/m ; w = 2pf soit f = 1/(2p)[2k/m]½ ; T= 1/f = 2p[2k/m]-½ solution du type : x(t) = Xmax cos( w t+j)
d'où Ec(x) = E(x)-Epe(x)=k( Xmax²-x²) dériver E(x) par rapport à x : 2kx x' + mv v'=0 avec x'= v et v'= x" ; 2kx v + mv x"=0 d'où en simplifiant par v : 2kx + mx"=0
E'pe(x)= ½kéqui x² d'où Ec(x) = E(x)-Epe(x)=k( Xmax²-x²)
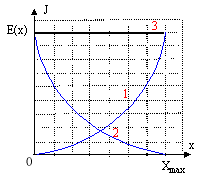
(1) énergie potentielle ; (2) énergie cinétique ; (3) énergie mécanique totale.
|
||||||||||||||||||||
|
Un pendule est constitué d'une masse m suspendue à un fil inextensible de longueur L. A partir de la position d'équilibre OA0, on communique à la masse m une vitesse horizontale de valeur v0. Une position quelconque est déterminée par son abscisse angulaire q. 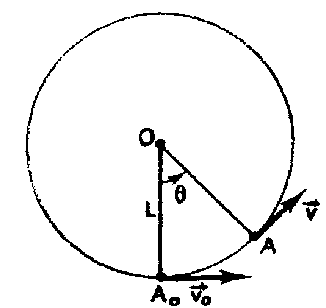
corrigé 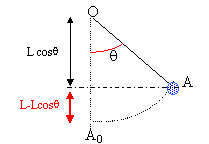
énergie mécanique ( A0 : origine de l'énergie potentielle de pesanteur) en A0 : E= ½mv0² en A : ½mv²+mgL(1-cosq) seul le poids traville, donc l'énergie mécanique se conserve : ½mv0² = ½mv²+mgL(1-cosq) v²= v0² -2gL(1-cosq)
T= m[g cos q +v²/L] = m[g cos q +v0²/L -2g(1-cosq)]= m[3g cos q +v0²/L -2g] La plus petite valeur de la tension Tmin est zéro : la petite masse m passe au point le plus haut (q= 180° et cos q = -1), le fil étant à la limite d'être tendu. d'où : 3g cos 180 +v0²/L -2g =0 |
|||||||||||||||||||||
|
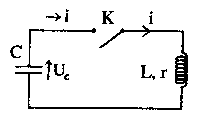
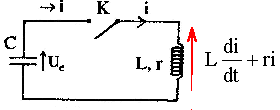
Le condensateur ci-dessus, de capacité C est initialement chargé sous une tension U0 A l'instant t=0, on ferme l'interrupteur K. A cet instant l'intensité i0 du courant est nulle. L'intensité du courant i(t) est comptée positivement quand le courant circule dans le sens indiqué ( courant de décharge du condensateur). On appelle q la charge de l'armature du condensateur.
corrigé i(t) = -dq(t) / dt = -q'(t) ; i'(t) = -q"(t) ( signe moins car décharge du condensateur) Cuc(t) = q(t) d'où q'(t) = C u'(t) et q"(t) = C u"c(t)
uc = Ldi/dt + ri ; uc = -Lq" - r q' ; uc = -LC u"c - rC u' ; LC u"c + rC u' + uc =0 si r négligeable alors LC u"c + uc =0 ou u"c +1/(LC) uc =0 on pose w0² = 1/(LC) ; w0 = 2pf ; T0 = 1/f = 2p/w0 =2p(LC)½. 2p est sans dimension ; u = Ldi/dt soit L= u dt/di : volt seconde ampère-1. C = q/u = It/u soit ampére seconde volt-1. LC a la dimension : seconde ² ; (LC)½ a la dimension : seconde. donc la période a bien la dimension d'un temps. solution de l'équation différentielle : uc= U0 cos(w0 t) à t=0, uc(0) = U0 ; i(t) = Cu'c= C U0w0( -sin(w0 t)) ; i(t=0 ) = 0 est bien vérifié. énergie stockée : dans le condensateur Ec= ½Cuc² ; dans la bobine : EL=½Li² Il y a un échange permanent d'énergie entre condensateur et bobine : en absence de résistance l'énergie totale est constante. lorsque le condensateur stocke toute l'énergie Etotale =½CU²0. lorsque la bobine stocke toute l'énergie : Etotale =½LI²max. d'où ½CU²0= ½LI²max ; I²max = CU²0 / L
|
|||||||||||||||||||||
|
couples : CH3COOH / CH3COO- pKa1 = 4,7 ; NH4+/NH3 pKa2 = 9,2 ; CH3 NH3+/CH3NH2 pKa3 = 10,7. log 2 = 0,3.
corrigé acide : espèce, ion ou molécule, susceptible de cédér un proton H+. Pour un acide fort pH= - log c ; dans ce cas pH= - log 10-2 = 2 or on trouve une valeur supérieure à 2 : donc l'acide éthanoïque est un acide faible. CH3COOH + H2O = CH3COO- + H3O+. Ka = [CH3COO-][ H3O+]
/ [CH3COOH]
donc l'ammoniac est une base plus faible que la méthylamine, à concentration égale.
à pH = 5 les espèces suivantes
prédominent : CH3COO-
et NH4+
n0(acide) = CA V'A = 10-2 * 10-2 = 10-4 mol.( réactif limitant) n0(méthyamine) = CB2 VB2 = 1,510-2 * 2 10-2 = 3 10-4 mol. CH3COOH + CH3NH2 = CH3COO- + CH3 NH3+. K = [CH3COO-][CH3 NH3+] / ([CH3COOH][ CH3NH2]) K = [CH3COO-][H3O+][CH3 NH3+] / ([CH3COOH][ CH3NH2][H3O+]) K = Ka1/Ka3 = 10-4,7 / 10-10,7 = 106 ; valeur grande, donc réaction totale dans le sens direct.
[CH3NH2]= 2 10-4 / 0,03 = 2/3 10-2 mol/L ; [CH3COO-]=[CH3 NH3+] = 10-4 / 0,03 = 1/3 10-2 mol/L. pH = pKa3 + log([CH3NH2]/[CH3 NH3+]) = 10,7 + log 2 = 11.
|
|||||||||||||||||||||
|
On considère la réaction d'oxydoréduction entre le métal cuivre et l'ion argent (I) : 2Ag+ + Cu(s) = Cu2+ + 2Ag(s). (1) La constante d'équilibre associée est K= 2 1015. On réalise deux expériences : - en mettant en contact direct les deux réactifs ; - en réalisant une pile électrochimique. A - réactifs directemment en contact :
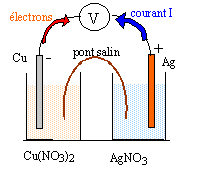
B -pile électrochimique : on dispose du matériel suivant : - Un bécher contenant contenant un volume V1=20 mL de solution de nitrate d'argent de concentration C1= 0,1 mol/L. - Un bécher contenant contenant un volume V2 = 20 mL de solution de nitrate de cuivre de concentration C2 = 0,05 mol/L. - Un fil de cuivre de masse m= 1,2 g et un fil d'argent. - Un pont salin contenant une solution ionique saturée de nitrate de potassium.
1 F voisin 105 C ; masse molaire Cu voisine 60 g/mol corrigé [Ag+]i =C1V1/(V1+V2)=0,1*20/40 = 0,05 mol/L ; [Cu2+]i =C2V2/(V1+V2)=0,05*20/40 = 0,025 mol/L Qi = [Cu2+]i /[Ag+]i 2=0,025 / 0,05²= 10. Qi <K donc évolution dans le sens direct. On observe un dépôt d'argent sur le fil de cuivre. K = [Cu2+]équi /[Ag+]équi 2 soit [Ag+]équi =([Cu2+]équi /K)½= (0,05/ 2 1015)½= 5 10-9 mol/L La transformation est totale.
à l'anode négative, oxydation du cuivre Cu(s) = Cu2+ + 2e-. à la cathode positive, réduction de l'ion argent : 2 Ag+ + 2e- = 2Ag(s) bilan : 2Ag+ + Cu(s) = Cu2+ + 2Ag(s) en accord avec le sens d'évolution spontané prévu ci-dessus. Le pont salin assure le contact électrique et permet aux solutions de rester électriquement neutres. Des ions Cu2+ apparaissent dans le bécher de gauche : donc migration des ions nitrate du pont vers ce bécher. Des ions Ag+ disparaissent
dans le bécher de droite : donc migration des ions K+ du
pont vers ce bécher.
xmax = 10-3 mol =1,9 10-2 mol = 2 10-3 mol [Cu2+]fin= 2 10-3 / 0,02 = 0,1 mol/L Qté de matière d'électrons = Qté de matière d'ion argent = 2 10-3 mol La charge d'une mole d'électrons vaut, en valeur absolue, 105 C ou 1 faraday. Qté d'électricité : 2 10-3 * 105 = 200 C
|
|||||||||||||||||||||
|
|