Aurelie 5/5

Condensateur et dipole RC ; nacelle en rotation ; projectile, joueur de tennis.

d'après concours 2005

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


nacelles en rotation

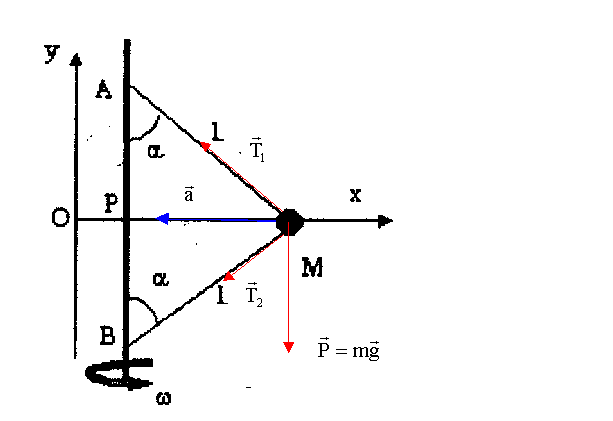
Un manège est constitué d'un axe vertical en rotation. Plusieurs nacelles sont suspendues par des tiges de longueur L= 5 m qui sont articulées au sommet A de l'axe. On néglige la masse de ces tiges. Pour des raisons de sécurité, un fil également de masse négligeable et de longueur L relie chacune des nacelles à la base B de l'axe de rotation. AB= 8 m.

Un enfant monte dans la nacelle. On considère l'ensemble de la nacelle et de l'enfant comme un point matériel M de masse m= 40 kg. La tige et le fil lorsqu'il est tendu font avec l'axe de rotation un angle a. g= 10 m/s².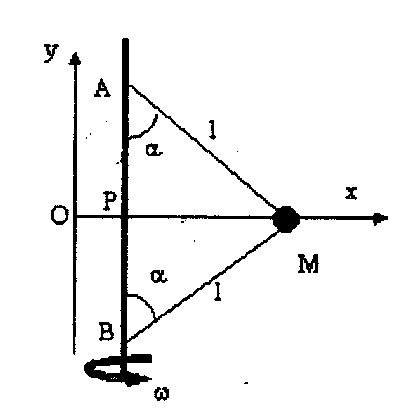

  1. Par des considérations géométriques calculer sina et cosa.
  2. L'axe tourne à vitesse angulaire constante w et le fil MB est tendu.
    - Porter sur le schéma la direction et le sens des différentes forces s'exerçant sur M. faire de même pour le vecteur accélération.
    - En utilisant les axes Ox et Oy déterminer en fonction de m, g, L, a et w les intensités T1 et T2 des forces exercées sur la tige et sur le fil.
    - Faire l'application numérique si l'axe de rotation fait ½ tour par seconde.
    - Déterminer la vitesse angulaire minimum à partir de laquelle le fil commence à se tendre.
corrigé
cos a = PB/L= AB/(2L) =8/10 = 0,8 ; sin² a= 1-cos²a= 1-0,8²= 0,36 ; sin a = 0,6.

l'accélération est centripète si la vitesse angulaire est constante.

écrire la seconde loi de Newton sur les deux axes :

sur Oy, l'accélération est nulle : T1 cos a - T2 cos a -mg =0.

T1-T2=mg / cos a (1)

sur Ox l'accélération vaut w² PM = w² L sin a: -T1 sin a - T2 sin a = - mw² L sin a

T1 + T2 = mw² L (2) ajouter (1) et (2) : 2 T1 = m( w² L+g / cos a)

T1 = ½ m( w² L+g / cos a) ; T2 = mw² L- T1 =½m( w² L-g / cos a)

l'axe de rotation fait ½ tour par seconde soit w=p radian par seconde

T1 = ½ m( w² L+g / cos a) =0,5*40 ( 3,14²*5+10/0,8)=1236 N.

T2 =½m( w² L-g / cos a) = 0,5*40(3,14²*5-10/0,8)= 736 N.

lorsque le fil n'est pas tendu, la tension T2 est nulle. A la limite : T2 =½m( w² L-g / cos alimite)=0

soit w²mini L-g / cos a=0 ; w²mini = g/(Lcos a)= 10/(5*0,8)=2,5 et wmini = 1,58 rad/s..


projectile

Un joueur de tennis est situé en A à la distance D= 9 m du filet et tente de lober son adversaire situé en B à une distance d= 2 m du filet. Le joueur frappe la balle à une hauteur h=0,5 m du sol avec un angle de tir a = 60° et une vitesse v0= 43,2 km/h. On assimile la balle à un point matériel de masse m= 60 g. g= 10 m/s² ; les frottements sont négligés.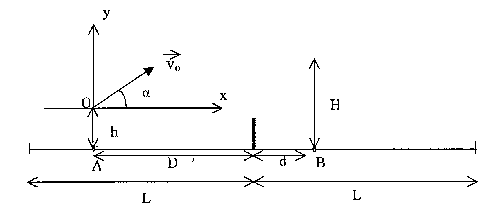

  1. Quelle est l'énergie cinétique de la balle au moment où elle quitte la raquette ?56 ; 0,36 ; 360 ; 4320 ; 4,32 ; 3,6 ; 5,6 J
  2. Quelles sont les affirmations suivantes qui sont vraies ?
    -a La balle de tennis a un mouvement de chute libre.
    -b Le vecteur accélération du centre d'inertie de la balle est égal au poids de la balle.
    -c Le mouvement de la projection du centre d'inertie de la balle suivant l'axe horizontal Ox est uniformément varié.
    a: seule ; b : seule ; c :seule ; a et b ; a et c ; b et c ; toutes; aucune.
  3. Quelle est l'altitude maximale de la balle par rapport au sol ? 7 ; 5,4 ; 12 ; 5 ; 11,5 ; 11 ; 6,4 ; 5,9 m.
  4. Combien de temps met la balle pour atteindre la hauteur maximale ?1,4 ; 1,2 ; 0,64 ; 2,06 ; 1,04 ; 2,24 ; 0,26 ; 1,64 s.
  5. Quelle est l'altitude de la balle par rapport au sol lorsqu'elle passe juste au dessus de B ? 2,07 ; 2,75 ; 3,07 ; 1,75 ; 3,75 ; 0,75 ; 1,07 ; 7,05 m
  6. A quelle distance du point A se situe le premier point d'impact au sol ? 12,05 ; 12,75 ; 11,57 ; 22,75 ; 5,75 ; 6,57 ; 24,75 ; 26,85 m.
  7. Sachant que la longueur totale du terrain et 2L= 24 m, quelle est la vitesse maximale que le joueur A peut donner à la balle pour quelle retombe à coup sur dans le terrain, l'angle restant le même ? 11,13 ; 11,81 ; 12,52 ; 14,38 ; 15,47 ; 16,23 ; 16,84 ; 17,62 m/s.
corrigé
énergie cinétique de la balle au moment où elle quitte la raquette : ½mv²

avec m= 0,06 kg et v0 = 43,2/3,6 = 12 m/s ; Ec= 0,5*0,06*12² = 4,32 J.

a) La balle de tennis a un mouvement de chute libre.
b) Le vecteur accélération du centre d'inertie de la balle est égal à g.
c) Le mouvement de la projection du centre d'inertie de la balle suivant l'axe horizontal Ox est uniforme.
a: seule.

accélération : ( 0 ; -g) soit (0 ; -10)

vitesse initiale (v0cos a ; v0 sin a ) soit (6 ; 10,39)

vitesse : v0cos a ; -gt +v0 sin a ) soit (6 ; -10 t+10,39)

position : x= v0cos a t = 6 t ; y = -½gt² + v0 sin a t = -5t²+10,39 t

trajectoire : y= -½gx²/(v0cosa)² + x tan a = -0,139 x² + 1,732 x.

au sommet de la trajectoire la vitesse est horizontale : -10 t+10,39 = 0 soit t = 1,039 s.

y= -5*1,039²+ 10,39 *1,039 = 5,4

ajouter 0,5 m soit 5,9 m au dessus du sol.

altitude de la balle par rapport au sol lorsqu'elle passe juste au dessus de B :

B est situé à 11 m de A : y = -0,139*11²+1,732 *11 =2,25 m

soit par rapport au sol 2,25 + 0,5 = 2,75 m.

premier point d'impact au sol y = -0,5 m

résoudre : -0,5 = -0,139 x² + 1,732 x.

x= 12,75 m.

vitesse maximale que le joueur A peut donner à la balle pour quelle retombe à coup sur dans le terrain :

x = 9+12 = 21 m ; y= -0,5 m

y= -½gx²/(v0cosa)² + x tan a = -20x² /v²0+ 1,732 x

v²0= 20 /(1,732x-y) = 20 x² /(1,732*21-(-0,5))= 239,2 soit v0 = 15,47 m/s.

condensateur et dipôle RC ( 6,5 pts)

On considère le circuit ci-dessous comportant un génrateur de tension constante E, un résistor de résistance R, un condensateur de capacité C et un interrupteur K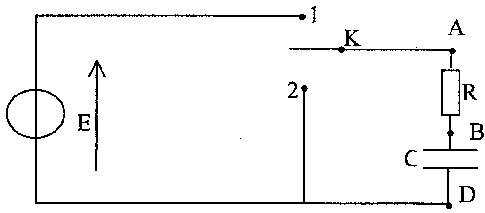

 

  1. L'interrupteur est en position 1.
    - En précisant les conventions utilisées, établir l'équation différentielle de la charge du condensateur.
    - Vérifier que la fonction uBD=A+Bexp(-bt) est solution de l'équation précédente quelque soit t si l'on choisit convenablement les constantes b et A.
    - Le condensateur est préalablement déchargé, on ferme le circuit en basculant l'interrupteur en position 1 à la date t=0. Quelle est à cet instant la valeur de la tension uBD ?
    - Déterminer l'expression de uBD en fonction des caractéristiques du circuit.
    - Qu'appelle-t-on constante de temps t du dipole RC ? Que représente-telle ? Calculer sa valeur.
    - Donner l'allure de la courbe uBD= f(t) que l'on pourrait visualiser à l'aide d'un oscilloscope à mémoire.
  2. Lorsque le condensateur est chargé, à une date choisie comme nouvelle origine des temps, on bascule l'interrupteur en position 2.
    - Sous quelle forme l'énergie emmagasinée dans le condensateur est-elle dissipée.
    - Déterminer sa valeur.
    E= 6,0 V ; R= 10 kW ; C= 100 nF.
 
corrigé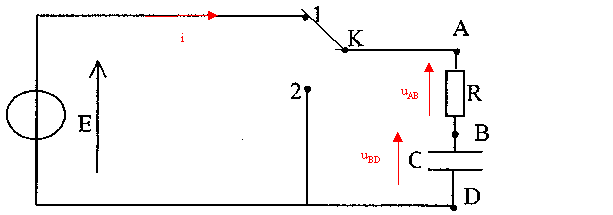

 

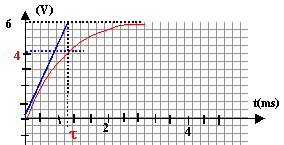
uBD+uAB= E avec uAB= Ri et i = dqB/dt.

or CuBD=qB soit i = dqB/dt = C duBD/dt = CuBD'.

uBD+ Ri = E ; uBD+ RCuBD' = E.

uBD=A+Bexp(-bt) ; dériver par rapport au temps: uBD' = -Bbexp(-bt)

repport dans l'équation différentielle :A+Bexp(-bt) + RC(-Bbexp(-bt)) = E

A + B(1-RCb)exp(-bt) = E

d'où par identification A= E ; 1-RCb=0 soit b = 1/(RC)

de plus à la date t=0 le condensateur est déchargé soit uBD=A+Bexp(-bt)=0

d'où 0=A+B soirt B= -A

uBD=E(1-exp(-t/ (RC)) .

constante de temps t du dipole RC : t = RC = 104*100 10-9 = 10-3 s.

au bout d'une durée supérieure à 5 t, le condensateur peut être considéré comme chargé : la constante de temps permet d'estimer la durée de la charge.

l'énergie emmagasinée dans le condensateur est dissipée sous forme d'énergie thermique (effet joule) dans le résistor

E= ½CE² = 0,5 * 100 10-9 * 6² = 1,8 10-6 J.



retour -menu