Aurélie 02/05

Ressorts ; oscillateur ; électricité ; optique ; acide fluorhydrique ; ester

physique : 1 h ; chimie : ½ h ; sans calculatrice ; d'après concours kiné CEERRF 2005

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


Mécanique ( 16 points)

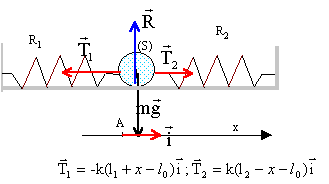
A Deux ressorts valent mieux qu'un : une boule de rayon R= 5,5 cm et de masse m, est fixée à deux ressorts R1 et R2 identiques, de longueur à vide l0= 25 cm et de constante de raideur k. L'autre extrémité de chque ressort est accrochée à un point fixe. Les deux ressorts sont portés par la même droite horizontale passant par le centre de la boule. On pose A1A2 = L et on note l1 et l2 les longueurs respectives de R1 et R2.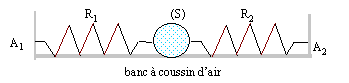

 

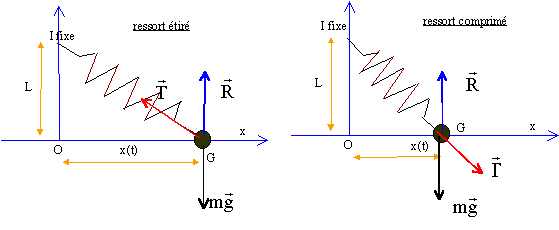
  1. En justifiant, déterminer à l'équilibre, la position A par rapport à A1 et A2, de G, centre d'inertie de la boule.
  2. Calculer A1A et A2A sachant que L= 75 cm.
  3. La boule peut glisser sur son support horizontal. On écarte celle-ci de sa position d'équilibre de 2 cm vers A2. A cet instant t=0, on lâche la boule, sans vitesse initiale, du point A3 ( AA3= 2 cm). Faire le bilan des forces qui agissent sur la boule entre A et A3, à l'aide d'un schéma clair.
  4. Exprimer les longueur l1 et l2 des ressorts en fonction de L, R, et x= mesure algébrique (AG)
    - En déduire l'expression des vecteurs tensions des ressorts en fonction de K, L, x , R et l0. ( on notera vecteur i, le vecteur unitaire de l'axe Ax)
    - A partir de la seconde loi de Newton, déterminer l'équation différentielle du mouvement de la boule.
    - Donner l'expression littérale de la période et de la fréquence du mouvement de la boule.

B Equilibre d'un oscillateur :Un solide s de masse m peut se déplacer, sans frottement, le long d'une tige horizontale T. Un ressort élastique, à spires non jointives, de constante de raideur k et de longueur au repos l0 = 10 cm est accroché au solide S de centre d'inertie G. La deuxième extrémité du ressort est accrochée au point fixe I. On pose IO= L= 6 cm ; IG= l et x= abscisse de G.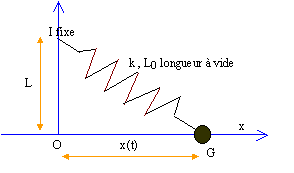

  1. Faire le bilan des forces appliquées au solide S. Pour cela on dessinera deux schémas clairs correspondant à deux situations que l'on précisera.
  2. En choisissant comme niveau de référence Ep=0, exprimer l'énergie potentielle du système {solide+ ressort} en fonction de k, l0, L et x.
  3. En déduire les positions d'équilibre du système, correspondant aux valeurs minimales de l'énergie potentielle. Faire l'application numérique.
corrigé
Les deux ressorts étant identiques : l1=l2.

l1+l2+ 2R= L ; A1A = A2A = l1+ R = ½L = 37,5 cm.

longueur de R1 : l1+x = ½L-R+x

longueur de R2 : l2-x = ½L-R-x

la seconde loi de Newton s'écrit en projection sur l'axe Ax : -T1 + T2 = mx"

-k(½L-R+x-l0) + k(½L-R-x-l0)=mx"

2kx=mx" soit x" + 2k/m x=0

on pose w²= 2k/m ; w = 2pf soit f = 1/(2p)[2k/m]½ ; T= 1/f = 2p[2k/m]-½

Ep= ½k(l-l0)² avec l²= L²+x² soit l= [L²+x²]½.

Ep= ½k( [L²+x²]½-l0)²

dériver Ep par rapport à x : E'p =k[( [L²+x²]½-l0)x [L²+x²]-½

la dérivée s'annule pour x=0 et [L²+x²]½= l0 soit x = [l0²-L²]½ et x = -[l0²-L²]½

x= 0 correspond à un maximum de l'énergie potentielle ( le ressort est comprimé et si on l'écarte de cette position il s'en éloigne : équilibre instable)

x = [l0²-L²]½ et x = -[l0²-L²]½ correspondent à des minimas de l'énergie potentielle ( si on écarte le ressort de ces positions il y revient : équilibre stable)

x = [l0²-L²]½= [100 - 36]½ = 8 cm


électricité : 12 points

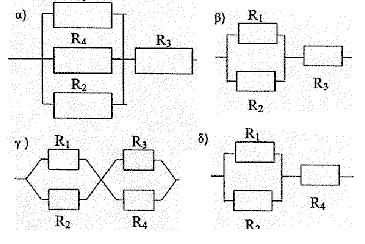
Un générateur idéal de tension E= 12 V alimente le pont ci-dessous :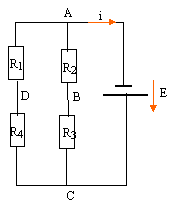

R1 = 20 ohms ; R2 = 5 W ; R3 = 15 W ; R4 = 60 W

  1. Calculer la résistance équivalente à l'ensemble.
  2. Calculer l'intensité I du courant débité par le générateur.
  3. Calculer l'intensité I1 du courant dans la branche ADC.
  4. Calculer la tension aux bornes de R1 puis de R2.
  5. Comparer les puissances consommées dans les branches ABC et ADC. Quelle loi de conservation vérifient-elles ?
  6. Quelle indication pourrait-on lire sur un voltmètre placé ente B et D ?
  7. Que se passerait-il si on reliait B et D par un fil conducteur ? Justifier les réponses à choisir parmi les propositions suivantes.
    - La résistance R4 serait court-circuitée et I1 traverserait DB.
    - La résistance R3 serait court-circuitée et I2 traverserait BD
    - Aucun courant ne traverserait BD et la résistance équivalente serait la même.
    - Aucun courant ne traverserait BD et la résistance équivalente de l'ensemble serait égale à 18,75 ohms.
    - L'ensemble AC est équivalent à :
corrigé
R2 et R3 en série équivalentes à R5 = R2+R3 = 20 W.

R1 et R4 en série équivalentes à R6 = R1+R4 = 80 W.

R5 et R6 en série équivalentes à Réqui = R5R6/ (R5+R6 )= 16 W.

I= E/Réqui = 12 / 16 = 0,75 A

courant dans la branche ADC : I1 = E/R6 = 12/80 = 0,15 A

courant dans la branche ABC : I2 = E/R5 = 12/20 = 0,6 A

tension aux bornes de R1 : UAD= R1I1 = 20*0,15 = 3 V

tension aux bornes de R2 : UAB= R2I2 = 5*0,6 = 3 V

Puissances : branche ADC : E I1 = 12*0,15 = 1,8 W ; autre branche : E I2 = 12*0,6 = 7,2 W

branche principale : E I = 12* 0,75 = 9 W

la puissance fournie par le générateur est égale à la somme des puissances consommées par les résistors.

UBD = UBA+UAD= - UAB +UAD= -3 +3 = 0 V

en conséquence la présence d'un fil entre B et D ne change pas la résistance équivalente, car ce fil n'est traversé par aucun courant.

l'ensemble des résistances est équivalent au schéma g: R1 et R2 en dérivation ; R3 et R4 en dérivation ;

optique : 12 points

 

On considère un objet Ab transversal et un écran fixe E et distants de D sur un banc d'optique. On cherche à déterminer les positions d'une lentille convergente mince, située entre l'objet et l'écran, permettant de visualiser une image nette A'B' sur ce dernier. On note O le centre optique de la lentille L et f' sa distance focale image. On pose AO= x ( on écrit en bleu et en gras les mesures algébriques).

  1. Faire un schéma clair de la situation.
  2. Exprimer en justifiant la distance OA' en fonction de x et D.
  3. A partir de la relation de conjugaison de Descartes, déterminer l'équation du second degré du type ax²+bx+c=0, en précisant les coefficients a, b, c.
  4. En déduire la condition sur D et f' permettant d'obtenir les deux solutions x et x' de l'équation précédente, correspondant à deux positions de la lentille donnant une image nette sur E.
  5. Exprimer les deux solutions en fonction de D et f'.
  6. En déduire l'expression de f' en fonction de D et d: distance entre les deux positions de la lentille.
corrigé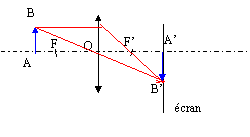

AO + OA' = D ; OA' = D - AO + = D-x

1/f' = 1/ OA' - 1/OA soit : 1/ OA' =1/f' + 1/OA = 1/f' - 1/AO = 1/f'-1/x

1/ OA' =( x-f')/ xf' soit OA' = xf'/ (x-f') = D-x

xf' = (D-x)(x-f') soit : x²-Dx + f'D=0 5 a=1 ; b= -D et c= f'D]

discriminant D = b²-4ac = D²-4f'D

il y a deux solutions si D est positif soit D>4f'.

x1 = ½[D+ ( D²-4f'D)½] ; x2 = ½[D- ( D²-4f'D)½] ; d = x1 -x2 = ( D²-4f'D)½

d² = D²-4f'D ; f' = (D²-d²)/ (4 D)

acide fluorhydrique : 10 points

 

On détermine la conductivité de deux solutions d'acide fluorhydrique de concnetrations différentes : S1 : 10-2 mol/L et s = 9 10-2 S/m ; S2 : 10-4 mol/L et s = 3,6 10-3 S/m.

  1. Décrire le mode opératoire, en précisant le matériel utilisé, pour préparer 1 L de la solution S2 à partir de S1.
  2. Ecrire la réaction du fluorure d'hydrogène HF avec l'eau.
  3. Calculer les concentrations des ions présents dans chaque solution.
  4. Déterminer les avancements volumiques finaux pour chaque solution. La réaction est-elle totale, limitée ? Justifier.
  5. Comparer le taux d'avancement de chaque solution et conclure.

Conductivité molaire ionique en S m² mol-1 : lH3O+ = 3,5 10-2 ; lF- = 5 10-3 .

corrigé
facteur de dilution : 100

prélever 10 mL de S1 à la pipette jaugée + pipeteur

placer dans une fiole jaugée de 1 L et compléter avec de l'eau distillée jusqu'au trait de jauge

agiter pour rendre homogène.

HF + H2O = F- + H3O+.

s = lH3O+ [H3O+] + lF- [ F-] avec [ F-] = [H3O+] = C mol m-3.

C= s /( lH3O++ lF- )= 9 10-2 /( (3,5 + 0,5)10-2 ) = 2,25 mol m-3 = 2,25 10-3 mol/L

pour S2 on trouve : 3,6 10-3 /( (3,5 + 0,5)10-2 ) = 0,09 mol m-3 = 9 10-5 mol/L

taux d'avancement volumique final : concentration / [H3O+] = 2,25 10-3/ 10-2 =0,225 pour S1 ( réaction limitée)

pour S2 on trouve : 9 10-5/ 10-4 =0,9 réaction presque totale

par dilution on déplace l'équilibre dans le sens direct, ionisation de HF.

ester : 10 points

 

  1. Ecrire l'équation de la réaction de synthèse de l'éthanoate de propyle en utilisant les formules semi-développées à partir de l'acide puis à partir d'un anhydride d'acide.
  2. On mélange 30 mL d'alcool avec 20,4 mL de l'anhydride d'acide. Quelle quantité de matière d'ester va-t-il se former ?
    alcool : masse volumique 0,8 g/mL et masse molaire 60 g/mol ; anhydride : masse volumique : 1 g/mL et masse molaire 102 g/mol ; acide : masse volumique 1 g/mL et masse molaire : 60 g/mol.
  3. La constante d'équilibre K associée à la réaction de synthèse à partir de l'acide vaut K= 4. Déterminer le volume d'acide nécessaire pour obtenir la même quantité d'ester, toujours à partir de 30 mL d'alcool.
  4. Dans quel cas l'état final est-il atteint le plus rapidement ? Justifier.
corrigé
CH3-COOH + CH3-CH2-CH2OH = CH3-COO-(CH2)2-CH3 + H2O

[CH3-CO]2O + CH3-CH2-CH2OH --> CH3-COO-(CH2)2-CH3 + CH3-COOH

Qté de matière (mol) = masse (g) / masse molaire (g/mol)

masse (g) = masse volumique (g/mL) * volume (mL)

n( alcool) = 30*0,8 / 60 = 0,4 mol

n( anhydride) = 20,4*1 / 102 = 0,2 mol ( en défaut)

il se formera 0,2 mol d'ester.

K=[ester][eau] / ([acide][alcool]) = x² / (0,4-x)( n-x)) = 4 avec x = 0,2 mol

0,2²= 4(0,4-0,2)(n-0,2) ; 0,04 = 4*0,2(n-0,2) ; n = 0,25 mol d'acide

masse acide (g) = Qté de matière (mol) * masse molaire (g/mol) = 0,25*60 = 15 g soit 15 mL.

retour -menu