|
étude d'un turboréacteur ; moteur asynchrone triphasé d'après bts FEE 2005 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|
On dissout 96 g de chlorure de sodium (NaCl(s) dans de l'eau à 80°C. La solution obtenue est saturée ; elle a pour volume : 250 mL
Masses molaires : Na : 23 ; Cl : 35,5 g/mol corrigé solubilité du chlorure de sodium à 80°C : masse (g) / volume de la solution (L) = 96/0,25 = 384 g/L. concentration volumique molaire en chlorure de sodium ( mol/L) =solubilité ( g/L) / masse molaire (g/mol) c= 384 / (23+35,5)= 6,6 mol/L. lmasse de chlorure de sodium qui précipite lors du refroidissement : 384-360 =24 g à partir d'un litre de solution soit 24*0,25 = 6 g à partir de 0,25 L de solution. volume minimum d'eau à ajouter : la solubilité à 20 °C est de 360g/L ; dans 250 mL il y a 96 g de chlorure de sodium cette masse de chlorure de sodium est soluble, à 20 °C, dans le volume : 96/360 = 0,267 L il faut donc ajouter : 267 -250 = 17 mL d'eau.
|
||||||||||||||||||||||
|
Un turboréacteur à simple flux comprend un compresseur, une chambre de combustion, une turbine et une tuyère. Le compresseur et la turbine sont montés sur un même arbre. 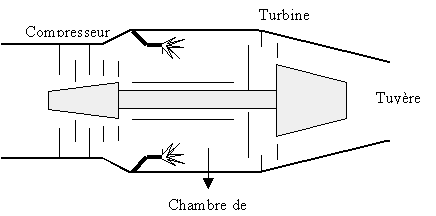 Le compresseur aspire l'air à la pression atmosphérique P0=1 bar à T0=298 K avec un débit massique qm= 60 kg/s et le comprime adiabatiquement jusqu'à la pression P1=4 bars. On assimile l'air à un gaz parfait de constante r= 287 J kg-1 K-1 et de capacité calorifique massique à pression constante cp= 1000 J kg-1 K-1. Les transformations sont considérées réversibles. Relations de Laplace pour un gaz parfait lors d'une transformation adiabatique :PVg=Cte ; PVg-1=Cte ;P1-g Tg=Cte. I - Étude du compresseur :
II - Étude de la chambre de combustion : Le carburant est injecté dans l'air comprimé et brûle sous pression constante dans la chambre de combustion. La combustion s'effectue avec un important excès d'air, on admettra donc qu'il n'y a pas de modification de la nature et du nombre de moles de gaz.
III - Étude de la turbine : Les gaz se détendent adiabatiquement dans la turbine. Soit T3 la température à sa sortie.
g = cp/(cp- r)=1000/(1000-287)=1,4. compression adiabatique : P01-g T0g=P11-g T1g ;T1= (P0 / P1)1/g -1T0 avec 1/g -1= 1/1,4-1 = -0,286 T1= (1/4)-0,286*298 = 443 K. puissance Pc du compresseur : Pc =qmDh avec, pour un gaz parfait : Dh = cpDT= cp(T1-T0)=1000(443-298)=145 kJ kg-1. Pc = 60*145= 8700 kW.
la transformation est isobare : la quantité de chaleur reçue est égale à la variation d'enthalpie Q= 60*1000(1173-443)= 43 800 kJs-1. masse de carburant à injecter par seconde = Q / Qc=43800/43 103
= 1,02 kg.
pour 1 kg d'air et pendant une seconde : W = cpDT= cp(T2-T3) pour qm kg d'air en une seconde : W= qmcp(T2-T3) la détente de l'air dans la turbine fourni un travail au rotor ; le travail est fourni par le fluide au milieu extérieur, donc cela correspond à une valeur négative pour ce travail. puissance Pt recue par la turbine : travail (J) / durée (s) = qmcp(T2-T3) Pc = qm cp(T1-T0) ; Pt=Pc donne : qmcp(T2-T3)=qm cp(T1-T0) soit T2-T3=T1-T0 soit : T3=T2 + T0 - T1= 1173+298-443= 1028 K. pression P3 des gaz à la sortie de la turbine : évolution adiabatique réversible P31-g T3g=P21-g T2g ;P3= (T2 / T3 )g/(1-g )P2 avec g /(1-g)= 1,4/(-0,4)=-3,5 P3= (1173/1028)-3,5*4 = 2,5 bars.
|
|||||||||||||||||||||||
|
Un moteur asynchrone triphasé porte les indications suivantes : 230 V / 400 V ; 50 Hz. Il est alimenté par un réseau 230 V / 400 V ; 50Hz.
corrigé La tension efficace aux bornes des bobines du stator doit être 230 V: donc couplage étoile.
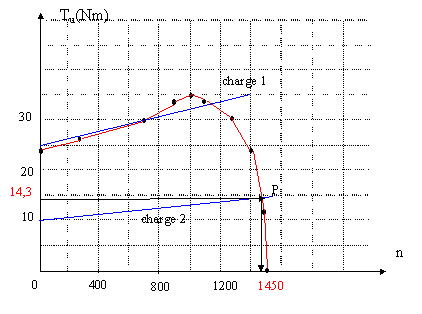
fréquence de synchronisme du moteur : le dernier point du tableau donnd n= ns = 1500 tr/min de plus ns = 3000 / p avec p nombre de paires de pôle et 3000 en tr/min d'où p=2 paires de pôles. Le démarrage en charge du moteur est possible si le couple utile du moteur au démarrage ( n=0) est supérieur au couple résistant opposé par la charge au démarrage. charge 1 : couple résistant ( pour n=0) : 25 Nm charge 2 : couple résistant ( pour n=0) : 10 Nm couple utile pour n=0 : 24 Nm donc le démarrage en charge est possible uniquement pour la charge 2. En régime permanent il y a égalité entre le couple résistant et le couple utile ( point de fonctionnement P du graphe ci-dessus). Tu P= 14,3 Nm et nP= 1450 tr/min. dans ces conditions de fonctionnement le glissement g est donné par : g= (ns-nP)/ns = (1500-1450)/1500 = 0,033 ( 3,3%).
|
|||||||||||||||||||||||
|
|