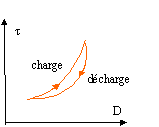|
d'après bts chimie 2001 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
|
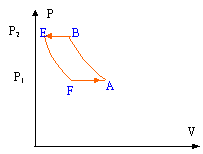
Dans un local fermé, on souhaite maintenir une température T1 = 293 K tandis que l'air extérieur est à la température T2 = 313 K.Pour cela, on considère une machine frigorifique dont le schéma de principe est représenté ci-après : 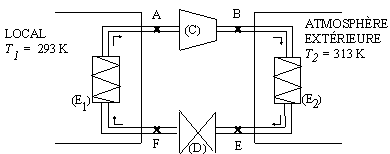
Le fluide qui décrit le cycle est de l'hélium, assimilé à un gaz parfait pour lequel g=5/3 , la capacité thermique massique à pression constante cp = 5260 J.K-1.kg-1 et la masse molaire M = 4,0 g.mol-1. Le fluide traverse successivement : · un compresseur (C) où le fluide subit une compression adiabatique réversible qui l'amène de A (T1, P1) à l'état B (T3, P2). · un échangeur (E2) où la
quantité de chaleur échangée entre le fluide et la source chaude est Q2,
ce qui amène le fluide dans l'état E (T2, P2). · un échangeur (E1) où la quantité de chaleur échangée entre le fluide et la source froide est Q1, ce qui ramène le fluide dans l'état initial A (T1, P1). On donne :P1 = 2,0 105 Pa ; P2= 3,0 105 Pa; R = 8,31 J.K-1.mol-1.
corrigé transformation adiabatique PVg est constant et PV= nRT ; V= nRT/P P [nRT/P ]gest constant soit encore P1-gTg= Cte ou bien P1/g -1 T= Cte avec 1/g -1 = = 3/5-1 = -0,4. A--> B : P1-0,4 T1 = P2-0,4 T3 d'où T3 = (P1/P2)-0,4 T1 =(2/3)-0,4*293 = 344,6 K. E--> F : P2-0,4 T2 = P1-0,4 T4 d'où T4 = (P2/P1)-0,4 T2 =(3/2)-0,4*313 = 266 K.
sur le cycle l'énergie interne ne varie pas : SW + SQ =0 B-->E : Q2 = Cp(T2-T3)= 5260 (313-344,6) = -166216 J/kg ou -166,2 kJ/kg. F-->A : Q1 = Cp(T1-T4)= 5260 (293-266) = 142020 J/kg ou 142 kJ/kg. A--> B et E--> F adiabatique donc Q=0 Wu + Q1 + Q2 =0 donne Wu = -(Q1 + Q2)=166,2-142= 24,2 kJ/kg. efficacité = énergie thermique enlevée à la source froide divisée par le travail investi efficacité de la machine : é=Q1/ Wu =142,2/24,2 = 5,9. Puissance thermique = 2,6 kW ou 2,6 kJ s-1. Puissance du moteur : Pmot = Pth/ éfficacité = 2,6 / 5,9 = 0,44 kW. masse d'hélium ( en une seconde) : 166,2 kJ correspond à 1 kg d'où : 2,6/166,2 = 0,0156 kg/s.
|
|||||||||||||||||||||||||||||||||
|
Un jus de fruit a été élaboré en ajoutant du concentré de fruit à de l'eau sucrée. On étudie d'abord la viscosité de l'eau sucrée qui se comporte comme un fluide newtonien, puis le comportement du jus de fruit obtenu. A. Étude de l'eau sucrée au viscosimètre à chute de bille.
II. Etude rhéologique du jus de fruit.
corrigé 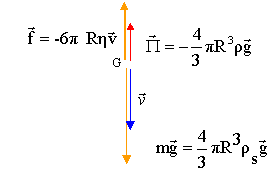
La bille est soumise à son poids, à la poussée d'Archimède P et à la force de frottement fluide. La bille est pseudo-isolée lorsque la vitesse limite est atteinte : la somme des forces est nulle. 4/3pR3rsg = 4/3pR3rg + 6pRhv0. 4/3R2rsg - 4/3R2rg = 6hv0 ; v0= 4/3R2g(rs-r)/ ( 6h)=2/9R2g(rs-r)/ h= d/t 2/9R2g(rs-r)/ h= d/t ; h= 2/9R2g/ d (rs-r) t = K(rs-r) t Si un fluide, à température constante, a une viscosité qui reste constante quelque soit la valeur de la contrainte appliquée, on dit que ce fluide est newtonien . K = 8,94 10-8 Pa.kg-1.m3
; rs
= 7,88 103 kg.m-3 ; r = 1,01 103
kg.m-3. t = 17,2 s.
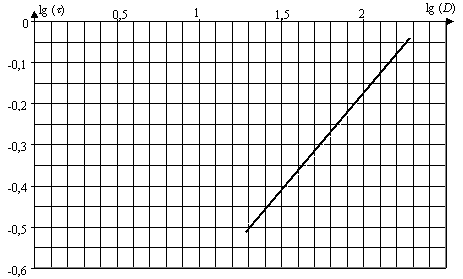
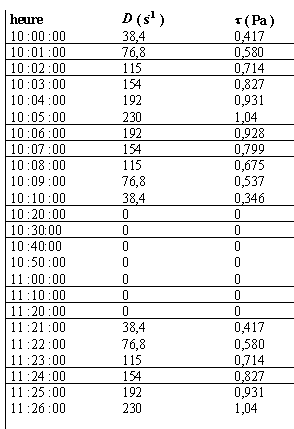
le graphe log(t) en fonction de log(D) est une droite, donc log(t) et log(D) sont proportionnels : log(t) = n log(D) + constante soit encore log(t) = log(Dn) + log k ( k= constante) ; t = kDn où k et n sont des constantes. n : coefficient directeur de le droite ( graphe log(t) en fonction de log(D)) ; n voisin 0,47/1 = 0,47.
La structure a été modifiée durablement lors de la charge et le comportement du produit est affecté ( rhéogramme de décharge différent , liquide globalement moins visqueux Si le temps de repos est supérieur ou égal à une heure on retrouve le comportement rhéologique du produit avant toute charge. On dit alors que le fluide est thixotrope.
|
||||||||||||||||||||||||||||||||||
|
|