Aurélie dec 04

Thermodynamique ; acoustique ; oxydo-réduction

d'après bts Bâtiment 2004

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


thermodynamique ( 8 points)

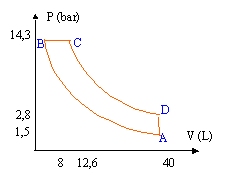
On considère un volume d'air ( gaz supposé parfait) dans un état A : VA= 40 L ; qA= 27°C ; PA= 1,5 105 Pa.

  1. Calculer la quantité de matière correspondante ( nombre de mole)
  2. On effectue les transformations suivantes sur ce gaz :
    a. Une transformation adiabatique réversible de l'état A à l'état B telle que VB= 8 L.
    b. Une transformation isobare de l'état B à l'état C telle que qC= 627 °C
    c. Une transformation adiabatique réversible de l'état C à l'état D.
    d. Une transformation isochore de l'état D à l'état A.
    - Définir les trois types de transformations : isobare, isochore, adiabatique.
    - Déterminer la pression, le volume et la température de chaque point du cycle A-B-C-D.
    - Représenter le cycle dans le diagramme de Clapeyron P= f(V)
    - Calculer la quantité de chaleur totale échangée lors du cycle.
    - En appliquant le premier principe de la thermodynamique, déduire le travail total échangé dans ce cycle.

R= 8,31 J K-1 mol-1 ; Cp= 29,1 J mol-1 K-1 ; Cv = 20,8 J mol-1 K-1.

 

corrigé
loi des gaz parfaits PV= nRT

avec VA= 0,04 m3 ; TA= 27+273 = 300 K ; PA= 1,5 105 Pa. ; R= 8,3 J K-1 mol-1.

n= PV/ (RT)=1,5 105 *0,04/(8,31*300) = 2,41 mol.

adiabatique : pas d'échange thermique entre le sustème et l'extérieur.

isobare : la pression reste constante.

isochore : le volume reste constant.

transformation adiabatique réversible de l'état A à l'état B telle que VB= 0,008 m3.

PAVAg= PBVBg soit PB = PA(VA/VB)g= 1,5 105(40/8)1,4= 1,43 106 Pa.

loi des gaz parfaits PBVB = nRTB soit TB = PBVB /( nR)= 1,43 106*0,008 / (2,41*8,31)= 570 K.

transformation isobare de l'état B à l'état C telle que TC= 627 +273 = 900 K

loi des gaz parfaits PCVC = nRTC soit VC = nRTC / PC = nRTC / PB = 2,41*8,31*900/1,43 106= 1,26 10-2 m3 .

transformation adiabatique réversible de l'état C à l'état D :

PCVCg= PDVDg et transformation isochore de l'état D à l'état A : VA= VD= 0,04 L

soit PD = PC(VC/VD)g= 1,43 106 (12,6/40)1,4= 2,84 105 Pa.

loi des gaz parfaits PDVD = nRTD soit TD = PDVD /( nR)= 2,84 105*0,04 / (2,41*8,31)= 567 K.

Quantité de chaleur totale échangée lors du cycle :

pas d'échange de chaleur pour les transformations adiabatiques

isobare : Q= n Cp DT = n Cp (TC -TB)= 2,41 * 29,1(900-570)= 2,31 104 J.

isochore : Q= n Cv DT = n Cv (TA -TD)= 2,41 * 20,8(300-567)= -1,34 104 J.

total : Qcycle= 2,31 104 -1,34 104 = 9,7 103 J.

la variation d'énergie interne du gaz est nulle sur le cycle, d'où Wcycle= - Qcycle= -9,7 103 J.


acoustique (6 points)

On se propose d'étudier du point de vue acoustique, une paroi composée ( mur + fenètre) d'une chambre d'appartement donnant sur une rue. La paroi est représentée ci-dessous :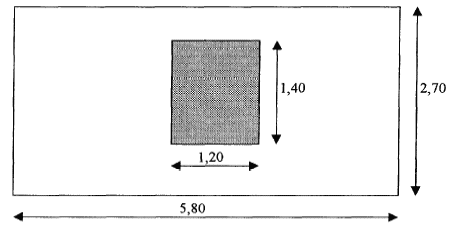

L'analyse par bande d'octave du bruit de la rue donne les résultats suivants :
bandes d'octaves en Hz
125
250
500
1000
2000
niveau d'intensité L (dB)
71
70
66
65
57
intensité sonore Wm-2


10-5
4 10-6


5 10-7

  1. Démontrer que l'intensité sonore pour 125 Hz s'écrit : I125 = I0 10 L125/10. Compléter le tableau.
  2. Démontrer que le niveau d'intensité global LS s'écrit : LS= log (SIi/I0). Calculer sa valeur.
  3. Sachant que la masse volumique du mur est rm= 2100 kg m-3 et que son épaisseur est em= 20 cm, déterminer sa masse surfacique sm. Calculer l'indice d'affaiblissement du mur noté Rm. En déduire le facteur de transmission tm du mur.
  4. Sachant que la masse surfacique du verre est sf =7 kg m-2, déterminer l'indiceRf d'affaiblissement de la fenètre. En déduire le facteur de transmission tf de la fenètre.
  5. Calculer le facteur de transmission global tg de la paroi composée. Déterminer l'indice d'affaiblissement global Rg. Calculer le niveau sonore d'intensité dans la chambre si l'on ne tient pas compte des phénomènes de réverbération.

L= 10 log (I/I0) avec I0 = 10-12 Wm-2.

Loi de masse : R= 17 log s +4 si s <150 kg m-2 ; R= 40 log s -46 si s >150 kg m-2 ; R= 10 log (1/t).

t g= St iSi / S Si.

corrigé
L= 10 log (I/I0) s'écrit : L/10 = log (I/I0) puis 10L/10 = I/I0 ; I= I0 10L/10 = 10-12 10L/10

bandes d'octaves en Hz
125
250
500
1000
2000
niveau d'intensité L (dB)
71
70
66
65
57
intensité sonore Wm-2
10-12 107,1

= 10-4,9

=1,26 10-5
10-5
4 10-6
10-12 106,5

=10-5,5

=3,16 10-6
5 10-7
I / I0
1,26 107
107
4 106
3,16 106
5 105
Les intensité sonores s'ajoutent : Itotal = I125 + I250+I500+I1000+I2000 = SIi avec Ii= I0 10Li/10.

Itotal =I0 10-L125/10 + I0 10-L250/10.....+ I0 10-L2000/10 = I0S10Li/10.

Itotal /I0 = S10Li/10 ; soit LS=10 log(Itotal /I0 )= 10 log (SIi/I0)

SIi/I0 = 1,26 107 +107 + 4 106 + 3,16 106 + 5 105 = 3,026 107.

LS= 10 log 3,026 107= 74,8.

masse surfacique du mur = masse d'un volume égal à m3 *épaisseur (m) = sm= 2100 * 0,2 = 420 kg m-2

indice d'affaiblissement du mur noté Rm=40 log s -46= 40 log 420 -46 = 58,9.

facteur de transmission tm du mur : R= 10 log (1/tm) s'écrit : 1/tm = 10R/10 = 7,76 105 soit tm = 1,29 10-6.

indice d'affaiblissement du verre noté Rf =17 log sf +4 = 17 log7 +4 = 18,4.

facteur de transmission tf de la fenètre : Rf= 10 log (1/tf ) s'écrit : 1/tf = 10R/10 = 69,1 soit tf = 1,45 10-2.

facteur de transmission global tg de la paroi composée t g= St iSi / S Si.

surface de la fenêtre : 1,2*1,4 = 1,68 m² ; surface du mur : 5,8*2,7-1,68 = 13,98 m² ; surface totale = 15,66 m²

(1,29 10-6 *13,98 + 1,45 10-2 *1,68)/ 15,66 = 1,56 10-3.

indice d'affaiblissement global Rg = 10 log (1/tg ) = 10 log (1/1,56 10-3) = 28,1 dB

niveau sonore d'intensité dans la chambre 74,8-28,1 = 46,6 dB.

oxydo-réduction (6 points)

Le chassis d'une fenêtre d'appartement est en aluminium. Il peut se détériorer au contact de l'air humide ( O2 + H2O). Les couples d'oxydoréduction mis en jeu sont : O2 / H2O E°=0,4 V ; Al3+/Al E°= -1,66 V

  1. Quel est l'oxydant le plus fort ? Justifier.
  2. Ecrire la demi équation électronique concernant le couple Al3+/Al.
    - Equilibrer la demi-équation électronique concernant le couple O2/H2O et indiquer le sens de lé réaction.
    O2 + H2O + e- = HO-.
    Est ce une oxydation ou une réduction ? Justifier.
  3. Justifier que l'équation bilan de la réaction d'oxydoréduction s'écrit : 2Al + 1,5 O2 + 3 H2O = 2Al3++6 HO-
  4. Sur l'ensemble du châssis, il s'est formé 16 g d'hydroxyde d'aluminium Al(OH)3 ; calculer la masse d'aluminium détérioré. H: 1 ; O: 16 ; Al : 27 g/mol
corrigé
Le réducteur le plus fort est la forme réduite du couple ayant le plus petit potentiel soit Al. En conséquence l'oxydant le plus fort est la forme oxydée de l'autre couple soit O2.

2 fois {Al = Al3++ 3e-} oxydation du réducteur Al

3 fois { ½O2 + H2O + 2e- =2 HO-} réduction ( gain d'électrons) de l'oxydant O2

évolue vers la droite, sens direct.

2Al + 1,5 O2 + 3 H2O = 2Al3++6 HO-

ou bien 2Al + 1,5 O2 + 3 H2O =2 Al(OH)3.

masse molaire Al(OH)3 : M=27 + 3*(1+16) = 78 g/mol

Qté de matière hydroxyde d'aluminium : masse (g) / masse molaire (g/mol) = 16 /78 = 0,205 mol

D'après les coefficients de l'équation bilan, 0,205 mol d'aluminium est détérioré.

masse aluminium (g) = Qté de matière (mol) * masse molaire Al = 0,205*27 =5,54 g.

retour -menu