|
d'après bac Amérique du Nord 2005. En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|||
|
|||
|
|
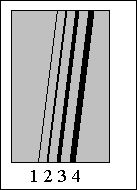
Les instruments du quatuor (deux violons, un alto, un violoncelle) sont de la famille des cordes frottées. Lorsque l'on frotte l'archet sur une corde, on produit une vibration très particulière, différente de celle produite par un marteau sur une corde de piano. La corde est entraînée par l'archet ; quand l'adhérence cesse la corde glisse en sens opposé, puis elle est à nouveau entraînée par l'archet, etc… Ce mouvement très rapide donne un timbre particulier aux instruments à cordes frottées. La vibration est entretenue tant que l'instrumentiste fait adhérer l'archet à la corde. L'obtention de sons plus ou moins graves s'obtient en faisant varier plusieurs paramètres de la corde vibrante : - l'épaisseur de la corde e : les cordes épaisses produisent un son grave, les cordes fines un son aigu; - la longueur de la corde L ; - la tension de la corde F : ce réglage se fait par l'intermédiaire de chevilles. Plus la corde est tendue, plus le son est aigu.
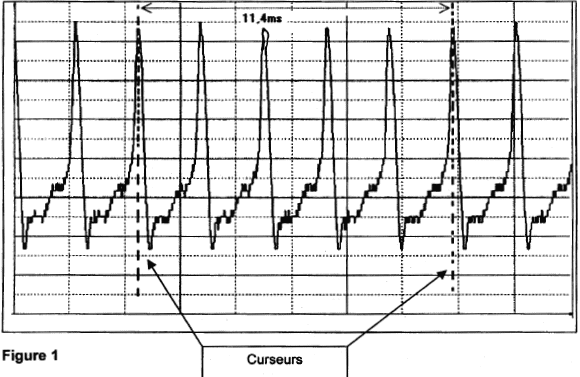
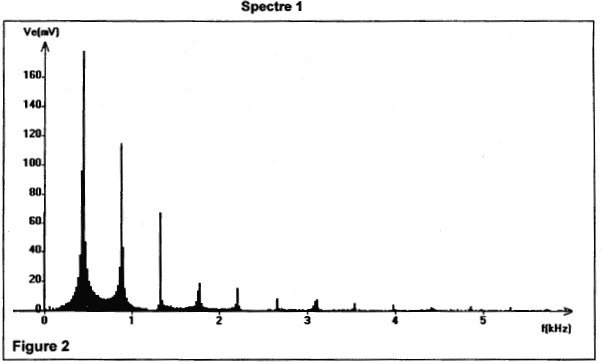
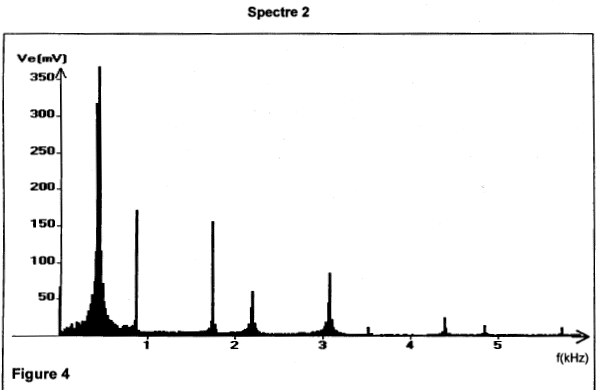
La corde 1 correspond donc au mi4 , la corde 2 au la3 , la corde 3 au ré3 et la corde 4 au sol2 . v = (F/m)½ = ( 245 / 2,9.10-3)½ = 290 m.s-1. v = l fk ; de plus l=2L/k ; fk = v / l = k v / (2L) Pour le mode fondamental, k = 1. f = v / 2L = 290/(2*0,33)= 440 Hz. ( corde question 1 b) La célérité est proportionnelle à la racine carrée de la tension de la corde : plus la corde est tendue, plus la célérité v est grande et en conséquence plus la fréquence f du son augmente ( son de plus en plus aigu). En diminuant la longueur de la corde (appuyer sur la corde avec un doigt ), on augmente la célérité v et en conséquence la fréquence : le son est donc plus aigu. Lecture figure 1 : 5 périodes valent 11,4 ms. T = 11,4 / 5 = 2,28 ms = 2,28 10-3 s. f1 = 1 / T = 1 / 2,28.10-3 = 439 Hz. La fréquence f1 du mode fondamental correspond à la fréquence du son. La fréquence du fondamental correspond au premier pic. f1 = 0,42 kHz = 420 Hz
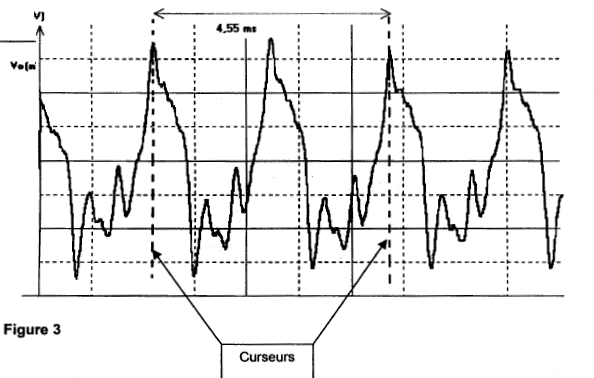
Les fréquences des harmoniques sont des multiples de la fréquence du fondamental. f2 = 2 f1 = 840 Hz ; f3 = 3 f1 = 1260 Hz ; f4 = 4 f1 = 1680 Hz. La hauteur d'un son est caractérisée par sa fréquence du fondamental. Calcul de la période T2 du 2ème son : 2 T2 = 4,55 ms ; T2 = 2,28 ms= 2,28 10-3 s ; f2 = 1 / T2 = 439 Hz f1 est voisine de f2 . Ces deux sons ont la même hauteur. Son timbre ( il dépend de la composition des harmoniques) permet de distinguer deux notes de même hauteur jouée par deux instruments différents Les sons émis par les deux instruments n'ont pas le même timbre car les spectres des 2 sons sont différents, la 2ème harmonique est absente du spectre du 2ème son.
|
||
|
|