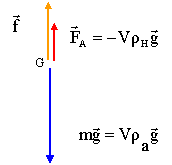|
d'après bac Reunion 2005 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
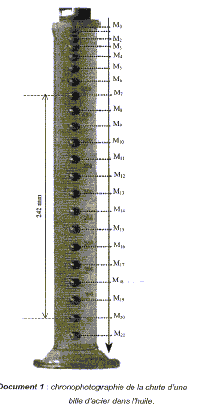
Données : volume de la bille en acier V= 0,52 cm3 ; masse volumique de l'acier ra= 7850 kgm-3 ; masse volumique de l'huile rH= 920 kg m-3 ; g= 9,8 m/s². On réalise la chronophotographie d'une bille sphérique en acier dans l'huile. Pour ce faire, on filme la bille dans une éprouvette remplie d'huile, avec un camescope numérique au rythme de 50 images par seconde. Gràce à un traitement adéquat des images on obtient le document ci-dessous. On repère ensuite la position sur chaque image, du centre d'inertie de la bille : M0 correspond à sa position initiale, celle-ci étant lâchée, à un instant t0 pris comme origine des dates, sans vitesse initiale.
B. étude cinématique : Le point M0 étant pris comme origine des espaces et des temps, on repère les différentes hauteurs réelles de la chute de la bille dans l'huile, notées y aux dates t correspondantes. On calcule alors les vitesses correspondantes.
C. étude dynamique :
D. équation différentielle du mouvement de la bille : Soit f l'intensité de la force de frottement à laquelle est soumise la bille en mouvement dans l'huile.
E. Recherche de modèles pour la force de frottement : On se propose de déterminer expérimentalement si l'intensité de la force de frottement f à laquelle est soumise la bille en mouvement dans l'huile est de la forme f=k1v ou f= k2v². k1 et k2 étant des constantes et v étant la vitesse de la bille. On utilise un tableur pour représenter la vitesse de la bille en fonction du temps. On obtient le graphe suivant où les points expérimentaux sont représentés sous forme de losange. On détermine ainsi la vitesse limite de chute de la bille vl= 0,95 m/s. 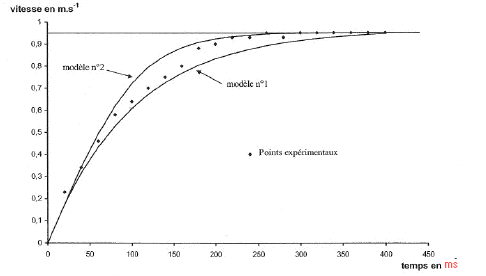
corrigé La trajectoire est une droite verticale et la vitesse est constante entre M13 et M21 : le mouvement de la bille est donc un mouvement rectiligne uniforme, ce qui illustre le principe d'inertie ou 1ère loi de newton ( dans un référentiel galiléen, si un solide est pseudo-isolé, somme vectorielle des forces nulle, alors le centre de gravité G du solide est soit au repos, soit animé d'un mouvement rectiligne uniforme) On filme sur un rythme de 50 images par seconde. La durée
séparant deux images consécutives est donc : 1/50 = 0,02 s = 20 ms.
Le vecteur l'accélération traduit la variation du vecteur vitesse ; les vecteurs vitesses sont tous colinéaires et de même sens, celui du mouvement , en conséquence on peut écrire une relation entres les valeurs : a18 = Dv/Dt = (v19-v17) / (t19-t17) =(0,95-0,95) (380-340)10-3)= 0 m/s². seconde loi de Newton : dans un référentiel galiléen la somme vectorielle des forces extérieures appliquées à un solide de masse m, est égale au produit de la masse du solide par le vecteur accélération de son centre d'inertie G. Si l'accélération est nulle, alors la somme vectorielle des forces est nulle. Et d'après le
principe d'inertie, le mouvement du centre d'inertie du solide est
rectiligne uniforme ( conclusion compatible avec le résultat ci-dessus)
masse de la bille (kg) = volume de la bille (m3) * masse volumique acier (kg m-3) V= 5,2 10-5 m3 ; m= 5,2 10-7*7850 = 4,1 10-3 kg = 4,1 g. poussée d'Archimède = poids du volume de fluide déplacé = VrH g FA=
5,2 10-7*920*9,8 = 4,7 10-3 N.
projection de la somme des forces sur un axe vertical descendant : mg-FA-f= ma = m dv/dt diviser chaque terme par m : g-FA/m-f/m =dv/dt dv/dt + f/m = g-FA/m , on identifie A à : g-FA/m A= 9,8- 4,7 10-3 / 4,1 10-3 = 8,7 m/s². cette constante
est homogène à une accélération.
on identifie B1 à k1/m Quand la vitesse limite est atteinte dvl/dt = 0 soit B1 vl=A ou B1 =A / vl; de plus B1 = k1/m d'où : k1/m=A / vl ; k1=mA/ vl ; A est en m s-2 ; m en kg et vl en m s-1 donc k1 en kg s-1 k1 = 4,1 10-3 *8,7/0,95 = 3,7 10-2 kg s-1. hypothèse n°2 : dv/dt + k2/m v2 = A on identifie B2 à k2/m Quand la vitesse limite est atteinte dvl/dt = 0 soit B2 vl2=A k2/m vl2=A soit k2 = mA/vl2; A est en m s-2 ; m en kg et vl en m s-1 donc k1 en kg m-1 k2 =4,1 10-3 *8,7/0,95 2= 3,9 10-2 kg m-1. sur le graphe regarder dans quel cas les courbes théorique et expérimentale coïncident : si 0<v<0,8 m/s, le modèle n°1 convient si 0,8< v<1m/s, le modèle n°2 convient.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Une bouteille d'ammoniaque du commerce comporte l'indication 22 ° Bé, ce qui correspond à une concentration molaire C0 = 10,9 mol.L-1.Cette solution sera nommée S0. Dans une solution aqueuse d'ammoniac, l'équilibre entre l'ammoniac NH3 et les ions ammonium NH4+ s'écrit : NH3 (aq) + H2O (I) = HO- (aq) + NH4+ (aq). Données (valeurs à 25 °C): Quotient de la réaction de l'ammoniac avec l'eau à l'équilibre : Qr,éq= 1,58.10-5 Produit ionique de l'eau : Ke = 1,00.10-14. 1ère partie : Détermination du quotient de réaction par pHmétrie : La " basicité " de la solution S0 étant trop élevée pour être mesurée directement au pHmètre, on prépare 50,0 mL d'une solution diluée S1 de concentration C1 = C0 /10. Le pH mesuré de S1 est 11,62.
2ème partie : Détermination du taux d'avancement de la réaction de l'ammoniac sur l'eau par conductimétrie : Valeurs des conductivités molaires ioniques à 25 °C : l°( HO-) = 19.9.10-3 S.m2.mol-1 ; l °( NH4+) = 7.34.10-3 S.m2.mol-1. L'expression de la conductivité d'une solution s = S l i [ Xi] n'est valide qu'en solution très diluée. A partir de la solution S1 d'ammoniac, on prépare une solution fille, nommée S2 de concentration C2 = C1/100 = C0/1000. A) Hypothèse: On fait l'hypothèse que les quantités de matière des espèces en solution n'ont pas changé lors de la dilution.
B) Conductimétrie: Pour confirmer ou infirmer l'hypothèse précédente, on mesure la conductivité s de la solution S2: s = 0,114 mS.cm-1.
corrigé Le facteur de dilution est 10 ; volume fiole jaugée (mL) / volume pipette jaugée (mL)=10 soit volume pipette jaugée = volume fiole jaugée / 10 = 50 /10 = 5,0 mL. port de gants, lunette et blouse pour prélever 5 mL de solution mère à la pipette jaugée verser dans une fiole jaugée de 50 mL contenant un peu d'eau distillée compléter à l'aide d'eau distillée jusqu'au trait de jauge. [ H3O+] = 10-pH= 10-11,62 = 2,4 10-12 mol/L [HO-](s1)=10-14/ [ H3O+] = 10-14/ 2,4 10-12 = 4,2.10-3 mol.L-1.
la réaction de l'ammoniac avec l'eau est très limitée. quotient de réaction Qr,1 à l'état final : Qr,1 =[HO-]f[NH4+ ]f/[NH3]f= xf2 / 1,09-xf = (4,2 10-3)2/(1,09-4,2 10-3 )=1,6 10-5. l'écart avec Qr,éq= 1,58.10-5 est inférieur à 3%. Donc dans l'état final le système est à l'équilibre. Le facteur de dilution ( à partir de S1) est de 100. [HO-](hyp) = 10-2[HO-](s1) ; [NH4+](hyp) =10-2 [NH4+] (s1) ; [NH3] (hyp) =10-2 [NH3] (s1). Qr,hyp = [HO-]hyp[NH4+ ]hyp/[NH3]hyp =10-2 [HO-](s1) 10-2 [NH4+] (s1) /(10-2 [NH3] (s1))=Qr,1/100. Qr,hyp = 1,6 10-5 / 100 = 1,6 10-7, valeur inférieure à la constante d'équilibre. l'hypothèse n'est pas vérifiée. Qr,hyp est inférieure, dans cette hypothèse, à la constante d'équilibre : le critère d'évolution spontané prévoit une évolution du système dans le sens direct. Donc une modification des concentrations lors de la dilution. s = 0,114 mS.cm-1. valeur de s dans le système international : 1 mS= 10-3 S ; 1 cm= 10-2 m ; 1 cm-1 = 100 m. s = 0,114 10-3 *100 = 1,14 10-2 Sm-1. conductivité s de la solution S2 : s =l °( NH4+)[NH4+] (s2) + l°( HO-) [HO-](s2)= (l °( NH4+) +l°( HO-))[HO-](s2) [HO-](s2)= s /(l °( NH4+) +l°( HO-))= 1,14 10-2/((19,9+7,34)10-3)= 4,2 10-1 mol m-3 = 4,2 10-4 mol /L xf= 4,2 10-4 mol ; xmax = 1,09 10-2 ( du fait de la dilution par 100) ; t2= 4,2 10-4 / 1,09 10-2 = 4,2 10-2. La dilution de la solution mère agit sur le taux d'avancement de la réaction de l'ammoniac sur l'eau : ce dernier augmente, il a presque été multiplié par 10. L'hypothèse émise dans la partie 1 n'est pas confirmée. .
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Données : Numéro atomique de l'élément iode : Z(l) = 53. La thyroïde est une glande, située dans la région cervicale antérieure, appliquée contre le larynx et la partie supérieure de la trachée. La fonction principale de cette glande est la sécrétion des hormones thyroïdiennes à partir de l'Iode alimentaire qui se fixe temporairement sur cette glande. De petite taille, pesant 15 à 25 g chez l'adulte et mesurant environ 4 cm en largeur et 3 cm en hauteur, elle n'est normalement pas, ou à peine, palpable. Mais elle peut s'hypertrophier, soit de manière plus ou moins diffuse et homogène, soit de manière localisée avec la formation de nodule(s). Ces nodules peuvent principalement être de deux sortes : hypofixant ou hyperfixant. Ils sont dits hypofixants s'ils fixent peu d'iode par rapport au reste de la thyroïde. Inversement, ils sont dits hyperfixants s'ils fixent plus d'iode que le reste de la thyroïde. Ce sont ces nodules qu'il faut déceler pour traiter le patient si nécessaire. Ceci est réalisé à l'aide de traceurs radioactifs, les isotopes 123I et 131I, de constantes radioactives respectives l123 = 1,459 10-5 s-1 et l131 = 1,001 10-6 s-1. Ces isotopes sont en effet des émetteurs de rayons gamma pouvant être détectés par un appareil de mesure appelé "détecteur à scintillations". La condition pour que l'appareil de mesure utilisé ici compte les rayons gamma, est que ceux-ci aient une énergie supérieure à 20 eV. Il en résulte alors une image reconstituée de l'organe étudié, sur laquelle les zones foncées représentent les zones de l'organe fortement émettrices en rayons gamma. La scintigraphie est donc une sorte de photographie. Lorsque l'analyse est pressée, on préfère utiliser l'isotope 123I qui nécessite un temps de pose de l'ordre du quart d'heure. On injecte alors, au patient, une dose de 123I, d'activité A = 7,0 MBq, contenu dans une solution d'iodure de sodium NaI où l'iode est le traceur radioactif. On laisse alors l'iode se fixer, soit environ 4 heures, temps au bout duquel on réalise la scintigraphie. A) Choix de l'isotope 123I :
B) Administration de l'iode à un ensemble de patients. L'hôpital commande un flacon d'une solution de NaI avec de l'iode 123I, pour l'utiliser sur plusieurs patients. Pour des raisons pratiques, les injections sont effectuées toutes les 30 minutes. La première injection a lieu le matin à 9 h. Juste avant cette injection, l'activité du flacon de l'hôpital est de 28,5 MBq. A chaque injection, on prélève une dose d'activité égale à 7 MBq.
C) Précaution et analyse des images obtenues.
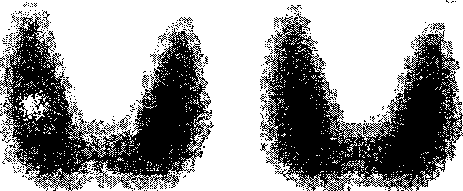
corrigé 21H + 12252Te--> 12353I +AZX conservation de la charge : 1+52=53 +Z soit Z=0 conservation du nombre de nucléons : 2+122=123+A soit A= 1 la particule X est donc un neutron. temps de demi-vie des deux isotopes : lt½ =ln2 123I : t½ =ln2 /l123 =ln2/ 1,459 10-5 = 4,75 104 s 131I : t½ =ln2 /l131 =ln2/ 1,001 10-6 = 6,92 105 s avantage d'utiliser l'isotope 123I par rapport au 131I : la demi-vie ou période de l'isotope 123I est plus
petite que la demi-vie de l'isotope 131I : 123I
disparaît plus rapidement de l'organisme du patient.
valeur de e-lDt, si D t = 30 min = 30*60 = 1800 s e-lDt = exp(-1,459 10-5*1800)=0,974. activité du flacon à 9h30 : A= A0 e-lDt =21,5 *0,974 = 20,9 MBq. immédiatement après la seconde injection, l'activité du flacon est : 20,9-7 = 13,9 Bq 30 min plus tard, l'activité du flacon est : 13,9*0,974 =13,6 Bq. immédiatement après la troisième injection, l'activité du flacon est : 13,6-7 = 6,6 Bq. On peut traiter trois patients.
A=lN soit N= A/l=7 106 / 1,459 10-5 =4,8 1011 noyaux. 6 semaines = 6*7*24*3600 secondes soit 3,63 106s. valeur de e-lDt, si D t = 3,63 106 s e-lDt = exp(-1,459 10-5*3,63 106)= 10-23. activité résiduelle due à la première injection :7 106* 10-23 = 7 10-17 Bq l'activité résiduelle due à la première injection étant nulle, celle-ci n'influence pas la seconde analyse. Ils sont dits hypofixants s'ils fixent peu d'iode par rapport au reste de la thyroïde, ce qui correspond à l'observation d' une tache plus claire sur l'image proposée.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|