Aurélie novembre 04

Projectile

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


 Un joueur de tennis est situé en A à la distance D= 9 m du filet et tente de lober son adversaire situé en B à une distance d= 2 m du filet. Le joueur frappe la balle à une hauteur h=0,5 m du sol avec un angle de tir a = 60° et une vitesse v0= 43,2 km/h. On assimile la balle à un point matériel de masse m= 60 g. g= 10 m/s² ; les frottements sont négligés.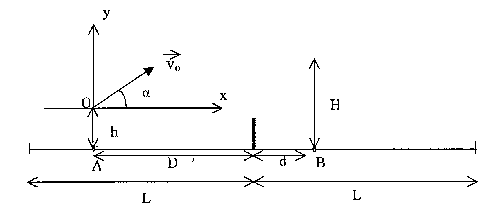

  1. Quelle est l'énergie cinétique de la balle au moment où elle quitte la raquette ?
  2. Quelles sont les affirmations suivantes qui sont vraies ?
    -a La balle de tennis a un mouvement de chute libre.
    -b Le vecteur accélération du centre d'inertie de la balle est égal au poids de la balle.
    -c Le mouvement de la projection du centre d'inertie de la balle suivant l'axe horizontal Ox est uniformément varié.
    a: seule ; b : seule ; c :seule ; a et b ; a et c ; b et c ; toutes; aucune.
  3. Quelle est l'altitude maximale de la balle par rapport au sol ?
  4. Combien de temps met la balle pour atteindre la hauteur maximale ?
  5. Quelle est l'altitude de la balle par rapport au sol lorsqu'elle passe juste au dessus de B ?
  6. A quelle distance du point A se situe le premier point d'impact au sol ?
  7. Sachant que la longueur totale du terrain et 2L= 24 m, quelle est la vitesse maximale que le joueur A peut donner à la balle pour quelle retombe à coup sur dans le terrain, l'angle restant le même ?

corrigé
énergie cinétique de la balle au moment où elle quitte la raquette : ½mv²

avec m= 0,06 kg et v0 = 43,2/3,6 = 12 m/s ; Ec= 0,5*0,06*12² = 4,32 J.

a) La balle de tennis a un mouvement de chute libre ( elle n'est soumise qu' à son poids).
b) Le vecteur accélération du centre d'inertie de la balle est égal à g.
c) Le mouvement de la projection du centre d'inertie de la balle suivant l'axe horizontal Ox est uniforme.
a: seule.

accélération : ( 0 ; -g) soit (0 ; -10)

vitesse initiale (v0cos a ; v0 sin a ) soit (6 ; 10,39)

position initiale : origine du repère

vitesse, primitive de l'accélération : v0cos a ; -gt +v0 sin a ) soit (6 ; -10 t+10,39)

position, primitive de la vitesse : x= v0cos a t = 6 t ; y = -½gt² + v0 sin a t = -5t²+10,39 t

trajectoire ( éliminer le temps dans les deux relations précédentes): t= x/( v0cos a) puis repport dans y

y= -½gx²/(v0cosa)² + x tan a = -0,139 x² + 1,732 x.

au sommet S de la trajectoire la vitesse est horizontale : -gt +v0 sin a=0 ; t = v0 sin a/g

repport dans y(t) : yS= -½g v²0 sin² a/g² + v²0 sin² a/g = ½v²0 sin² a/g .

yS=0,5*12² sin²60 / 10 = 5,4 m

ajouter 0,5 m soit 5,9 m au dessus du sol.

xS= v0cos a v0 sin a/g= v²0 sin a cos a/g .

altitude de la balle par rapport au sol lorsqu'elle passe juste au dessus de B :

B est situé à 11 m de A : y = -0,139*11²+1,732 *11 =2,25 m

soit par rapport au sol 2,25 + 0,5 = 2,75 m.

premier point d'impact au sol y = -0,5 m

résoudre : -0,5 = -0,139 x² + 1,732 x.

x= 12,75 m.

vitesse maximale que le joueur A peut donner à la balle pour quelle retombe à coup sur dans le terrain :

x = 9+12 = 21 m ; y= -0,5 m

y= -½gx²/(v0cosa)² + x tan a = -20x² /v²0+ 1,732 x

v²0= 20 /(1,732x-y) = 20 x² /(1,732*21-(-0,5))= 239,2 soit v0 = 15,47 m/s.


retour -menu