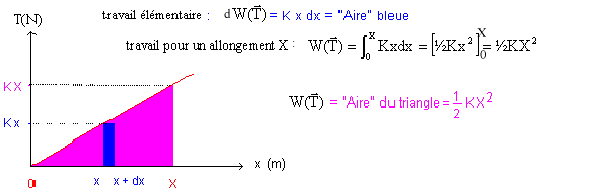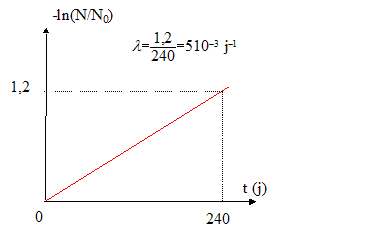|
d'après bac Polynésie sept 2005. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
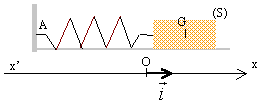
Notre objectif est d'étudier le mouvement d'une masse m attachée à un support immobile par un ressort horizontal de constante de raideur k. I - L'oscillateur harmonique : Une masse est libre de se déplacer sans frottement sur un rail horizontal. Après avoir écarté la masse de sa position d'équilibre, on la libère sans vitesse initiale.
II - Etude énergétique
III - Application à la molécule de chlorure d'hydrogène : Notre objectif est d'étudier le mouvement de vibration d'une molécule de chlorure d'hydrogène (HCI). Cette molécule peut-être modélisée par une masse m correspondant à l'atome d'hydrogène, un support immobile correspondant à l'atome de chlore, les deux parties étant reliées par un ressort de constante de raideur k qui représente la liaison entre les deux atomes.
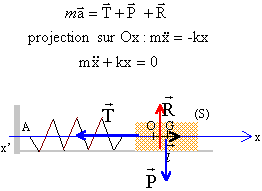
corrigé forces agissant sur la masse m : action du support verticale vers le haut, valeur R , poids , vertical vers le bas valeur mg, tension du ressort, horizontale, valeur kx. La seconde loi de Newton s'écrit :
équation différentielle : md²x/dt² +k x =0 soit d²x/dt² + k/m x=0 on pose : w0² =k/m x(t) = A.sin(w0 t+j ) dériver par rapport au temps : dx/dt = Aw0cos(w0 t+j ) dériver à nouveau par rapport au temps : d²x/dt² = -Aw0²sin(w0 t+j ) = - Ak/msin(w0 t+j ) repport dans l'équation différentielle : - Ak/m sin(w0 t+j ) + Ak/m sin(w0 t+j ) =0 est vérifiée quel que soit t donc x(t) = A.sin(w0 t+j ) est solution de cette équation différentielle. Déterminer les constantes A et j qui correspondent à ces conditions initiales : vitesse initiale[dx/dt]t=0 =0 soit = Aw0cos(j ) = 0 donc j = p/2 ou bien j = -p/2. x(t=0) =0,02 m soit 0,02 = A.sin(j ) A amplitude positive égale à 0,02 m, donc j = p/2 rad. période propre T0 des oscillations de l'oscillateur en fonction de k et m : T0 = 2p/w0 = 2p[m/k]½.
expression de l'énergie potentielle élastique du système {masse - ressort} en fonction de l'allongement x : ½kx². expression de l'énergie cinétique de la masse m et de l'énergie totale du système : ½mv² Une masse est libre de se déplacer sans frottement sur un rail horizontal : donc l'énergie mécanique du système est constante. à t=0 l'énergie cinétique est nulle ; l'énergie potentielle élastique vaut : ½kx²0 énergie mécanique du système : ½kx²0 période propre T0 pour la molécule de chlorure d'hydrogène : masse (kg) m = 10-3 / NA = 1/ 6,02 x 1023 = 1,66 10-27 kg et k =510 N.m-1. T0 = 2p[m/k]½ = 6,28[1,66 10-27/510]½=1,13 10-14 s. fréquence f0= 1/T0 =8,82 1013 Hz. On observe un phénomène de résonance si la fréquence n de l'onde est égale à la fréquence propre de l'oscillateur élastique. longueur d'onde dans le vide correspondant à cette fréquence : l0= c/f0= 3 108 / 8,82 1013 = 3,4 10-6 m. domaine de radiation : UV On remplace l'hydrogène par le deutérium noté H de masse double par rapport à celle de l'hydrogène : f0= 1/(2p)[k/m]½ ; si la masse double, la fréquence propre est divisée par racine carrée de deux 8,82 1013 / 1,414 = 6,23 1013 Hz.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
" Le vin est une boisson provenant exclusivement de la fermentation du raisin frais ou du jus de raisin frais ".Telle est la définition légale du vin mais derrière le terme " fermentation " se cachent des transformations que les chimistes ont mis des années à découvrir. Dans les années 1960, on commença à s'intéresser à une autre fermentation qui se produit généralement après la fermentation alcoolique et à laquelle on n'attachait pas trop d'importance jusqu'alors car on pensait qu'il s'agissait d'un achèvement de la fermentation alcoolique. Il s'agit de la fermentation malolactique qui consiste en une transformation totale de l'acide malique présent dans le jus de raisin en acide lactique sous l'action de bactéries. Cette fermentation, longtemps ignorée, a une influence reconnue sur la qualité gustative de certains vins à condition de la conduire convenablement. Les techniques actuelles de suivi de ces fermentations se font par dosage enzymatique ; elles consistent essentiellement à doser l'alcool contenu dans le vin. Principe du dosage : Étape 2: L'éthanol est oxydé par la nicotinamide-adénine-dinucléotide (NAD+) dans une réaction catalysée par une enzyme spécifique. La réaction produit de la nicotinamide-adénine-dinucléotide réduite (NADH) en quantité de matière égale à celle de l'éthanol dosé selon l'équation : CH3CH2OH + NAD+ = CH3CHO + NADH + H+ (1). Étape 3 : On mesure l'absorbance de la NADH par spectrophotométrie à la longueur d'onde de 340 nm lors du dosage. A - Détermination du degré alcoolique d'un vin : " On appelle degré alcoolique d'une boisson alcoolisée, le volume (exprimé en mL) d'éthanol contenu dans 100 mL de cette boisson, les volumes étant mesurés à 20°C. " On l'exprime en % vol. I - Questions préliminaires
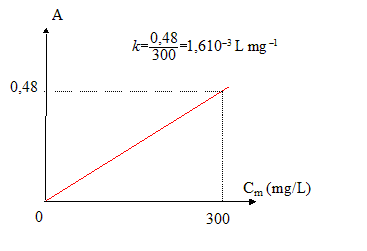
Il - Étalonnage du spectrophotomètre On réalise une gamme de quatre solutions étalons; chaque solution étalon contient : NAD+ en excès, le catalyseur, une solution de concentration massique connue en éthanol. On mesure l'absorbance de chaque solution étalon et on obtient les résultats suivants :
III - Préparation et dosage de l'éthanol contenu dans le vin On distille 20 mL de vin ; le distillat est ensuite ajusté à 200 mL avec de l'eau distillée pour obtenir une solution appelée D. On prépare l'échantillon à doser par spectrophotométrie en introduisant : 1 mL de solution D, le catalyseur, NAD+ en excès, dans une fiole jaugée de 50 mL que l'on complète avec de l'eau distillée. L'absorbance mesurée pour cet échantillon vaut: Ae = 0,30.
Donnée: - Masse volumique de l'éthanol supposée constante dans le domaine de concentration considéré: 0,80 kg.L-1. DEUXIEME PARTIE: cinétique de la fermentation malolactique L'équation de la fermentation malolactique est : COOH-CH2-CHOH-COOH (Acide malique ) = CH3-CHOH-COOH ( Acide lactique)+ CO2 Le dosage enzymatique de l'acide malique restant dans le vin a donné les résultats suivants pour une température de fermentation maintenue à 20°C
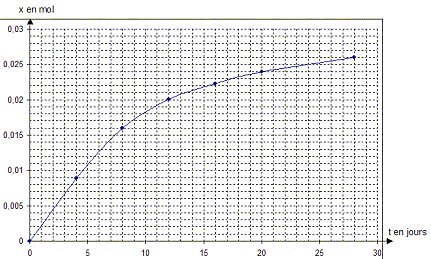
NAD+ + H+ + 2e- = NADH réduction On observe un transfert d'électrons entre la forme réduite CH3CH2OH du premier couple et la forme oxydante NAD+ du second couple. rôle du catalyseur : un catalyseur accélère la vitesse d'une réaction. Il n'apparaît pas dans le bilan de la réaction. Lors du réglage initial, l'absorbance de la solution de référence avant toute mesure doit être réglée à zéro.
Le graphe est une droite : l'absorbance est proportionnelle à la oncentration 1 mL de solution D est placé dans une fiole jaugée de 50 mL que l'on complète avec de l'eau distillée : le facteur de dilution est 50 soit une dilution au 1/50e de la solution D. concentration massique en éthanol de l'échantillon étudié : Ce = Ae /k = 0,30 / 1,6 10-3 = 187 mg/L. concentration massique en éthanol de la solution D : Ce fois facteur de dilution = 187*50 = 9,37 103 mg/L = 9,37 g/L soit 9,37*0,2 = 1,87 g d'alcool dans le distillat issu de la distillation de 20 mL de vin. concentration massique en éthanol du vin : 1,87 / 0,02 = 93,7 g /L soit 9,37 g d'alcool dans 100 mL de vin volume d'alcool correspondant : masse (g) / masse volumique (g/mL) = 9,37 / 0,8 = 11,7 mL degré du vin : 11,7° arrondi à 12°. concentration molaire en acide malique restant dans le vin à l'instant t : concentration molaire (mol/L) = concentration massique (g/L) / masse molaire (g/mol) mlasse molaire de l'acide malique C4H6O5 : 12*4+6+5*16 = 134 g/mol d'où : concentration molaire en acide malique restant = Cm(t)/134 à t=0, Cm(t=0) = 3,5 g/L d'où C0= 3,5/134 =2,61 10-2 mol/L n acide malique (t = 0) initiale dans un litre de vin =2,61 10-2 mol
n acide malique (t) =2,61 10-2 -x soit x =2,61 10-2 -n acide malique (t).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Le Polonium est un élément métallique radioactif rare de symbole Po. Son numéro atomique est 84. Il a été trouvé dans un minerai, la pechblende, en 1898, par le chimiste français Pierre Curie, qui lui donna le nom de la patrie d'origine de son épouse : la Pologne. Le Polonium 210 est le seul isotope que l'on trouve dans la nature. La plupart des isotopes du Polonium se désintègrent en émettant des particules alpha. L'élément constitue donc une source de radiations alpha (a). (d'après http://www.ac-creteil.fr). Les notations a et 42He sont équivalentes. On donne un extrait de la classification périodique des éléments :
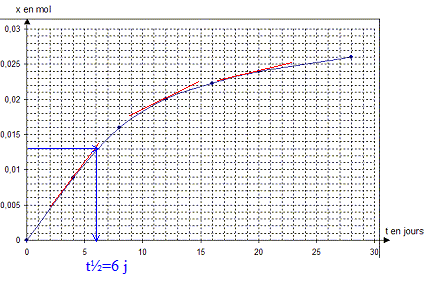
II - Deuxième partie : Soit N(t) le nombre de noyaux radioactifs d'un échantillon de Polonium, non désintégrés à la date t. A t = 0 on note N0 le nombre de noyaux radioactifs initial. Un détecteur de radioactivité a associé à un compteur à affichage numérique permet d'effectuer les mesures regroupées dans le tableau ci-dessous :
corrigé un noyau radioactif est un noyau instable qui par fusion ou fission conduit à un (des) noyau(x) plus stable(s) ; cela s'accompagne souvent de l'émision de radiations a, b ou g. composition du noyau de Polonium 210 : 84 protons et 210-84 = 126 neutrons. équation traduisant la désintégration de ce noyau 21084Po-->AZX+42He conservation de la charge : 84=Z+2 soit Z=82, donc X est identifié au plomb Pb conservation du nombre de nucléons : 210 = A+4 soit A= 206.
loi de décroissance du nombre de noyaux non désintégrés d'un échantillon contenant initialement N0 noyaux : N(t) = N0 exp(-lt) soit encore N(t) / N0= exp(-lt) ou -ln (N(t) / N0)= lt le graphe représentant -ln (N(t) / N0) en fonction du temps est une droite de coefficient directeur l : en accord avec la représentation graphique précédente. unité de l : 5 10-3 j-1 soit 5 10-3 /(24*3600)= 5,8 10-8 s-1. constante de temps t = 1 /l = 1/5,8 10-8 = 1,7 107 s. expression de la durée de demi-vie de l'échantillon : t1/2 = ln2 / l = ln2/5,8 10-8 = 1,2 107 s.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|