Cet exercice est un questionnaire à réponses ouvertes courtes. À chaque question peuvent correspondre aucune, une ou plusieurs propositions exactes.

Pour chacune des questions, chaque proposition doit être étudiée. Inscrire en toutes lettres " vrai " ou " faux " et donner une justification ou une explication.

Une réponse fausse ou une absence de réponse seront évaluées de la même façon.

Les parties 1 et 2 sont indépendantes et peuvent être traitées séparément.

I. Étude d'une corde de piano

On étudie le fonctionnement d'une corde de piano placée dans le dispositif simplifié (Figure 1).

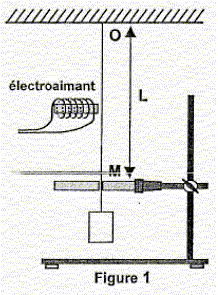
Accrochée à un support fixe en O, la corde est disposée verticalement. Elle passe en M par le trou d'un support tel que la corde soit immobile en ce point.

On note OM = L. La longueur L vaut 42,2 cm. À l'extrémité inférieure de la corde, est accrochée un solide de masse m.

Un électro-aimant, alimenté par un générateur basses fréquences délivrant une tension électrique sinusoïdale, permet d'exciter de façon sinusoïdale la corde à une fréquence f réglable. Les fréquences de vibration f qui interviennent dans cet exercice sont toujours celles de la corde. On fait varier la fréquence de vibration f de la corde de 200 à 2500 Hz.

À la fréquence f₀ = 523 Hz, on observe à la lumière du jour un fuseau unique de plus grande amplitude. On rappelle qu'une harmonique d'ordre n correspond à une fréquence propre de vibration de la corde donnée par n.f₀ où f₀ est la fréquence du mode fondamental de vibration de la corde et n un entier positif non nul.

1. À la fréquence f₀ = 523 Hz, on observe :
   - un ventre et deux nœuds ; vrai : n=1, mode fondamental : un ventre au centre et deux noeuds aux deux extrémités de la corde
   - un nœud et deux ventres ; faux
   - trois nœuds et deux ventres ; faux
   - un ventre et trois nœuds. faux
2. La fréquence f₀ = 523 Hz est la fréquence :
   - de l'harmonique d'ordre 1 ;faux
   - de l'harmonique d'ordre 2 ; faux
   - du mode fondamental. vrai mode fondamental : un ventre au centre et deux noeuds aux deux extrémités de la corde.
3. À la fréquence de vibration f₁ = 1046 Hz, on observe :
   - toujours 1 fuseau unique mais d'amplitude double ; faux
   - 2 fuseaux d'amplitudes importantes ; vrai, f₁= 2 f₀ ; n=2, donc deux fuseaux.
   - 2 nœuds. faux
4. La quantification des modes propres est donnée par la relation (avec n nombre entier) :
   - nl = 2L ; vrai
   - nl = L ; faux
   - nl =½L. faux
5. A la fréquence f₀ = 523 Hz, la célérité des ondes sur la corde vaut :
   nl = 2L ; n=1 donne l = 2L= 2*0,422 = 0,844 m pour f₀=523 Hz ; v=l f₀= 523*0,844 = 441 m/s.
   - 340 m.s^-1 ;
   - 3,00 10⁸ m.s^-1 ;
   - 441 m.s^-1 ;vrai
   - 221 m.s^-1.

II. Étude d'une corde placée dans un piano 

Les extrémités d'une corde placée dans un piano, sont reliées à une caisse de résonance en bois. L'expression de la célérité des ondes sur la corde en fonction de sa masse linéique (µ) et de sa tension (F) est : v = [F/µ]^½.

1. La caisse de résonance permet :
   - d'augmenter la hauteur du son produit par la corde ;faux
   - d'augmenter le niveau sonore du son ; vrai
   - d'entretenir les vibrations de la corde. faux
2. Pour augmenter la hauteur du son émis par la corde en vibration, il faut :
   augmenter la hauteur du son , c'est augmenter la fréquence f  ; or v = lf : il faut donc augmenter la célérité v et en conséquence la tension F.
   - tendre davantage la corde ; vrai
   - détendre la corde faux

III Étude de la note émise par un piano

1. Dans cette partie, on néglige tout phénomène d'amortissement. On étudie une corde de longueur L = 42,2 cm présente dans un piano, reliée à la touche " do4 " de l'instrument. Le pianiste en appuyant sur la touche " do4 " frappe cette corde par l'intermédiaire d'un marteau. Celle-ci oscille librement. On effectue l'enregistrement de la tension électrique u(t) aux bornes d'un microphone placé à côté de la corde oscillante à l'aide d'un dispositif d'acquisition informatisé. On obtient l'enregistrement simplifié (Figure 2) ci-dessous :
   
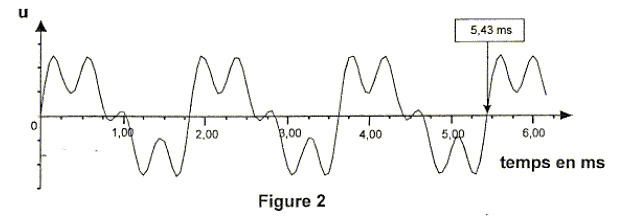
2. Le mode fondamental de la corde correspond à la fréquence
   184 Hz ; 276 Hz ; 552 Hz ; 1104 Hz .
   La période est voisine de 1,8 ms soit f₀= 1/1,8 10^-3 = 1000/1,8 voisin de 552 Hz
3. Le spectre de fréquence correspondant au son émis par la corde de piano est l'un des spectres proposés ci-dessous : (figures 3.a., 3.b., 3.c. ou 3.d.) où r est le rapport de l'amplitude de l'harmonique considéré sur l'amplitude de l'harmonique fondamentale.

   

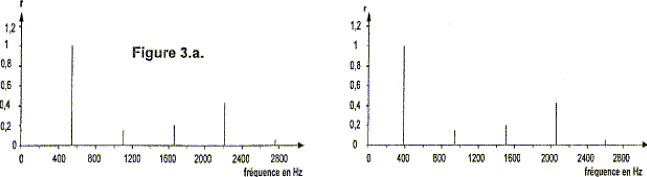
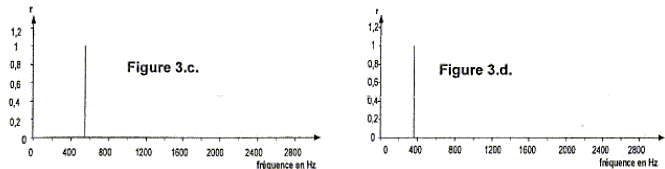
    Le son émis par la corde reliée à la touche " do4 " est un son complexe. A quelle figure correspond le spectre de fréquences ?
   Un son complexe posséde, en plus du fondamentale, des harmoniques. La fréquence du fondamental est 552 Hz : d'où figure 3a.

4. Le tableau ci-dessous récapitule les fréquences, en hertz, de notes de quelques cordes bien accordées du piano.

   si3	494	sol3	392	mi3	330	do3	262
   si4	988	sol4	784	mi4	659	do4	523
   si5	1976	sol5	1568	mi5	1318	do5	1046
   la3	440	fa3	349	ré3	294
   la4	880	fa4	698	ré4	587
   la5	1760	fa5	1397	ré5	1175

    Des réponses données précédemment, on peut affirmer que :
   - la corde étudiée est bien accordée ;faux
   - la corde étudiée est mal accordée.  vrai car la fréquence du fondamentale (552 Hz) est différente de la fréquence du do₄ (523 Hz)

    

   ---