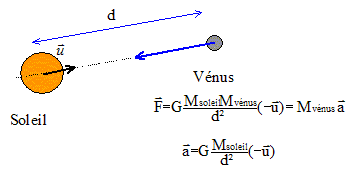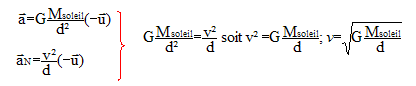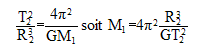|
marquage isotopique d'après bac France sept 2005 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Depuis plusieurs décennies, l'acide chlorhydrique et l'hypochlorite de sodium sont utilisés dans les piscines (1). L'acide chlorhydrique régule l'acidité ou le pH, tandis que l'hypochlorite désinfecte à merveille. Tous deux constituent des garanties pour notre santé. Non seulement l'eau de la piscine est désinfectée mais, en plus, l'hygiène et la propreté des conduites et des filtres sont maintenues sur l'ensemble de son parcours. L'hypochlorite de sodium est le désinfectant le plus utilisé. Les grandes piscines le stockent en vrac dans de grandes citernes, les plus petites dans des fûts. Exceptionnellement, on rencontre une installation qui prépare ce produit sur place. Cela s'effectue par électrolyse de la saumure (solution aqueuse de chlorure de sodium), dont résulte du chlore gazeux. Après mélange avec de l'hydroxyde de sodium en solution, on obtient de l'hypochlorite de sodium. D'après Le livre blanc du chlore, juillet 2003 (www.belgochlor.be) (1) En milieu beaucoup plus acide que l'eau de la piscine, les ions hypochlorite et chlorure réagissent et donnent un dégagement de dichlore, gaz toxique.
Les parties 1 et 2 traitent de la fabrication de I'hypochlorite de sodium par électrolyse d'une solution de chlorure de sodium. La partie 3 traite du principe de la régulation du pH d'une eau de piscine. Cette partie est indépendante des parties 1 et 2.
Pour déterminer les produits de l'électrolyse d'une solution de chlorure de sodium, on réalise l'expérience suivante au laboratoire (voir schéma simplifié de laFigure 1 ci-dessous). Un tube en U contient une solution de chlorure de sodium (Na+(aq) + Cl-(aq) ). Deux électrodes A et B sont reliées chacune à l'une des bornes (positive ou négative) d'un générateur de tension continue G. Après plusieurs minutes de fonctionnement, on effectue des tests d'identification des produits formés. - À une électrode, il s'est formé un dégagement de dichlore. - À l'autre électrode, il s'est formé un dégagement de dihydrogène et il est apparu des ions hydroxyde HO -. L'équation de la réaction modélisant l'électrolyse est : 2 H2O + 2 Cl - (aq) = H2 (g) + Cl2 (g) + 2 HO -(aq) (équation 1) 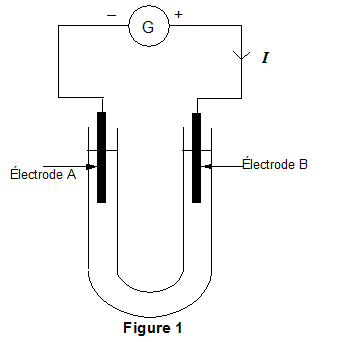
Données : couples oxydant/réducteur : H2O / H2 (g) ; Cl2 (g) / Cl -(aq) ; O2 (g) / H2O ; ClO - (aq) / Cl2 (g)
corrigé À une électrode, il s'est formé un dégagement de dichlore : Cl2 (g) /Cl - (aq) : oxydation des ions chlorure, à l'anode positive B suivant : 2Cl - (aq)= Cl2 (g) + 2e-. À l'autre électrode, il s'est formé un dégagement de dihydrogène et il est apparu des ions hydroxyde HO -: H2O / H2 (g) : réduction de l'eau à la cathode négative A suivant : 2 H2O + 2e-= H2 (g) +2 HO -(aq)
2Cl - (aq)= Cl2 (g) + 2e- donne : n(e -) = 2n1(Cl2 ) Cl2 (g) + 2 HO - (aq) = ClO - (aq) + Cl - (aq) + H2O (équation 2) relation entre la quantité n(ClO-) d'ions hypochlorite formés et la quantité n2(Cl2) de dichlore consommé dans la réaction d'équation 2 : n2(Cl2) = n(ClO-) d'après les coefficients stoechiomètriques relation entre n(e -) et n(ClO- ): au fur et à mesure que le dichlore se forme il réagit avec les ions hydroxydes pour conduire aux ions hypochlorites, donc : n1(Cl2 ) =n2(Cl2)
= ½ n(e -)=n(ClO-) Q= I Dt = NA.e n(e -) soit : n(e -) =I Dt /( NA.e )= 20*3600/ 105 =0,72 mol n(ClO-) =½ n(e -)= 0,36 mol. espèce prédominante du couple HClO(aq)/ClO -(aq) à pH=8,5 : le pH étant supérieur au pKa du couple HClO(aq)/ClO -(aq), la forme basique ClO -(aq) prédomine à pH=8,5 rapport des concentrations en ions hypochlorite et en acide hypochloreux : pH= pKa3 + log ([ClO -]/[HClO] soit log ([ClO -]/[HClO] )= pH- pKa3 = 8,5-7,5 = 1 ; [ClO -]/[HClO] = 10. ClO -(aq) + H3O+(aq) = HClO(aq) + H2O (équation 3). constante d'équilibre K de cette réaction en fonction de Ka3 : K= [HClO]éq/ ([ClO -]éq [H3O+]éq ) or Ka3 = [ClO -] [H3O+] /[HClO] d'où K= 1/ Ka3 = 1/ 10-7,5 = 107,5. concentration molaire effective initiale en ions H3O+ notée [H3O+]i = Qté de matière initiale d'ion oxonium (mol) / volume de la piscine (L) = 0,1/105 = 10-6 mol/L. quotient de réaction initial Qr,i =[ClO -]i
[H3O+]i /[HClO]i = 10 * 10-6
= 10-5. À partir de l'expression de la constante d'acidité Ka3 du couple acide hypochloreux/ion hypochlorite et du rapport [ClO -]i/[HClO]i calculé, montrer que le pH de l'eau de la piscine diminue d'une part Ka3 = [ClO -] [H3O+] /[HClO] soit [H3O+] = Ka3 [HClO] / [ClO -] d'autre part ClO -(aq) + H3O+(aq) = HClO(aq) + H2O est totale donc n(ClO -) diminue de 0,1 mol et n(HClO) augmente de 0,1 mol en conséquence le rapport [HClO] /[ClO -] augmente Ka3 étant constant à température constante, alors [H3O+] augmente et le pH diminue.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
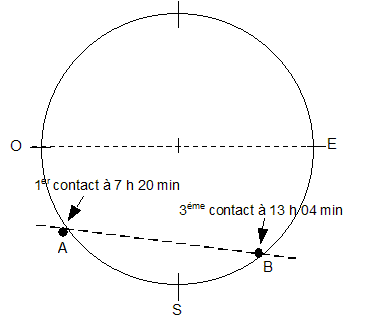
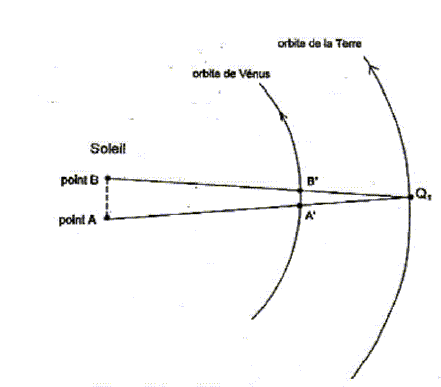
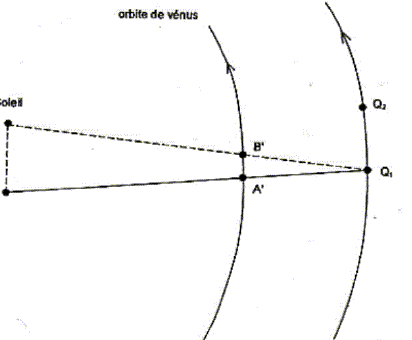
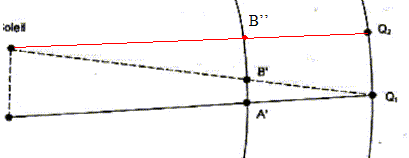
Le transit d'une planète correspond à son passage entre la Terre et le Soleil. Pour un observateur terrestre cela se manifeste par la présence d'un disque sombre sur le fond brillant du Soleil. Les transits de Vénus sont des phénomènes extrêmement rares. On compte en effet environ 2 passages de Vénus devant le Soleil par siècle, mais aucun transit n'a eu lieu au cours du 20ème siècle. Au 19ème siècle les passages de la planète devant le disque solaire ont eu lieu en 1874 et en 1882. Au 21ème siècle, le même phénomène s'est reproduit très récemment le 8 juin 2004. Le prochain transit de Vénus aura lieu le 6 juin 2012 mais il ne sera pas observable depuis la France. La figure ci-dessous est un montage photographique réalisé, en France, par un astronome amateur. On voit sur le même cliché quelques positions de ce transit.  À partir de ce cliché et des données astronomiques fournies, l'astronome amateur désire mesurer la vitesse orbitale de Vénus. Quelques données astronomiques : Soleil : Masse M1 = 2,0 10 30 kg ; distance moyenne à la Terre R1 = 1,5 10 8 km ; Diamètre D1 = 1,4 x10 6 km Vénus : Distance moyenne au Soleil R2 = 1,0 108 km Masse notée M2 Constante de la gravitation : G = 6,6 1011 SI Pour les applications numériques il faut choisir dans les aides fournies la valeur appropriée au résultat attendu.
Le mouvement de la planète Vénus est uniforme. Donc le vecteur accélération de Vénus est centripète, dirigé vers le centre du soleil, origine du repère d'étude. expression de la vitesse de cette planète :
avec d=R2 = 1011 m ; v2= (6,6 10-11*2 1030/1011)½=(6,6*2 108)½=3,6 104 m/s. La période T2 est la durée que met Vénus pour décrire une circonférence de rayon R2 à la vitesse v2. 2pR2=v2T2 soit 2pd=vT Elever au carré : ( on note simplement v la vitesse, T la période et d le rayon de l'orbite.) 4p²d²=v²T² remplacer v² par son expression : v²= GMsoleil/d 4p²d²= GMsoleilT²/d ; 4p²d3= GMsoleilT² ; T²= 4p²d3 / (GMsoleil) T= 2p[d3 / (GMsoleil)]½ T=2p[1033 / (6,6 10-11*2 1030)]½=2p[1033 / (6,6 *2 1019)]½=2p[1014 / 13,2]½ T=2p 107/3,6 = 1,7 107 s. 3ème loi de Kepler : T²= 4p²d3 / (GMsoleil) peut s'écrire : T² / d3 = 4p² / (GMsoleil)
distance AB à la surface du disque solaire de diamètre D1 = 1,4 x10 6 km AB=0,75 OE = 0,75 D1 = 0,75*1,4 x10 6 = 1,05 106 km. vitesse de Vénus déterminée à partir de la figure n°7 A'B'/ AB = A'Q1/AQ1 soit A'B' = AB*A'Q1/AQ1 avec A'Q1= R1-R2 = 1,5 108-108 = 0,5 108 km et AQ1 = R1= 1,5 108 km A'B' = 1,05 106 *0,5 108 / ( 1,5 108) = 1,05 106 /3 = 0,35 106 km vitesse (km/s) = distance (km)/ durée (s) = 0,35 106 / ( 2 104) = 35/2 = 17,5 km/s. distance Q1Q2 parcourue par la Terre sur son orbite pendant la durée tAB : Q1Q2 (km) = vitesse (km/s) * durée (s) = 30 * 2 104 = 6 105 km. Q1Q2 est du même ordre de grandeur que la distance AB , mais Q1Q2 est trés inférieure à R1 : donc la Terre peut être considérée immobile durant cette période. À chaque instant la position de la Terre, celle de Vénus et celle de la tache repérée sur le disque solaire sont alignées.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Le marquage isotopique consiste à remplacer dans la molécule
que l'on désire étudier, un atome ou un groupe d'atomes par un atome
radioactif de manière à pouvoir l'utiliser comme traceur. Dans cet
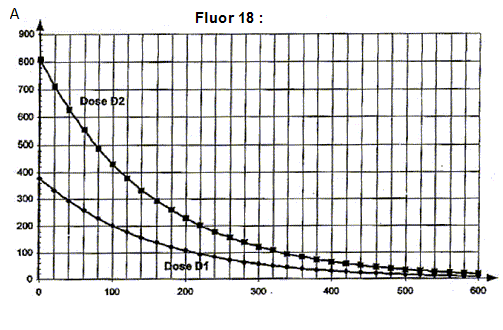
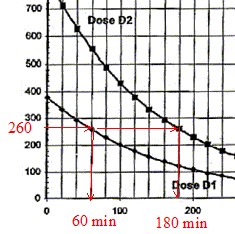
exercice on s'intéressera à deux applications de cette technique : Les parties 1 et 2 sont indépendantes 1. Marquage isotopique et technique d'imagerie médicale En cancérologie, le traceur utilisé pour l'imagerie médicale est le glucose marqué par le fluor 18. Ce traceur s'accumule préférentiellement dans les cellules cancéreuses, grandes consommatrices de sucre. Cette technique se singularise par l'utilisation d'isotopes radioactifs dont le temps de demi-vie est beaucoup plus court que les produits classiques de la médecine nucléaire. Ainsi le fluor 18 a un temps de demi-vie radioactive de 110 minutes. Pour cette raison le traceur est fabriqué sur place de manière à ce qu'au moment de son injection au patient la dose administrée ait une activité de 260 MBq.
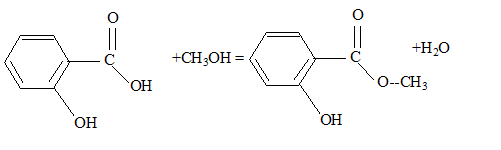
Utilisation du marquage isotopique en chimie Le salicylate de méthyle est le composant principal d'une huile essentielle naturelle appelée essence de wintergreen extraite par hydrodistillation des feuilles de gaulthérie, bruyère d'Amérique du Nord et de Chine. Doté d'une odeur caractéristique, il confère à cette huile essentielle des propriétés analgésique et anti-inflammatoire puissantes. Appliqué par voie cutanée sous forme de pommade, il est très apprécié des sportifs tant avant qu'après l'effort. Pour des raisons économiques le salicylate de méthyle est à l'heure actuelle synthétisé à partir de l'acide salicylique et du méthanol.
corrigé composition du noyau de l'isotope 18 du fluor : 9 protons et 18-9 = 9 neutrons 189F-->188O+ AZX conservation de la charge : 9=Z+8 soit Z=1 conservation du nombre de nucléons : 18=18+A soit A=0 AZX est un positon, en conséquence type de radioactivité b+. définition du temps de demi-vie radioactive : durée au bout de laquelle la moitié des noyaux initialement présents se sont désintégrés. Par une analyse dimensionnelle, déterminer l'unité de l : lt½=ln2: ln2 est sans dimension, en conséquence l est l'inverse d'un temps ; l s'exprime en seconde-1. or, d'après le texte t½=110 minutes = 110*60 = 6,6 103s. l= ln2 / (6,6 103)=
0,69/(6,6 103) voisin de 10-4 s-1.
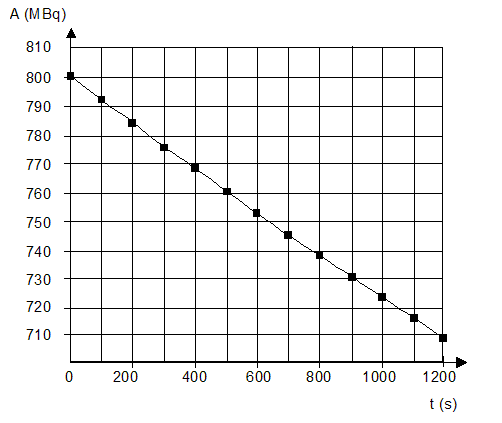
or A= - dN/dt, dériver N(t) par rapport au temps : dN(t)/dt = N0.(-l)exp(-lt). d'où l'activité A de la source radioactive : A = N0lexp(-lt) = A0.exp(-lt) avec A0=N0l. nombre de noyaux de " fluor 18 " présents dans la dose de traceur au moment de son injection au patient A0= = 260 MBq = 260 106 Bq= 2,6 108 Bq ; l= 10-4 s-1. N0=A0/ l= 2,6 108 /10-4 =2,6 1012 noyaux.
l'heure de la fabrication de la dose de traceur notée D1 est 8 heures ( injection à 9 h) l'injection de la dose notée D2 préparée en même temps que la dose D1 a lieu à 11h, l'activité de celle-ci devant être égale à 260 MBq. temps nécessaire après l'injection pour que l'activité soit 100 fois plus faible qu'au moment de l'injection. A0= 260 MBq ; A(t) = 2,6 MBq ; A = A0exp(-lt) ; ln (A0/A)= lt t = ln (A0/A)/ l= ln100
/ 10-4 = 4,6 104 s = 4,6 104/3600 =
46/3,6=13 heures.
d'autre part : DA(tn)/Dt + l A(tn)=0 soit DA(tn) = -l A(tn)Dt A(tn+1) = A (tn) -l A(tn)Dt = (1-lDt ) A(tn) activité A(t1) à l'instant de date t1 = 100 s et la valeur de l'activité A(t2) à l'instant de date t2 = 200 s A(t1)= (1-lDt ) A(t0) = (1-10-4*100)*800 = 0.99*800=792 MBq A(t2)= (1-lDt ) A(t1) = (1-10-4*100)*792 = 0.99*792=784 MBq ces valeurs sont en accord avec celles lues sur le graphe. l'intérêt et l'inconvénient du choix d'un pas de résolution Dt = 1 s : la courbe obtenue à partir de la
méthode d'Euler se superpose à la courbe expérimentale ( avantage) mais
le nombre de calculs est très important ( inconvénient)
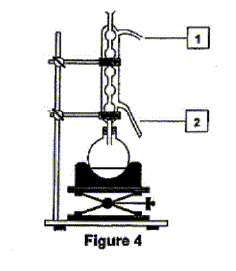
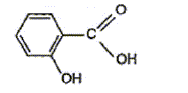
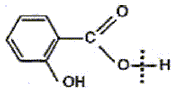
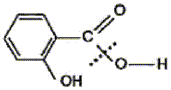
éstérification, lente, athermique, limitée par l'hydrolyse de l'ester L'acide sulfurique joue le rôle de catalyseur (2) entrée de l'eau dans le réfrigérant droit ; (1) sortie de l'eau du réfrigérant. Le chauffage à reflux permet d'accélérer la réaction en travaillant à température modérée, tout en évitant les pertes de matière des réactifs et des produits ( les vapeurs qui se dégagent se condensent et retombent dans le mélange réactionnel) Qtés de matière initiales des réactifs (mol) = masse (g) / masse molaire (g/mol) acide salicylique : 69/138 = 0,5 mol : méthanol : 32/32 = 1 mol D'après les coefficients de l'équation bilan une mole d'acide réagit avec une mole d'alcool : en conséquence l'acide salicylique est en défaut. La réaction étant limitée, en ajoutant l'un des réactifs en excès ( celui qui coûte le moins cher) on déplace l'équilibre vers la formation de l'ester( ainsi le rendement va augmenter). Hypohhèse 1 : d'après les coupures indiquées, l'atome d'oxygène radioactif 18O se retrouvera dans la molécule d'eau, ce qui est en désaccord avec les observations expérimentales citées dans le texte. Hypohhèse 2 : d'après les coupures indiquées, l'atome d'oxygène radioactif 18O se retrouvera dans la molécule d'ester et non pas dans l'eau ce qui est en accord avec les observations expérimentales citées dans le texte.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|