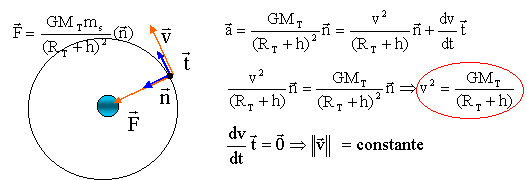|
titrage et indicateurs colorés d'après bac France 2005 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Passionné d'astronomie, un élève a collecté sur le réseau Internet de nombreuses informations concernant les satellites artificiels terrestres. Il met en œuvre ses connaissances de physique pour les vérifier et les approfondir. Dans tout l'exercice, on notera : Masse de la Terre : MT (répartition de masse à symétrie sphérique de centre O) ; rayon de la Terre : RT ; masse du satellite étudié : mS ; altitude du satellite étudié : h ; constante de gravitation universelle : G Les questions 2 et 3 sont indépendantes. 1. Le premier satellite artificiel. Si la possibilité théorique de mettre un satellite sur orbite autour de la Terre fut signalée en 1687 par Isaac Newton, il a fallu attendre le 4 octobre 1957 pour voir le lancement du premier satellite artificiel, Spoutnik 1, par les soviétiques.
2. Les satellites artificiels à orbites circulaires. Le télescope spatial Hubble, qui a permis de nombreuses découvertes en astronomie depuis son lancement en 1990, est en orbite circulaire à 600 km d'altitude et il effectue un tour complet de la Terre en 100 minutes..1. Etude du mouvement du satellite Hubble dans un référentiel géocentrique
3. Les satellites artificiels à orbites elliptique. Les satellites peuvent être placés sur différentes orbites, en fonction de leur mission. Un incident lors de leur satellisation peut modifier l'orbite initialement prévue. Hipparcos, un satellite d'astrométrie lancé par la fusée Ariane le 8 août 1989, n 'a jamais atteint son orbite prévue. Un moteur n'ayant pas fonctionné, il est resté sur une orbite elliptique entre 36 000 km et 500 km d'altitude.
4. Les missions des satellites artificiels. Aujourd'hui plus de 2 600 satellites gravitent autour de la Terre. Ils interviennent dans de nombreux domaines : téléphonie, télévision, localisation, géodésie, télédétection, météorologie, astronomie. Leur spectre d'observation est vaste, optique, radar, infrarouge, ultraviolet, écoute de signaux radioélectriques.
corrigé Le satellite est soumis à la seule force de gravitation exercée par la terre, force centripète, dirigée vers le centre de la terre. Ecrire la seconde loi de Newton suivant l'axe n, pour obtenir l'accélération centripète, de valeur v²/(RT+h)
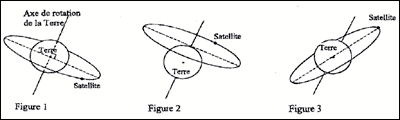
La force centripète, perpendiculaire à la vitesse, ne travaille pas ; en conséquence l'énergie cinétique du satellite n'est pas modifiée et la valeur de la vitesse est constante : le mouvement circulaire est donc uniforme. Le satellite parcourt une circonférence 2p(RT+h) à la vitesse v, de valeur constante durant une période T 2p(RT+h) = v T élever au carré puis remplacer v² par GMT/(RT+h) 4p2(RT+h)2 = v2 T2 ; 4p2(RT+h)2 = GMT/(RT+h)T2 ; T= 2p((RT+h)3/ GMT) ½. T2 /(RT+h)3 =4p2/ GMT. ( 3ème loi de Kepler) un satellite géostationnaire tourne dans le même sens que la terre, dans le plan équatorial ; ce satellite a la même vitesse de rotation que la terre, en conséquence, pour un observateur terrestre il paraît fixe. figure 2 : incompatible avec les lois de la mécanique. Le satellite doit se déplacer sur une ellipse dont la terre doit être l'un des foyers, ce qui n'est pas le cas sur la figure 2. (ou encore d'après la première loi de Kepler le plan de la trajectoire du satellite doit contenir le centre de la Terre) figure 3 : le satellite ne reste pas à la verticale d'un même point de la surface de la terre, lorsque celle-ci tourne autour de son axe. figure 1 : la trajectoire correspond au satellite
géostationnaire.
loi n°1 : dans le référentiel géocentrique ( dans ce cas) la trajectoire du centre d'un satellite est une ellipse dont la terre est l'un des foyers. loi n°3 : tous les satellites en orbite autour d'un astre ( ici la terre) sont tels que le rapport entre le carré de la période de révolution et le cube du demi-grand axede l'éllipse est constant T2/a3= cte.
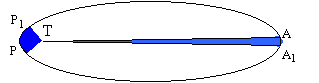
loi des aires : le satellite passe de P à P1 et de A à A1 pendant la même durée : aire S1= aire S2. Or PT<AT donc arc PP1> arc A A1, en conséquence la vitesse du satellite est plus grande près de P que près de A. La vitesse du satellite varie. en P ( plus proche de la terre que A ) la vitesse est maximale
et en A la vitesse est minimale.
les limites des longueurs d'onde dans le vide de ce spectre : 400 nm : limite entre le visible et les UV ; les longueurs d'onde des UV sont inférieures à 400 nm. 800 nm : limite entre le visible et l'infrarouge IR ; les longueurs d'onde de l'infrarouge sont supérieures à 800 nm les limites en fréquence de la lumière visible. f1 = c/l1= 3 108 / 4 10-7 = 7,5 1014 Hz. f2 = c/l2= 3 108 / 8 10-7 = 3,7 1014 Hz. On doit préciser "dans le vide" pour donner des valeurs de longueur d'onde : la longueur d'onde dépend du milieu où l'onde se propage ( seule la fréquence de l'onde est constante lors d'un changement de milieu).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
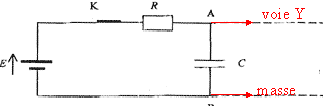
Un élève, dans le cadre de travaux personnels, souhaite étudier un système d'alarme. Après avoir modélisé la mise sous tension du circuit de commande de la sirène (première partie de l'exercice), il cherche à savoir si des phénomènes inductifs peuvent provoquer le déclenchement intempestif de la sirène (deuxième partie de l'exercice). I. Première partie : fonctionnement simplifié d'une alarme d'appartement Après avoir mis sous tension l'alarme d'un appartement, il faut pouvoir disposer d'une durée suffisante pour sortir sans la déclencher. Pour cela certains dispositifs utilisent la charge et la décharge d'un condensateur. Le circuit est alimenté par une batterie d'accumulateurs de force électromotrice (f.e.m.) E. Le schéma simplifié de l'alarme est le suivant. 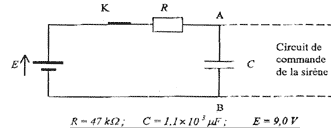 La mise sous tension de l'alarme correspond à la fermeture de l'interrupteur (K). Le circuit de commande de la sirène est tel qu'à la fermeture de la porte de l'appartement, le condensateur est mis en court-circuit (ses armatures sont alors reliées par un fil conducteur non représenté sur le schéma).
Deuxième partie : l'alarme
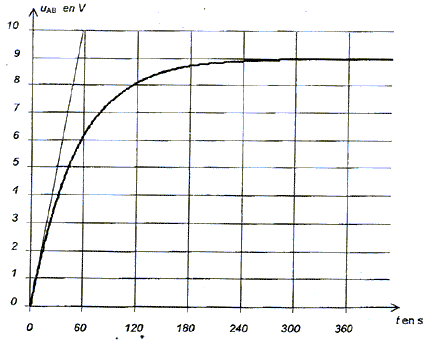
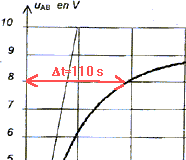
peut-elle se déclencher de manière intempestive ? 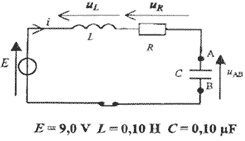 L'élève enregistre comme dans la première partie de l'exercice la tension uAB = f(t) aux bornes du condensateur, pour deux valeurs de résistance R1 = 160 W et R2 = 2,4 kW . Il obtient les courbes a et b ci-dessous. 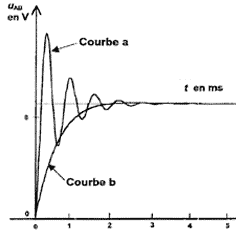
corrigé
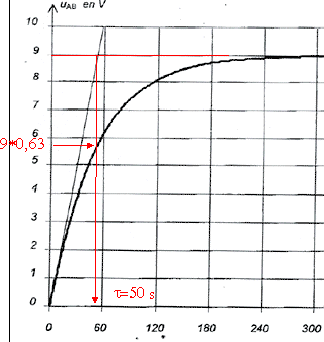
L'intersection de la tangente à l'origine avec l'asymptote donne un point dont l'abscisse est la constante de temps. ou bien tracer une horizontale d'ordonnée 0,63*9 = 5,7 V ; à partir de l'intersection avec la courbe tracer la verticale.
t= RC = 47 103 * 1,1 10-3 = 52 s.( valeur est compatible avec celle trouvée graphiquement )
En fermant la
porte, le condensateur est mis en court-circuit : la tension à ses
bornes s'annule. La tension aux bornes du condensateur ne pouvant plus
atteindre 8V ( seuil de déclenchement de l'alarme), l'alarme ne se
déclenche pas tant que la porte reste fermée.
courbe a : régime pseudopériodique ; la résistance R n'est pas très élevée (R1 = 160 W). courbe b : régime apériodique ; la résistance R n'est élevée (R2 = 2400 W). l'intensité du courant dans le circuit s'annule à partir de t = 4 ms : la charge q du condensateur est éagle à : q= C uAB. l'intensité est égale à la dérivée de la charge par rapport au temps : i = dq/dt = C duAB/dt duAB/dt correspond au coefficient directeur de la tangente à la courbe uAB=f(t) pour une date donnée. les courbes a et b se rapprochent de l'horizontale vers t= 4 ms : à partir de cette date, la tangente aux courbes a et b est horizontale ( coefficient directeur nul) et en conséquence l'intensité s'annule. valeur finale de la tension uAB : uAB+uR+uL=E uR= Ri avec ifin=0 donc uR s'annule. uL= Ldi/dt avec ifin =0 soit difin/dt = 0 et uL=0. en conséquence uAB=E= 9 V au dela de t = 4 ms. Dans le cas de la courbe (a), la tension uAB dépasse plusieurs fois la valeur limite de déclenchement de l'alarme : celle-ci se déclenche par intermittence. calcul de ½R(C/L)½>=1 avec C= 1,1 10-3 F ; L= 10-3 H ; R= 4,7 104 W. 0,5*4,7 104 (1,1)½ = 2,5 104, valeur bien supérieure à 1 : donc il n'y a pas d'oscillations.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La première utilisation d'un indicateur coloré pour les titrages acido-basiques remonte à 1767 par W. Lewis. Il employait un extrait de tournesol (...). On utilisait à l'époque des extraits de plantes qui changent de couleur avec l'acidité du milieu (...). On peut en citer quelques-uns parmi les plus connus et les meilleurs : l'artichaut (...) , la betterave rouge (...) , le chou rouge, de loin l'extrait le plus intéressant car sa couleur change nettement suivant la valeur du pH :
1. Des indicateurs colorés en cuisine. Le chou rouge est un légume riche en fibres et en vitamines, qui se consomme aussi bien en salade que cuit. Mais la cuisson du chou rouge peut réserver des surprises : chou rouge et eau de cuisson deviennent rapidement bleus. Pour rendre au chou sa couleur violette, on peut ajouter un filet de citron ou du vinaigre. Après avoir égoutté le chou, une autre modification de couleur peut surprendre le cuisinier : versée dans un évier contenant un détergent, l'eau de cuisson devient verte. En utilisant les textes ci-dessus :
2. Des indicateurs colorés pour les titrages. De nos jours, les indicateurs colorés sont toujours largement utilisés pour les titrages. La pH-métrie est une autre technique de titrage acido-basique qui permet en outre de choisir convenablement un indicateur coloré acido-basique pour ces mêmes titrages. Dans la suite de l'exercice, on s'intéresse au titrage de l'acide éthanoïque de formule CH3-CO2H (noté par la suite HA) contenu dans un vinaigre commercial incolore. La base conjuguée de cet acide sera notée A-.
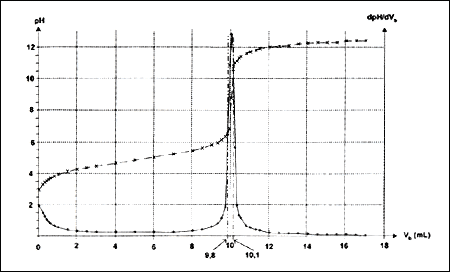
corrigé Un indicateur coloré acido basique est constitué par un couple acide/base dont la forme acide et la forme basique ont des couleurs différentes. Le vinaigre est acide : le chou est violet en présence de vinaigre. Le détergent est basique : le chou est vert en sa présence du détergent. Le facteur de dilution vaut 10 : volume fiole jaugée (mL) / volume pipette jaugée (mL) = 10. don pipette jaugée 20,0 mL et fiole jaugée 200,0 mL. réaction du titrage : CH3COOH + HO- --> CH3-COO- + H2O, réaction totale D'après la
courbe, VBE est proche de 10 mL. Si VB = 6 mL, la
quantité de matière d'ions HO- versé à la burette est donc
inférieure à celle de l'acide HA : l'ion HO- est le réactif
limitant.
d'après la courbe le pH est voisin de pH=5 après avoir ajouté 6 mL de soude. [H3O+]f= 10-pH = 10-5 mol/L. [HO-] f = 10-14 / [H3O+]f= 10-14 /10-5 = 10-9 mol/L le volume du mélange est : 10+60 +6 = 76 mL= 7,6 10-2 L Qté de matière ion hydroxyde : (mol) = volume solution (L) * concentration (mol/L) n(OH-)f =7,6 10-2 *10-9=7,6 10-11 mol. xf = n(OH-)0 - n(OH-)f = 6 10-4 - 7,6 10-11 = 6 10-4 mol taux d'avancement
final : t = xf / xmax
= 1; la réaction est totale.
On peut aussi utiliser la méthode des tangentes. A l'équivalence, n(HA)0 = n(HO-) versé à l'équivalence : Ca Va = Cb VBE Ca = Cb VBE / Va = 0,1* 10 / 10 = 1,0.10-1 mol / L en tenant compte
de la dilution : C0 = 10 Ca = 1,0 mol.L-1.
logKi = log[A-ind]éq/[HAind]éq+ log[H3O+]éq log[A-ind]éq/[HAind]éq=logKi-log[H3O+]éq=pH-pKi. [A-ind]éq/[HAind]éq= 10pH-pKi. Pour l'artichaut : VB = 9,8 mL, [A-ind]éq/[HAind]éq = 106,5 – 7,5 =0,1 VB = 10,1 mL, [A-ind]éq/[HAind]éq = 1010,5 – 7,5 =103.
L'artichaut est l'indicateur adapté. Si le vinaigre est coloré, alors il masque le virage de l'incolore au jaune de l'indicateur.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||