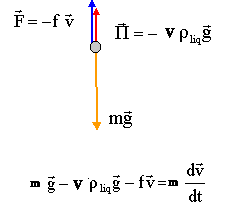|
viscosité
d'une huile moteur ;
hydrolyse
basique des esters ; diapason électronique
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
viscosité
d'une huile moteur : 5,5 points .
Dans les moteurs à combustion, on minimise les frottements
entre les pièces mécaniques en utilisant des huiles afin d'obtenir un
frottement visqueux. Plus une huile est épaisse, plus sa viscosité est
élevée. On souhaite déterminer expérimentalement la viscosité d'une
huile moteur. Pour cela on filme la chute verticale d'une balle dans
cette huile moteur avec une caméra numérique. L'exploitation du film
avec un ordinateur permet de déterminer les valeurs de vitesse de la
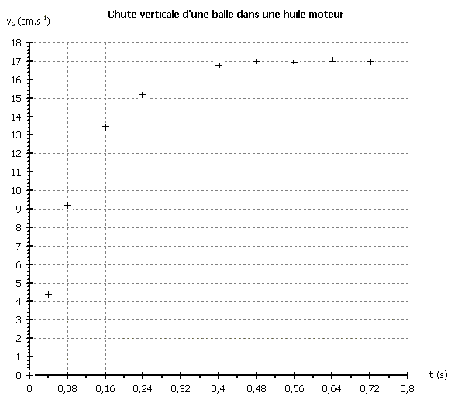
balle en fonction du temps. On obtient le graphe suivant :
- Validité de la modélisation de la force de frottement
Pour étudier le mouvement de la balle, on se place dans le référentiel
du laboratoire. On prendra l'axe vertical Oz dirigé vers le bas. Les
caractéristiques de la balle sont : masse m = 35,0 g ; rayon R = 2,00
cm ; volume V = 33,5 cm3 . La masse volumique de l'huile est
rhuile = 0,910 g.cm-3
.
On suppose que la force de frottement s'exprime sous la forme f = - kv
( les vecteurs sont écrits en bleu et en gras)où est la vitesse
du centre d'inertie de la balle. On appellera vG
la composante de la vitesse suivant l'axe Oz.
- Faire l'inventaire des forces extérieures appliquées à la balle en
chute libre verticale dans l'huile, puis les représenter sur un schéma.
- En appliquant la deuxième loi de Newton, établir l'équation
différentielle du mouvement de la balle dans le référentiel du
laboratoire.
- Montrer que dvG/dt peut se
mettre sous la forme : dvG/dt =
A - B×vG. avec A = g×(1 -rhuileV/m ) et B = k/m .
-Vérifier que la constante A = 1,27 S.I. en précisant son unité. On
donne la valeur du champ de pesanteur g = 9,81 m.s-2 .
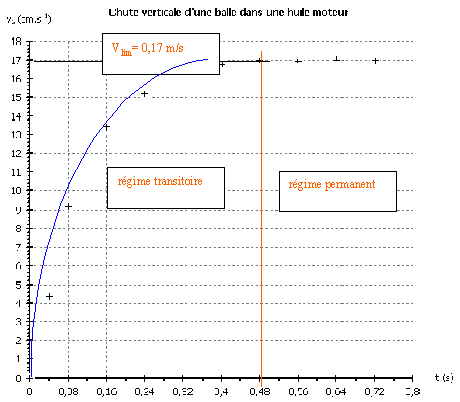
- Le mouvement de chute de la balle présente deux régimes visibles sur
la représentation graphique vG = f(t) donnée. 1. * Séparer,
sur le graphe par un axe vertical les domaines des deux régimes. On
précisera le domaine du régime permanent et le domaine du régime
transitoire du mouvement de la balle.
* Relever la valeur de la vitesse limite vlim sur la représentation
graphique vG = f(t).
* Que vaut l'accélération de la balle quand celle-ci atteint la vitesse
limite ?
- Connaissant la constante A donnée et la constante B = 7,5 s-1,
la méthode d'Euler permet d'estimer par le calcul la valeur de la
vitesse de la balle en fonction du temps en utilisant les deux
relations :
dvG(ti)/dt = A - B×vG(ti) et vG(ti+1) = vG(ti) + dvG(ti)/dt Dt où D t est le pas
d'itération.
Nous obtenons le tableau de valeurs suivant :
|
t(s)
|
0
|
0,080
|
0,16
|
0,24
|
0,32
|
0,40
|
0,48
|
0,56
|
|
dvG/dt
(m/s²)
|
?
|
0,51
|
0,20
|
?
|
0,03
|
0,02
|
0
|
0
|
|
vG (m/s)
|
0
|
0,102
|
0,143
|
?
|
0,165
|
0,167
|
0,169
|
0,169
|
* Quel est le pas d'itération de la méthode d'Euler proposée ?
* Que vaut l'accélération à l'instant t = 0 s ?
* En utilisant la méthode d'Euler calculer la valeur de la vitesse à
l'instant t = 0,24 s ; en déduire la valeur de l'accélération à
l'instant t = 0,24 s.
* Placer sur la représentation vG = f(t) les valeurs des
vitesses obtenues par la méthode d'Euler et tracer la courbe passant
par ces points.
- Sur quel paramètre peut-on agir pour améliorer la résolution de
l'équation différentielle par la méthode d'Euler ? En comparant la
courbe obtenue par la méthode d'Euler et les points expérimentaux, la
modélisation de la force de frottement de l'huile sur la balle f= - k× v
est-elle valide ? Justifier votre réponse.
- Détermination de la viscosité de l'huile moteur
Pour des vitesses faibles, la formule de Stokes permet de modéliser la
force de frottement fluide agissant sur un corps sphérique en fonction
de la viscosité h de l'huile, du rayon de
la balle R et de la vitesse de déplacement vG
de la balle telle que : f= - 6 ph R vG
avec h en Pa.s, R en m et vG en
m.s-1 .
- En vous aidant de l'expression de B donnée à la question 1.3 et de
l'hypothèse f = - k×vG , exprimer la viscosité h en fonction de B, m et R.
- Calculer la viscosité h de l'huile
étudiée.
À l'aide des valeurs de viscosité données ci-dessous, identifier
l'huile de moteur étudiée.
|
Huile moteur à 20°C
|
|
SAE 10
|
SAE 30
|
SAE 50
|
|
h(Pa.s)
|
0,088
|
0,290
|
0,700
|
corrigé
La bille est soumise à son poids, verticale
vers le bas, valeur mg
à la poussée
d'Archimède, verticale vers le haut, valeur rliq Vg
à la force de
frottement fluide, colinéaire à la vitesse, de sens contraire, valeur
f= kv.
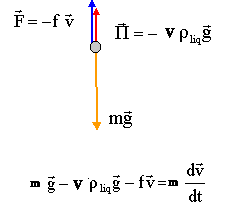
suivant un axe
vertical, orienté vers le bas, la seconde loi de Newton s'écrit :
mg-Vrliq g - kvG = mdvG/dt
dvG/dt
= g -Vrliq g/m - k/mvG
; dvG/dt =g(1-Vrliq /m) -k/mvG
A= g(1-Vrliq /m) ; B= k/m
valeur de A:
g= 9,81 m/s² ; V= 33,5 10-6 m3 ; rliq = 910 kg m-3 ; m= 35
10-3 kg
A= 9,81*(1-33,5 10-6
*910/35 10-3)=1,27 m/s²
A a la dimension
d'une accélération car le terme Vrliq
/m, ajouté au nombre 1, est sans dimension.
Lorsque la
vitesse limite est atteinte, la vitesse est constante (mouvement
rectiligne uniforme) et en conséquence l'accélération , dérivée de la
vitesse par rapport au temps, est nulle.
Le pas de
résolution est Dt= 0,08 s
à t=0 : [dvG/dt]t=0 = A-BvG(t=0) = A-B*0=A= 1,27 m/s².
à t=0,24 s : [dvG/dt]t=0,24 = 1,27 - 7,5×vG(t=0,24)
et vG(t=0,24)
= vG(t=0,16) + [dvG/dt]t=0,16 Dt = 0,143 + 0,2*0,08 = 0,159
m/s.
[dvG/dt]t=0,24
= 1,27 - 7,5×0,159 = 0,078 m/s².
En diminuant le pas d'itération, on peut améliorer la
résolution de l'équation différentielle par la méthode d'Euler .
Les points expérimentaux et les points calculés, conduisent à
deux courbes distinctes ( régime transitoire). L'écart entre les
valeurs reste De plus la vitesse limite est la même : en conséquence le
modèle f = -kv
est valide. inférieur à 10%.
valeur de f : d'une part f= kvG; d'autre part f= 6 ph RvG ; de plus B= k/m
d'où : k=Bm = 6 ph R soit h = Bm/(6 p R) =
7,5*35 10-3 / (6*3,14*2 10-2)=0,7. ( SAE 50)
|
|
hydrolyse
basique des esters (6,5 points)
- Cinétique de la saponification du méthanoate d'éthyle
On étudie la cinétique de la réaction d'hydrolyse basique d'un ester,
le méthanoate d'éthyle par la mesure de la conductance du mélange de
méthanoate d'éthyle et de solution d'hydroxyde de sodium NaOH (ou
soude) en fonction du temps.
Protocole expérimental :
On verse dans un becher une solution d'hydroxyde de sodium (ou soude)
de concentration C0 = 1,00.10 -2 mol.dm-3.
On plonge la cellule conductimétrique dans la solution et on met en
marche l'agitation.
On mesure la conductance initiale G0 à un instant que l'on
désigne par t0.
On ajoute alors rapidement le méthanoate d'éthyle, en quantité égale à
celle de la soude initiale.
On mesure la conductance de la solution en fonction du temps. Les
mesures sont reportées dans le tableau :
|
t (min)
|
0
|
3
|
6
|
9
|
12
|
15
|
45
|
fin
|
|
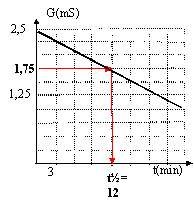
G(mS)
|
?
|
2,16
|
1,97
|
1,84
|
1,75
|
1,68
|
1,2
|
1,05
|
|
Avancement
x (mmol)
|
0
|
0,46
|
0,72
|
0,90
|
1,0
|
1,10
|
1,70
|
2,00
|
L'équation de la réaction étudiée est :HCO2 - CH2
- CH3 + HO- = HCO2- + CH3
- CH2 - OH
À un instant t la conductance du mélange est donnée par la relation :
G = k( lNa+ [Na+] + lHO- [HO-] + lHCO2-
[HCO2-] ) avec k la constante de cellule, k = S/l
= 0,01 m et l la conductivité molaire
ionique.
Les conductivités molaires ioniques de quelques ions à 25°C sont
données dans le tableau ci-dessous :
|
ion
|
Na+(aq)
|
HO-(aq)
|
HCO2- (aq)
|
|
l en S.m².mol-1
|
5,01 10-3
|
19,9 10-3
|
5,46 10-3
|
Remarques : Le volume de méthanoate d'éthyle est négligeable devant le
volume V d'hydroxyde de sodium. Le volume du mélange est égal à 200 cm3
et la concentration C0 = 1,00.10 -2 mol.dm-3.
La solution d'hydroxyde de sodium étant nettement basique on négligera
la présence des ions H3O+ devant les autres ions
du mélange réactionnel.
Soient n0 la quantité de matière initiale d'ions hydroxyde
et d'ions sodium et n0 la quantité de matière initiale de
méthanoate d'éthyle.
- On considère la solution d'hydroxyde de sodium de volume V à
l'instant t0. Donner la concentration des ions dans cette
solution à cet instant. Montrer que la conductance G0 peut
s'écrire : G0 = k n0 /V (lNa+
+ lHO- ) (1) En utilisant les
unités conventionnelles du Système International, calculer la valeur de
G0.
- On note x, l'avancement de la réaction à un instant t. Etablir le
tableau d'avancement.
- On étudie la conductance de la solution en fonction du temps. Montrer
que la conductance du mélange à un instant t en fonction des quantités
de matière initiales et de l'avancement x peut s'écrire :
Gi = S/l [ lNa+ n0
+ lHO- (n0 - x) + lHCO2- x ] (2)
- On veut montrer que la mesure de la conductance Gi permet
de connaître l'avancement x en établissant une relation simple entre Gi
et x. Simplifier l'expression (2) pour montrer qu'on peut écrire Gi
sous la forme Gi = a x + b (3), a et b étant des constantes
qui contiennent les conductivités molaires ioniques et les quantités de
matière initiales n0.
* À quelle grandeur correspond le coefficient b ? Quel est le signe de
la constante a ?
* Quelle serait l'allure de la représentation graphique Gi
en fonction de x (relation (3)) ?
- La relation (3) a permis de calculer les valeurs de l'avancement x
qui sont indiquées dans le tableau précédent. Tracer la courbe donnant
les variations de x en fonction du temps. On prendra comme échelle en
abscisse 1 cm pour 3 min et en ordonnée 1 cm pour 0,20 mmol.
- Donner la définition de la vitesse volumique de la réaction et
préciser comment on la déterminerait à un instant t.
* Comment varie la vitesse de la réaction étudiée ?
* Définir le temps de demi-réaction. Évaluer graphiquement ce temps.
- Quelques réactions de saponification
L'hydrolyse basique des esters est utilisée dans l'industrie pour
préparer des alcools à partir des substances naturelles. Elle connaît
aussi des applications dans le domaine médical mais la principale reste
toutefois la fabrication des savons. Le palmitate d'hexadécyle est le
principal constituant du blanc de baleine (cire animale). Berthelot
préparait l'alcool cétylique (hexadécanol) par saponification du blanc
de baleine. Au cours de cette réaction, il se forme aussi le palmitate
de sodium de formule CH3-(CH2)14-COONa.
Certains fils de suture utilisés en chirurgie sont des polyesters de
l'acide lactique. Leur hydrolyse dans l'organisme permet de les
résorber sans danger car l'hydrolyse redonne l'acide lactique CH3-CH(OH)-CO2H.
- Reconnaître et nommer dans chacun des composés ci-dessous les
fonctions organiques.
|
hexadécanol
|
acide lactique
|
palmitate d'hexadécyle
|
|
C15H31CH2OH
|
CH3-CH(OH)-CO2H.
|
CH3-(CH2)14-COO-(CH2)15-CH3
|
- On réalise la réaction de saponification du palmitate d'hexadécyle.
* Montrer que la réaction conduit à la formation du palmitate de sodium
: CH3-(CH2)14-COONa.
* Définir les termes hydrophile et hydrophobe. Indiquer les parties
hydrophile et hydrophobe dans la formule de l'ion CH3-(CH2)14-COO-
corrigé
[Na+]=[HO-]en
mol/m3 = Qté de matière(mol) / volume solution en m3=
n0 / V
conductivité (S m-1)
s = lNa+
[Na+] + lHO- [HO-]
conductance G0 (S) et conductivité sont
proportionnelles : G= ks
G0 = k( lNa+
[Na+] + lHO- [HO-] )
= kn0 / V(lNa++lHO-
)
k= 0,01 m; n0= 0,2 10-2 = 2 10-3
mol ; V= 2 10-4 m3.
G0 = 0,01*2 10-3/ 2 10-4(5,01+19,9)10-3
= 2,49 10-3 S = 2,49 mS.
|
HCO2 - CH2 - CH3
|
+ HO-
|
= HCO2-
|
+ CH3 - CH2 - OH
|
|
initial
|
n0
|
n0
|
0
|
0
|
|
en cours
|
n0-x
|
n0-x
|
x
|
x
|
|
fin
|
n0-xfin
|
n0-xfin
|
xfin
|
xfin
|
s = lNa+
[Na+] + lHO- [HO-]+ lHCO2- [HCO2-]
s = lNa+n0/V+
lHO-(n0-x)/V+ lHCO2-x/V
G = ks = k/V ( n0 lNa+ +lHO-(n0-x)+
lHCO2-x)
G = k/V (
n0 lNa+ +lHO-n0-lHO-x
+lHCO2-x)
G = k/V (
n0(lNa+ +lHO-)+ x( lHCO2--lHO-))
de la forme G= a+b x avec b= n0(lNa+
+lHO-)k/V = G0.
et a = lHCO2--lHO-)k/V ; a est négatif car lHO- > lHCO2-
La courbe obtenue est une droite ; la fonction affine associée
est décroissante.
vitesse volumique (mol L-1 s-1) = 1/V *
dx/dt avec V (L); x avancement (mol) et t en seconde.
La vitesse volumique diminue au cours du temps car la
concentration des réactifs diminue.
à t=t½, l'avancement est égal à la moitié de
l'avancement final soit x½= 1 mmol ( lecture tableau)
alors G½= 1,75 mS ; le graphe donne t½ =
12 min.
|
hexadécanol
|
acide lactique
|
palmitate d'hexadécyle
|
|
|
CH3-(CH2)14-COO-(CH2)15-CH3
|
C15H31CH2OH
alcool primaire
CH3-CH(OH)-CO2H.alcool
secondaire
CH3-CH(OH)-CO2H acide carboxylique
CH3-(CH2)14-COO-(CH2)15-CH3
ester
CH3-(CH2)14-COO-(CH2)15-CH3
+ Na+ + HO---> CH3-(CH2)14-COO-
+ Na+ + HO(CH2)15-CH3
-----------------COO-
partie hydrophobe ..........tête hydrophile
la longue chaîne carbonée CH3-(CH2)14
constitue la partie hydrophobe ou lipophile( amie des graisses,
lipides, enemie de l'eau, qui fuit l'eau)
le groupe -COO- constitue la partie hydrophile,
amie de l'eau, qui est attiré par l'eau.
|
|
diapason
électronique( 4 points)
Un groupe d'élèves musiciens souhaite réaliser un diapason
électronique capable d'émettre des sons purs, en particulier la note la3
(note la du troisième octave). Cette note sert de référence aux
musiciens pour accorder leurs instruments. Un son pur est une onde
acoustique sinusoïdale de fréquence donnée. Il peut être obtenu par
excitation d'un haut-parleur à l'aide d'une tension électrique
sinusoïdale de même fréquence.
Le circuit électrique qui permet d'obtenir une tension
sinusoïdale est constitué d'une bobine, d'un condensateur et d'une
résistance
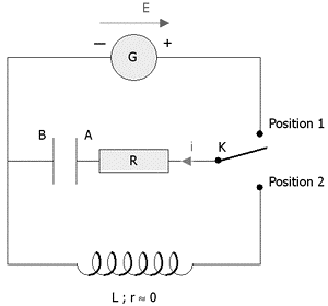
|
E= 12 V ; G générateur de tension constante
R= 1000 W.
C= 1 m F
L inductance réglable et r négligeable
|
Les élèves vont réaliser les différentes étapes du circuit oscillant
permettant d'émettre les sons de la gamme tempérée (gamme musicale
élaborée par J.S. Bach et couramment utilisée en Occident). Ils
étudieront :
· dans un premier temps, la charge du condensateur.
· dans un deuxième temps, l'établissement des oscillations
électriques.
· dans un troisième temps, l'influence des paramètres du
circuit leur permettant d'obtenir la note souhaitée.
|
note
|
do
|
ré
|
mi
|
fa
|
sol
|
la
|
si
|
|
fréquence (Hz)
|
262
|
294
|
330
|
349
|
392
|
440
|
494
|
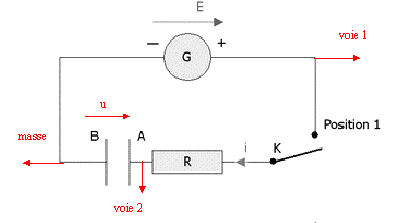
- Charge du condensateur :Le condensateur étant initialement
déchargé, l'interrupteur K est basculé en position 1, à l'instant t =
0. Le sens positif de circulation du courant est indiqué sur le schéma.
On visualise la charge du condensateur, à l'aide d'un oscilloscope à
mémoire.
- Représenter, sur le schéma, la tension u aux bornes du condensateur
par une flèche correctement orientée, en respectant la convention
récepteur.
-Ajouter, sur le schéma précédent, les connexions à l'oscilloscope
permettant de visualiser à la fois : sur la voie 1 : la tension E
positive, aux bornes du générateur. sur la voie 2 : la tension u, en
convention récepteur, aux bornes du condensateur.
- Soient A et B, les armatures du condensateur. Donner la relation
entre la charge qA de l'armature A, l'intensité i et le
temps t.
- Donner la relation entre la charge qA , la tension u et la
capacité C.
- En vous aidant des réponses aux questions précédentes et en
appliquant la loi d'additivité des tensions, établir l'équation
différentielle régissant l'évolution de la tension u aux bornes du
condensateur, lors de sa charge.
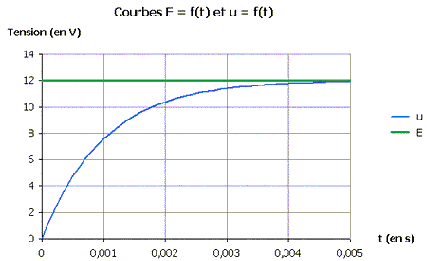
Vérifier que la solution suivante u= E(1-exp(-t/(RC)) est solution de
l'équation différentielle établie précédemment.
- Constante de temps t. Rappeler
l'expression de la constante de temps t de
ce circuit, en fonction de R et de C.
* Vérifier que la constante t est homogène
à une durée, en utilisant l'équation différentielle précédemment
établie ou sa solution.
* Déterminer graphiquement la valeur de t,
en justifiant la méthode employée.
* Au bout de combien de temps, exprimé en fonction de t , considère-t-on le condensateur totalement
chargé ?
- Réalisation d'oscillations électriques : Le condensateur C
est à présent chargé sous la tension E du générateur ; on bascule
l'interrupteur K en position 2. Cet instant est choisi comme nouvelle
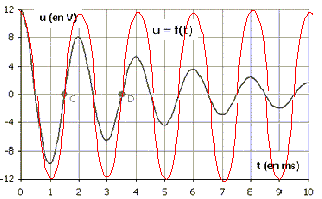
origine des temps. La tension u aux bornes du condensateur évolue en
fonction du temps de la manière suivante.
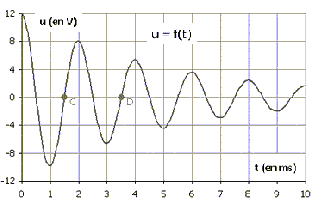
- Les oscillations électriques observées sont amorties.
Quel est le dipôle responsable de cet amortissement ? Qualifier ce
régime d'oscillations par un terme approprié.
-Sur la courbe u = f(t) présentée, sont notés deux points C et D.
Comment appelle-t-on la durée écoulée entre ces deux points ? Évaluer
graphiquement cette valeur.
-Les élèves pensent que le circuit ainsi réalisé n'est pas utilisable.
Indiquer la raison qui leur permet de faire cette constatation.
- Entretien des oscillations :En feuilletant leur manuel de
physique, les élèves constatent qu'il est possible de rajouter au
circuit précédent, un dispositif qui entretient les oscillations.
Expliquer, en une phrase, le rôle de ce dispositif, d'un point de vue
énergétique.
- Sachant que les paramètres du circuit précédent n'ont pas été
modifiés, représenter,, la courbe u = f(t) obtenue après entretien des
oscillations.
- Rappeler l'expression de la période propre T0 du circuit
oscillant. Calculer sa valeur, sachant que le condensateur a une
capacité C = 1,0 µF et que l'inductance L de la bobine vaut ici 0,100 H.
- En déduire la fréquence f0 de la tension obtenue.
-Le circuit oscillant est relié à un haut-parleur convertissant cette
onde électrique en onde sonore de fréquence f0. Les élèves souhaitent
accorder leurs instruments en émettant la note la3 à l'aide
du circuit précédent. La fréquence précédemment obtenue est-elle un son
de l'octave 3 de la gamme ?
* Quels paramètres peut-on changer pour modifier la valeur de la
fréquence émise ?
* Sachant que les élèves ne disposent pas d'autre condensateur que
celui du circuit initial, calculer la valeur de l'autre paramètre qui
permettra d'obtenir la note la3 .
* On règle à présent ce paramètre sur 232 mH ; déterminer la nature de
la note alors émise par le diapason.
corrigé
dqA/dt = i ; qA= C u soit i= Cdu/dt = C
u'
u+Ri = E ; u + RC u'= E (1)
u= E(1-exp(-t/(RC)) ; dériver par rapport au temps u'= E/(RC)
exp(-t/(RC)
repport dans (1) : E-E
exp(-t/(RC)) + RC E/ (RC) exp(-t/(RC) = E toujours vérifier quel
que soit t
en conséquence la fonction u= E(1-exp(-t/(RC)) est solution de
l'équation différentielle (1).
constante de temps t= RC ;
l'expression (-t/(RC), contenue dans l'exponentielle doit être sans
dimension; en conséquence RC a la dimension d'un temps.
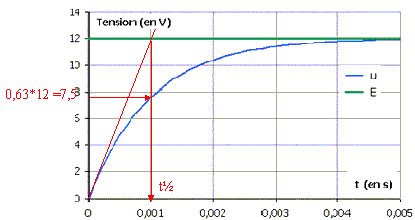
t voisin 10-3 s.
La charge du condensateur est terminée au delà de t= 5t
Le résistor est
responsable de l'amortissement. Le régime est pseudo-périodique
La durée écoulée entre les points C et D est une période T = 2
10-3 s ( lecture graphe entre 2 maxima suxccessifs)
Le circuit ainsi réalisé n'est pas utilisable du fait de
l'amortissement : période T proche de T0( régime périodique)
et diminution de l'amplitude.
entretenir les oscillations, c'est compenser à chaque instant,
l'énergie perdue par effet joule dans le résistor.
T0= 2p(LC)½=
6,28 ( 10-6*0,1)½=1,99 10-3
s.
fréquence, inverse de la période exprimée en seconde : f0
=1/1,99 10-3= 503,5 Hz.
La fréquence du la3 est 440 Hz : le son obtenu
n'est pas celui du la3.
On modifie la valeur de l'inductance L de la bobine :
nouvelle période T= 1/440 s; T²= 4p²
LC soit L= T²/( 4p² C)=1/(4402*4*3,142*10-6)=
0,131 H.
si L= 0,232 H alors la période vaut : 2*3,14*(0,232 10-6)½=
0,003 s
fréquence : 330 Hz (mi) .
|
|
retour -menu
|