La radioactivité En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
		. .
	. .
	noyau d'un atome: ZA X X : symbole de l'élément chimique Z est le nombre de protons. Z nombre de charge. A est le nombre de nucléons. A nombre de masse. N = A - Z est le nombre de neutrons présents dans le noyau. isotopes : même nombre de charge mais des nombres de nucléons A différents. lois de conservation : lors d'une désintégration radioactive a ou b il y a conservation du nombre de charge Z et du nombre de nucléons A. radioactivité a ZAX-->Z-2A-4Y+24He radioactivité b- ZAX-->Z+1AY+-10e radioactivité b+ ZAX-->Z-1AY++10e désexcitation g : un nouyau exité libère l'énergie excédentaire en émettant un photon g. 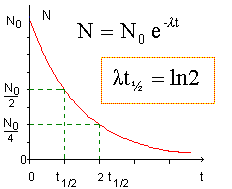loi de décroissance radioactive   demi-vie radioactive,(ou période) notée t½ : durée au bout de laquelle la moitié des noyaux radioactifs initiaux se sont désintègrés. L'activité A : nombre moyen de désintégrations par seconde Elle s'exprime en becquerels dont le symbole est Bq (1Bq=1 désintégration par seconde). A = lN la masse est une des formes que peut prendre l'énergie E = m.c2 E: énergie du système en joules (J) ; m: masse du système en kilogrammes (kg) ; c: vitesse de la lumière dans le vide (c=3,0.108m.s-1) La fusion nucléaire est une réaction au cours de laquelle deux noyaux légers s'unissent pour former un noyau plus lourd. La fission est une réaction nucléaire provoquée au cours de laquelle un noyau lourd "fissible" donne naissance à deux noyaux plus légers	L'uranium 238 (Z=92) est radioactif a. Le noyau fils obtenu est radioactif b -, etc... A partir de l'uranium 238, et après x désintégrations a et y désintégrations b - le noyau stable obtenu est le plomb 206 ( Z=82). - Quelles sont les valeurs de x et y ? Une substance radioactive, dont la demi-vie vaut 15 s émet initialement 3 108 particules a par seconde. Combient reste-t-il de noyaux radioactifs après 45 s ? La mesure de la radioactivité du carbone 14 dans les bois carbonisés lors d'une éruption volcanique donne en moyenne 4,8 désintégrations par gramme et par minute (d.p.m) alors qu'un bois vivant donne 13,5 d.p.m en moyenne. La demi-vie du carbone 14 vaut 5590 ans. - A quelle époque remonte l'éruption volcanique ? corrigé 23892U--> 23490X + 42He lors d'une émission alpha : le nombre de masse diminue de 4 et le numéro atomique diminue de 2. 23490X --> 23491Y + 0-1e lors d'une émission béta : le nombre de masse ne change pas et le numéro atomique augmente de 1. en passant de 23892U au plomb 20682Pb il faut x désintégrations alpha et y désintégrations béte. 238-206 = 32 = 4x soit x=8 92-82=10 = 2x -y soit y = 6 45 s = 3 demi-vie radioactive : l'activité est en conséquence divisée par 23 = 8 A0 = 3 108 Bq et A(t=45s) = 3/8 108=3,75 107 Bq constante radioactive : l= ln2 / t½ = 0,046 s-1. A0=lN0 soit N0 = 3 108 / 0,046 = 6,52 109 noyaux initiaux N= N0/8 = 8,15 108 noyaux à la date t=45 s. A =A0 exp(-lt) soit ln (A0/A)=lt avec lt½=ln2 ln (A0/A)= ln2 t / t½ soit t = t½ ln (A0/A)/ ln2 t = 5590*ln(13,5/4,8)/ 0,693 = 8340 ans.
	. .
	Le radium 22688Ra se désintègre spontanément en émettant une particule a. Le noyau fils est un isotope du radon (Rn), gaz dans les conditions ordinaires de température et de pression. L'isotope 22688Ra est radioactif b-. Préciser en le justifiant si la masse d'un noyau de radium est égale à la somme des masses de ses nucléons. Ecrire l'équation de désintégration du radium 22688Ra. Préciser en le justifiant si le radium 22688Ra et le radon 22686Rn sont isotopes. Donner le nom du noyau fils résultant de la désintégration du radium 22688Ra. La demi vie du radon 22286Rn est de 3,8 jours. Donner le pourcentage de noyaux de radon 22286Rn restants par rapport au nombre initial au bout de 11,4 jours. Le noyau de radium 22688Ra est obtenu à partir d'une suite de désintégrations radioactives a et b- du noyau d'uranium 23892U. Déterminer le nombre de particules a et le nombre d'électrons émis au cours de ces désintégrations successives. Un échantillon de "radium 226" a un activité de 6 105 Bq. Déterminer le nombre de noyaux de radium 22688Ra désintégrés en une minute. Déterminer l'énergie libérée ( en MeV) au cours de de la réaction de désintégration du radium 22688Ra. La teneur en radon 22286Rn dans les gaz du sol a été déterminée en mesurant une activité de 3,75 103 Bq par m3 de gaz prélevé. La constante radioactive l du radon est 2,1 10-6 s-1. déterminer la quantité de matière (mol) en 22286Rn dans 1 m3 responsable de cette activité. NA= 6,02 1023 mol-1.masse noyau helium : 4,003 u ; masse du noyau de radium 226 : 226,05 u ; masse du noyau de radon 222 : 222,042 u; énergie de masse correspondante à 1u : 930 MeV Radon (Z=86) ; Francium (Z=87) ; Radium (Z=88) : Actinium (Z=89) ; Thorium (Z=90) ; Proactinium (Z=91) ; Uranium (Z=92) aide aux calculs : 3,75 / 2,1 = 1,79 ; 1,79 / 6,02 = 0,3.   corrigé la masse d'un noyau de radium est inférieure à la somme des masses de ses nucléons : la perte de masse correspond à l'énergie de cohésion du noyau 22688Ra-->22286Rn + 42He ( noyau fil "radon 222" ) deux isotopes ne diffèrent que par leur nombre de neutrons ( donc même numéro atomique ) : le radium 22688Ra et le radon 22686Rn ne sont donc pas isotopes. 11,4 jours correspond à 3 fois la demi vie : donc le nombre de noyaux initiaux est divisé par 23 = 8 ; il ne reste donc que 12,5 % de noyaux radioactifs. à chaque désintégration b- le numéro atomique augnente de 1 unité alors que le nombre de masse A ne change pas. à chaque désintégration a le numéro atomique diminue de 2 unités et le nombre de masse diminue de 4 unités or le nombre de masse diminue de 238-226 = 12 unités : donc 3 désintégrations de type a. en conséquence le numéro atomique diminue de 6 unités ; or au total on observe une diminution de 92-88 = 4 unités donc 2 désintégrations de type b-. l'activité est le nombre de désintégrations par seconde soit 6 105. en 1 min = 60 secondes : 60*6 105 = 3,6 107 noyaux se désintègrent. |Dm|= |4,003 + 222,042-226,05| =5 10-3 u énergie libérée : 5 10-3*930 = 4,65 MeV. A=l N soit N= A /l = 3,75 103 / 2,1 10-6 = 3,75/2,1 109 = 1,79 109 noyaux dans une mole il y a 6,02 1023 noyaux Quantité de matière (mol) = 1,79 109 / 6,02 1023 = 1,79 /2,1 10-14 = 0,3 10-14 mol.
	Première partie : fission de l’uranium ( Geipi 2004) Parmi les réactions, très variées, de fission de l’atome d’uranium 235 bombardé par des neutrons lents, on considère la réaction suivante : 235 92U + 01n--> 139 xXe +94 38Sr + y01n Compléter l’équation en calculant x et y. À partir du tableau placé à la fin de l’énoncé, calculer : a) l’énergie E, en joules puis en MeV, libérée par la fission d’un noyau d’uranium 235, b) l’énergie E', en joules, libérée par la fission d’une masse M = 1 kg d’uranium 235. Deuxième partie : Fusion de l’hydrogène L’hydrogène possède trois isotopes stables11H, 21H et 31H, - Ecrire les différentes réactions qui, à partir de deux noyaux d’isotopes identiques ou différents, conduisent à la formation d’un noyau d’hélium accompagné ou non d’une ou plusieurs particules - Parmi ces possibilités, on s’intéresse à celle qui produit un neutron en plus du noyau d’hélium. A partir des données de l’énoncé : a) encadrer la réaction correspondante parmi celles écrites dans le document réponse b) calculer l’énergie E, en joules, accompagnant la production d’un noyau d’hélium, c) calculer l’énergie E' libérée par la fusion totale d’une masse M = 1 kg de mélange contenant le même nombre d’atomes des deux isotopes. Troisième partie : comparaison des deux procédés Cocher dans le tableau du document réponse, les cases correspondantes aux réponses qui vous semble correctes. fission fusion Plus grande abondance des réserves de combustible Production moindre de déchets radioactifs Pas de risque d’emballement des réactions Technologie utilisée en production industrielle Données : 1 u = 1,67 10-27 kg, c = 3 108 m.s-1, e = 1,6 10-19 C. On néglige la masse des électrons. noyau ou particule 23592U 139xXe 9438Sr 10n 21H 31H 42He masse (u) 235,044 138,918 93,915 1,009 2,013 3,015 4,001 corrigé 235 92U + 01n--> 139 xXe +94 38Sr + y01n conservation de la charge : 92 = x+38 soit x= 54 conservation du nombre de nucléons : 235 +1= 139+94+y soit y = 3. diminution de masse |Dm|=235,044-(138,918+93,915+2*1,009)=0,193 u = 0,193*1,67 10-27 = 3,223 10-28 kg. énergie libérée E= |Dm| c² = 3,223 10-28 * (3 108)²=2,9 10-11 J=2,9 10-11 / 1,6 10-19 = 1,81 108 eV= 181 MeV. énergie libérée pour 1 kg d'uranium 235 : 235,044*1,67 10-27 = 3,92 10-25 kg 1 / 3,92 10-25 = 2,55 1024 réactions de fission E' = 2,55 1024 * 2,9 10-11 = 7,4 1013 J. 21H + 21H -->42He 11H + 31H -->42He 21H + 31H -->42He + 10n 31H + 31H -->42He +2 10n diminution de masse |Dm|=2,013+3,015-(4,001+1,009)=0,018 u = 0,018*1,67 10-27 = 3 10-29 kg. énergie libérée E= |Dm| c² = 3 10-29 * (3 108)²=2,7 10-12 J énergie libérée pour 1 kg des deux isotopes : (2,013+3,015)*1,67 10-27 = 8,4 10-27 kg 1 / 8,4 10-27 = 1,19 1026 réactions de fusion E' = 1,19 1026 * 2,7 10-12 = 3,2 1014 J. fission fusion Plus grande abondance des réserves de combustible x Production moindre de déchets radioactifs x Pas de risque d’emballement des réactions x Technologie utilisée en production industrielle x
	Le radon 22286Rn fait partie d’une famille radioactive qui, par une série d’émissions ß- et a, aboutit au plomb 20682Pb Ecrire l’équation de la réaction nucléaire représentant l’émission a par des noyaux AZX. Ecrire l’équation de la réaction nucléaire représentant l’émission ß- par des noyaux AZX. En déduire le nombre de désintégrations ß- et a émises pour passer du 22286Rn au 20682Pb. On prépare un échantillon de 1 mg de 22286Rn et on mesure la décroissance dans le temps de la masse m du radon restant : t(jours) 0 1 2 3 4 5 m(mg) 1 0,83 0,69 0,58 0,48 0,4 - A l’aide des données du tableau, donner l’ordre de grandeur de la demi-vie du radon 222. - Tracer le graphe de ln (m) = f(t). Indiquer la nature de la courbe obtenue. En déduire la constante radioactive l du radon 222 puis sa demi-vie. Calculer l’activité A0 de l’échantillon de radon à t = 0. Calculer la masse m10 et l’activité A10 de l’échantillon de radon à t = 10 jours. Données : Masse molaire du radon 222 : M = 222 g.mol-1 Nombre d’Avogadro : NA = 6,02 10 23 mol-1 corrigé AZX= 42He + A-4Z-2Y : émission a AZX= 0-1e + AZ+1Y : émission ß- 22286Rn fait partie d’une famille radioactive qui, par une série d’émissions ß- et a, aboutit au plomb 20682Pb : le nombre de nucléons diminue de 222-206 = 16 : donc 4 désintégrations de type a le nombre de charge diminue globalement de 4 : donc 4 désintégrations de type ß-. demi-vie : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés ; la masse initiale du radon est alors divisée par 2. D'après les données du tableau, l’ordre de grandeur de la demi-vie du radon 222 est un peu inférieure à 4 jours. 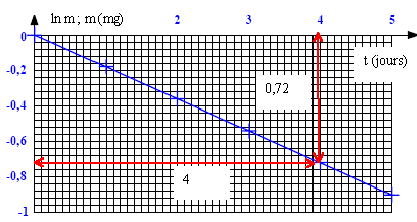coefficient directeur = -0,72 / 4 = -0,18 jour-1.
	Les trois parties sont indépendantes I. Dans les étoiles dont la masse est supérieure à 1,5 fois la masse du soleil le principal processus de fusion à l'origine de l'énergie libérée est le cycle CNO : 126C + 11H-->137N (1) ; 137N -->13ZX+ 01e (2) ; 13ZX+ 11H-->147N (3) 147N + 11H-->158O (4) ;158O -->A'Z'Y+ 01e (5) ; AZY+ 11H-->126C + 42He (6) Déterminer les valeurs de A, Z et Z' et identifier X et Y. Nommer les particules 11H et 01e Attribuer aux réactions (1) et (3) un type de réactions nucléaires. II. Energie de masse : On considère les deux réactions nucléaires suivantes : 73Li + 42He -->105B + 10n (a) ; 73Li + 42He -->115B (b) Montrer qu'une seule de ces réactions libère de l'énergie. Définir l'énergie de liaison du noyau. Poser le calcul, sans l'effectuer, permettant d'obtenir en MeV, l'énergie de liaison du noyau 115B à partir des données. On donne les valeurs des énergies de liaison de deux noyaux : 42He : 28,45 meV ; 105B : 65,12 MeV Quel est le noyau le plus stable ? Justifier. m(He) = 4,0015 u ; m(Li 7) = 7,0144 u ; m(B 10) = 10,0102 u ; m(B 11) = 11,0066 u ; m(neutron)= mn = 1,0087 u ; m(proton) = mp=1,0073 u. 1 u = 1,66054 10-27 kg ; 1 eV= 1,602 10-19 J. III. Radioactivité artificielle : On bombarde des noyaux d'aluminium 27 par des particules a pour former l'isotope 30 du phosphore. Ecrire l'équation de la réaction nucléaire de formation du phosphore 30. L'aluminium 27 n'est pas radioactif alors que le phosphore 30 est radioactif b+. Ecrire l'équation de la désintégration du phosphore 30. On arrête le bombardement des noyaux d'aluminium par les particules a : à cette date , l'échantillon de phosphore a une activité A0= 7,2 1013 Bq. On attend un peu pour que l'activité de l'échantillon devienne A= 9 1012 Bq. Quelle est la durée écoulée depuis la fin du bombardement ? Demi vie du phoshore 30 : t½=156 s. 11Na ; 12Mg ; 13Al ; 14Si ; 15P ; 16S ; 17Cl ; 18Ar ; corrigé 13ZX + 11H-->147N + (3) conservation de la charge : Z+1= 7 soit Z= 6 , X est l'élément carbone. 158O -->A'Z'Y+ 01e (5) conservation du nombre de nucléons : 15 = A' conservation de la charge : Z'+1= 8 soit Z= 7 , X est l'élément azote 11H : proton, noyau d'hydrogène ; 01e : positon (1) fusion de petits noyaux ; (2) radioactivité de type b+. variation de masse (a) : Dm= m(B 10) + mn-m(Li 7)-m(Helium 4)= 10,0102+1,0087-7,0144-4,0015 = 3 10-3 u (b) : Dm= m(B 11) -m(Helium 4)--m(Li 7) =11,0066-4,0015-7,0144 = -6,3 10-3 u réaction (b) : à une diminution (perte) de masse correspond une libération d'énergie on appelle énergie de liaison notée El d'un noyau l'énergie que doit fournir le milieu extérieur pour séparer ce noyau au repos en ses nucléons libres au repos. 115O : 5 protons et 6 neutrons Dm = 5 mp+6mn-m(B 11) exprimée en u multiplier par 1,66054 10-27 pour esprimer Dm en kg. E= Dmc² , énergie en J et c= 3 108 m/s. diviser par 1,6 10-19 pour obtenir l'énergie en eV diviser par 106 pour obtenir l'énergie en MeV. L'énergie de liaison par nucléon d'un noyau est le quotient de son énergie de liaison par le nombre de ses nucléons: plus elle est élevée plus le noyau est stable. 42He : 28,45 / 4 = 7,1 MeV/nucléons ; 105B : 65,12 / 11 = 6,51 MeV/nucléons. 2713Al + 42He -->3015P+ 10n. 3015P -->3014Si + 01e. loi de décrioissance radioactive : A(t) = A(0) exp(-lt) A(0) /A(t) = 7,2 1013 / 9 1012 = 8 = 23. l'activité diminue de moitié au bout d'une demi-vie ; est divisée par 4 au bout de 2 demi-vie et est divisée par 8 au bout de 3 demi-vie. t= 3*156 = 468 s.
	retour -menu