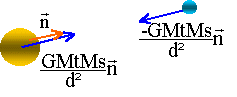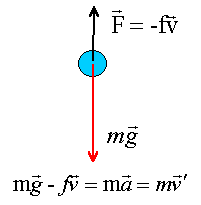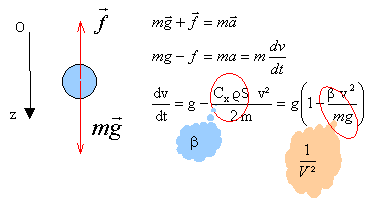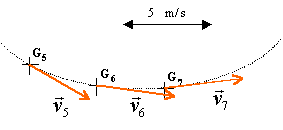
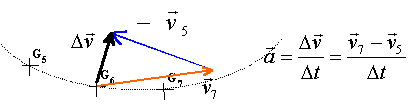
référentiel :

Un référentiel est un solide par rapport auquel on étudie un mouvement On prend souvent comme référentiel le solide Terre.

- Le référentiel géocentrique (construit à partir des centres de la Terre et de trois étoiles lointaines qui paraissent fixes) est utilisé pour étudier le mouvement des satellites terrestres.

- Le référentiel héliocentrique ( construit à partir des centres du soleil et de trois autres étoiles, ) est utilisé pour étudier les voyages interplanétaires ou le mouvement des planètes autour du Soleil.

Un repère d'espace orthonormé, lié à un référentiel, est un système d'axes orthogonaux et normés, muni d'une origine O. Dans ce repère, on peut exprimer les coordonnées du mobile ponctuel étudié.

La trajectoire d'un mobile ponctuel est constituée par l'ensemble des positions successives occupées par le mobile au cours du temps.

vitesse moyenne (m/s) = distance parcourue (m) / durée du parcours (s)

vecteur vitesse instantanée = dérivée du vecteur position par rapport au temps.

ce vecteur est porté par la tangente à la trajectoire à la date considérée et a toujours le sens du mouvement.

La vitesse s'exprime en m / s dans le système international d'unités 1 m / s = 3,6 km / h.

Dans un référentiel donné le vecteur vitesse d'un mobile ponctuel peut changer de valeur et (ou) de direction. Ce changement éventuel peut se faire plus ou moins rapidement. On appelle vecteur accélération instantanée du mobile ponctuel la dérivée par rapport au temps du vecteur vitesse.

Le vecteur accélération est dirigée vers l'intérieur de la trajectoire ; l'accélération s'exprime en m / s² dans le système international d'unités.

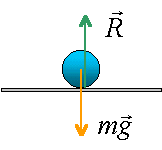
Un référentiel galiléen est un référentiel dans lequel le principe de l’inertie est vérifié.

Dans un référentiel galiléen, si la somme vectorielle des forces extérieures appliquées à un solide est nulle ( solide pseudo-isolé ) alors le centre d’inertie G de ce solide est soit au repos, soit animé d'un mouvement rectiligne uniforme et réciproquement.

Un solide peut donc se déplacer même si la somme des forces appliquées à ce solide soit nulle. La véritable opposition n'est pas entre mouvement et repos mais entre mouvement rectiligne uniforme (le repos n'est qu'un simple cas particulier) et les autres types de mouvement.

Dans un référentiel galiléen, si le vecteur vitesse du centre d'inertie d'un solide varie, alors la somme vectorielle des forces extérieures appliquées à ce solide n'est pas nulle et réciproquement. La direction et le sens de cette somme sont ceux de la variation du vecteur vitesse entre deux instants proches.

Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération de son centre d'inertie.

vitesse	variation du vecteur vitesse

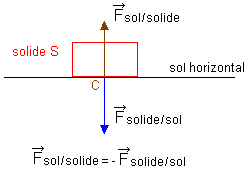
Interaction entre un objet A et un objet B : si un solide noté A exerce sur un solide noté B une force notée F _{A / B}, alors B exerce sur A une force notée F _{B / A} . Les deux forces associées à une même interaction sont toujours égales et opposées.

action du support	force gravitation entre terre et lune

un vecteur est écrit en gras et en bleu.

En un point donné M, au voisinage de la Terre, le poids d'un objet de masse m peut s'écrire : P = mg

g : vecteur champ de pesanteur terrestre au point M considéré, direction la verticale passant par M, sens :de haut en bas.

La valeur de l'intensité g de la pesanteur dépend de la latitude du point M où l'on se trouve ( 9,78 N / kg à l'équateur,

g = 9,83 N / kg au pôle Nord, au niveau de la mer) et de son altitude (diminution d'environ 1 % à l'altitude de 30 km).

Dans un domaine au voisinage de la Terre (dimensions de l'ordre de quelques kilomètres), on peut considérer que le champ de pesanteur est uniforme : le vecteur champ de pesanteur a même direction, même sens et même valeur en tout point de ce domaine restreint .

est une force de contact répartie sur la surface de contact solide-fluide. On la représente par un vecteur :

origine : le centre d'inertie C du volume de fluide déplacé.

direction : la verticale passant par C

sens : du bas vers le haut

valeur : P = r_fluideVg égale au poids du fluide déplacé.

r_fluide : masse volumique du fluide (kg/m³) ; V volume fluide déplacé (m³)

Si un solide se déplace dans un fluide, il apparaît des forces de "frottement fluide" sur toute la surface du solide.

Ces forces de frottement fluide peuvent être résistantes (chute d'une bille ralentie par la présence d'air ou d'eau) ou motrices (feuille emportée par le vent). On les modélise par un vecteur f de sens opposé au mouvement si les frottements sont résistants.

La valeur de la force de frottement sera modélisée par une expression de la forme :

f = k.V pour les vitesses faibles ou f = k.V ² pour des vitesses plus importantes.

Un solide est en chute libre s'il n'est soumis qu'à son poids.

On considère un axe vertical orienté vers le haut dont l'origine est le sol.

vitesse : v = -g t + v₀ ( v₀ : vitesse initiale m/s)

distance parcourue : d = - ½gt² + v₀t + d₀ avec d₀ altitude initiale(m)

f proportionnelle à la vitesse	f proportionnelle à la vitesse au carré