dipôle RLC En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
		. .
	. .
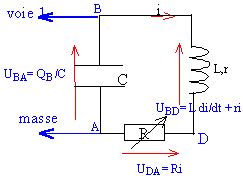
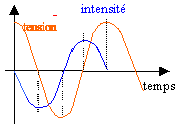
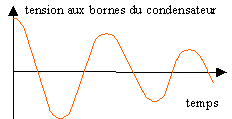
	LCu" + (R+r)C u' + u = 0. équation différentielle du circuit. si les résistances sont négligeables : LCu" + u = 0 soit u" + 1/(LC) u = 0 on pose w0² = 1/ (LC) ; w0 : pulsation en rad /s. tension aux bornes du condensateur échange d'énergie entre bobine et condensateur. régime pseudopériodique ( r croît) régime apériodique (r grand)	La tension aux bornes d'un condensateur AB de capacité C=0,1 mF est U0=10 V. Déterminer la charge q0 stockée dans ce condensateur. A la date t0 ce condensateur est branché aux bornes d'une bobine de résistance négligeable et d'inductance L= 1 H. L'intensité du courant est nulle à cet instant. - Faire le schéma du montage et établir l'équation différentielle à laquelle satisfait la charge q(t) du condensateur. - Calculer la pulsation propre w0 ainsi que la période propre T0. - En utilisant les conditions initiales donner l'expression de la charge q(t) du condensateur en fonction de t, w0 C et U0 ainsi que l'expression de l'intensité i(t) en fonction de t, w0 C et U0. - En déduire l'expression de la tension UAB(t) aux bornes du condensateur en fonction de t, w0 et U0 - On visualise UAB(t) sur l'écran d'un oscilloscope ( 0,5 ms/div et 5 V/div). Représenter la courbe observée sur l'écran de 8 cm de large. Donner l'état du condensateur (charge, tension aux bornes, énergie stockée) ainsi que l'intensité du courant et l'énergie WL de la bobine aux dates t=0 ; t1=0,25 T0 ; t2=0,5 T0 ; t3=0,75 T0 . Données : racine carrée 10-7 = 3,2 10-4 ; racine carrée(107 )= 3200 ; 2p racine carrée 107 = 2 10-3 ; corrigé charge q0 = CU0 = 10-7*10 = 10-6 C. 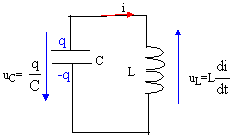q/C + Ldi/dt = 0 avec i= dq/dt soit di/dt = d²q/dt² = q" q/C+Lq"=0 ou bien q" + 1/(LC)q=0 on pose w²0= 1/(LC) d'où T0= 2p/ w0 = 2p (LC)½ . w0 = 1/(LC)½ =1/(1*10-7)½= 3200 rad/s. période T0= 2*3,14 / 3200 = 2 10-3s. les solutions de l'équation différentielle sont de la forme q(t) = QM cos(w0 t+j) à l'instant initial, le condensateur est chargé : QM= CU0. QM= QMcos(j) donne j =0 q(t) = CU0 cos(w0 t). dériver par rapport au temps pour obtenir l'intensité i = CU0 (-w0 ) sin(w0 t) tension aux bornes du condensateur : u(t)= q(t) / C = U0 cos(w0 t). 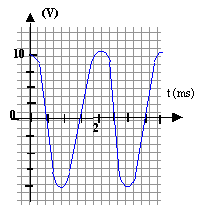8 cm de large correspondent à 8*0,5 = 4 ms soit deux périodes. temps (ms) 0 0,5 1 1,5 charge (C) 10-6 0 -10-6 0 tension aux bornes du condensateur(V) 10 0 -10 0 énergie stockée ( condensateur) ½CU² 5 mJ 0 5 mJ 0 intensité (mA) 0 CU0 (-w0 ) = -3,2 0 3,2 énergie stockée dans la bobine ½Li² 0 5 mJ 0 5 mJ
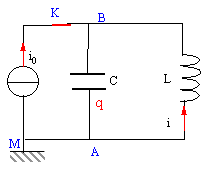
	Un générateur de courant constant délivre un courant d'intensité i0 = 200 mA en étant connectées à l'ensemble d'une bobine et d'un condensateur reliés en parallèle (voir schéma). La bobine dont le coefficient d'inductance vaut L = 200 mH possède une résistance nulle. La capacité du condensateur est C= 200 nF. A l'instant t = 0 considéré comme origine des temps, on ouvre l'interrupteur K. Que valent pour t = 0(juste avant l'ouverture de l'interrupteur K) l'intensité dans la bobine ? Justifier. - la tension aux bornes du condensateur ? Justifier. On ouvre l'interrupteur K. Etablir l'équation différentielle du circuit à laquelle obéit la charge q(t) = q de l'armature du condensateur relié à A. On fera obligatoirement un schéma faisant apparaître les tensions utilisées. - En déduire l'équation différentielle à laquelle obéit la tension u = uAB. -Cette dernière équation différentielle a une solution de la forme u= Asin (w0t + j ). En tenant compte des conditions pour t = 0 déterminer d'une part A en fonction de i0, C et w0 d'autre part j de façon que A soit une valeur positive. Donner sans démonstration l'expression littérale de w0 en fonction des caractéristiques du circuit. Calculer : - la période du phénomène. - la tension maximum um - exprimer l'intensité i en fonction du temps. Calculer l'énergie initiale stockée dans la bobine. - par des considérations énergétiques recalculer la valeur de um.   corrigé K fermé : l'intensité du courant i0 est constante ; sa dérivée par rapport au temps est nulle en conséquence la tension aux bornes de la bobine u=Ldi0/dt est nulle. bobine et condensateur sont en dérivation, donc la tension aux bornes du condensateur est nulle et le condensateur ne se charge pas. Par contre la bobine stocke l'énergie ½Li0² =0,5*0,2*0,2² = 4 10-3 J. donc à t=0 : intensité dans la bobine : i0 tension aux bornes du condensateur uAB=0. 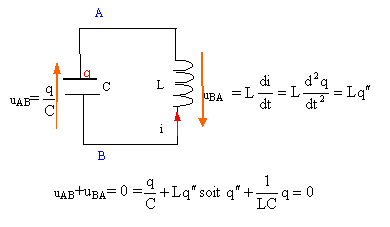charge q et tension aux bornes du condensateur sont proportionnelles : q=Cu d'où u"+ 1/(LC) u=0. on pose w0²= 1/(LC) = 1/(0,2*20010-9)= 108/4 soit w0= 5000 rad/s période T= 2 p/ w0= 2*3,14/5000 =1,256 ms. à t =0 la tension aux bornes du condensateur est nulle : u(0) = 0 = A sin j soit j = 0 ou j=p. charge q(t) = Cu(t) = CA sin (w0t + j ). dériver par rapport au temps pour obtenir l'intensité : i = CAw0cos (w0t + j ). à t=0 l'intensité vaut i0 dans la bobine : i0 = CAw0cos ( j ). i0, CAw0étant positifs on élimine la valeur j=p. A= i0 /( Cw0)= umax = 0,2/(200 10-9 *5000)=1000*0,2 = 200 V. i(t) =0,2 cos(w0t ) énergie initialement stockée dans la bobine : ½Li0² =0,5*0,2*0,2² = 4 10-3 J. échange permanent d'énergie entre bobine et condensateur : le condensateur stocke au plu s : 4 10-3 = ½Cu²max soit u²max= 8 10-3 /C = 8 10-3 / 2 10-7 =4 104 ; umax = 200 V.
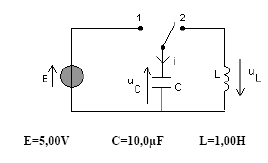
	On néglige la résistance interne de la bobine. Initialement l’interrupteur est en position 1 depuis un temps très long. A t = 0, on bascule l’interrupteur de la position 1 vers la position 2. Dans tout l’exercice, on considérera que l’interrupteur a déjà basculé. Exprimer uc en fonction de uL. - Exprimer i en fonction de uc. - Exprimer uL en fonction de i. En déduire l’équation différentielle à laquelle obéit uc. La solution de l’équation précédente est de la forme : uc= U0 cos ( 2pf t+j), U0 et j sont des constantes. - Donner l’expression littérale et la valeur numérique de f. Quelle est l’unité de f ? - Donner l’expression littérale du courant i en fonction du temps. - Indiquer les valeurs de uc (t = 0) et de i (t = 0). 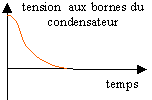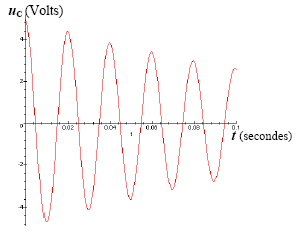- En déduire les valeurs de U0 et j. On réalise l’expérience décrite ci dessus uc (t) est enregistrée grâce à un système d’acquisition de données. L’allure de la courbe est donnée ci-dessous. Cette courbe est-elle conforme au modèle proposé pour ce circuit ? Pourquoi ? corrigé Exprimer uc en fonction de uL : uc + uL = 0 Exprimer i en fonction de uc : i = dq/dt ( q : charge de l'armature supérieure du condensateur) or q= Cuc ; i = dq/dt = Cduc/dt ; di /dt= d²q/dt² = Cd²uc/dt ² = Cu"c Exprimer uL en fonction de i : uL = L di/dt = LCu"c équation différentielle à laquelle obéit uc : uc + LCu"c = 0 ou bien u"c + 1/(LC) uc=0 expression de la fréquence propre en Hz : f= 1/(2p(LC)½)= 1/(6,28 (10-5)½=50,3 Hz. expression littérale du courant i en fonction du temps : uc= U0 cos ( 2pf t+j) i = Cduc/dt = -CU02pf sin ( 2pf t+j) uc (t = 0) = E ( condensateur chargé) et i (t = 0)= 0 ( la charge q n' a pas encore eu le temps de varier) uc(t=0)= U0 cos (j) = E donc cos (j) = 1 soit j =0 et U0= E Analyse de la courbe uc(t) : ce modèle ne convient pas : il implique la présence de résistor dans le dipole (LC), responsable de l'amortissement.
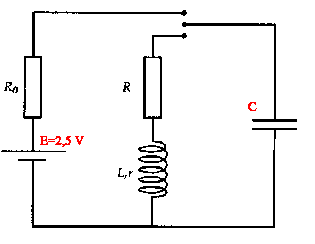
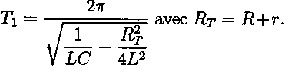
	On se propose d'étudier un capteur d'humidité. Etude du montage électrique : Un condensateur C est chargé à travers une résistance R0 = 100 W.En basculant l'interrupteur on décharge le condensateur dans une bobine (L= 100 mH, r) en série avec une résistance R.   L'expression de la pseudo période des oscillations est : - Vérifier que T1 a bien les unités d'un temps. - Exprimer la capacité C en fonction de T1, RT et L. - A quelle condition portant sur RT, C s'exprime-t-il en fonction linéaire de T1² ? 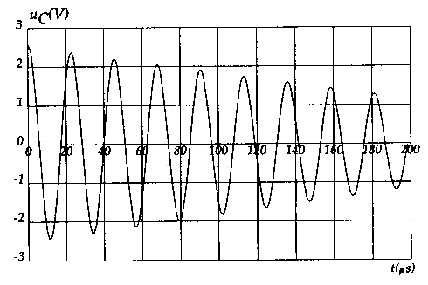L'enregistrement de la tension uC aux bornes du condensateur est représentée ci-dessous. La condition de la questuion 1 est-elle remplie ? Justifier. 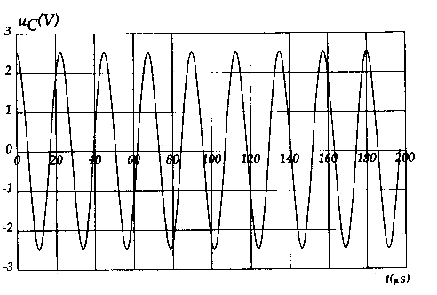Un montage amplificateur est inséré dans le circuit, l'enregistrement de la tension uC est représenté ci-dessous.La condition de la questuion 1 est-elle remplie ? Justifier. Combien vaut la période des oscillations de la tension uC ? En déduire la capacité C. Etude du capteur d'humidité : Un capteur d'humidité comporte en particulier un condensateur dont la capacité C augmente lorsque le taux d'humidité t augmente suivant la relation : C= (0,4 t + 104,8) pF avec t en %. Ce capteur était inséré dans le circuit précédent. Quel est le taux d'humidité ? corrigé 2 p est sans dimension ; L inductance : E=½LI² soit L= 2 E / I² : énergie (joule ) / intensité ² (Ampère) ² ; J A-2. Or énergie (J) = tension (V) * intensité (A) * durée (s) d'où L : V A-1 s. C capacité : E=½CU² soit C = 2 E /u² : énergie / tension² soit V-1A s LC : s² donc racine carré (LC) en seconde. RT résistance (ohms) = tension (V) / intensité (A) soit V A-1. RT/L s'exprime en seconde. T1²[1/(LC) - R²T/(4L²)]= 4 p ² ; T1²/(LC) - T1²R²T/(4L²)= 4 p ² ; 1/(LC) = 4 p ²/ T1² + R²T/(4L²) ; 1/C= 4 p ²L/ T1² + R²T/(4L) C= [4 p ²L/ T1² + R²T/(4L)]-1. si RT=0 alors C= T1² / (4 p ²L) la capacité est fonction linéaire de T1² graphe 1 : la condition RT=0 n'est pas vérifiée car la tension uC est amortie ( l'amplitude diminue) graphe 2 : la condition RT=0 est vérifiée car la tension uC n'est pas amortie ( l'amplitude reste constante) ; le montage avec amplificateur opérationnel compense à chaque instant les pertes d'énergie dans les résistances. 8 périodes correspondent à 180 ms soit T1 = 22,5 m s = 22,5 10-6 s. C=T1² / (4 p ²L) = (22,5 10-6)² / (4*3,14²*0,1)= 1,28 10-10 = 128 pF. C= 0,4 t+104,8 donne t = (C-104,8) / 0,4 =(128-104,8)/0,4 = 58%.
	retour -menu