d'après concours kiné Strasbourg 2004

Entre les points A et M de ce circuit la résistance équivalente a pour valeur :

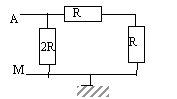
----> aide :
R et R en série équivalent à 2R
puis 2R et 2R en dérivation équivalent à R
1. R
2. 2R
3. 4R
4. 0,5R
Dans le cadre de ce circuit on a :
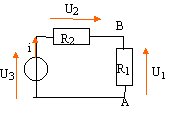
1. Uab= R1 i
2. Uab= - R1 i
3. U3=U1-U2
4. U3=U1+U2
On court-circuite un générateur à l'aide d'un fil de résistance négligeable.

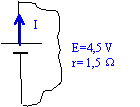
On peeut dire que :
1. Le générateur a une tension nulle entre ces bornes
2. Le générateur débite un courant maximal
3. Le générateur ne débite aucun courant
4. L'intensité du courant est I= 3A
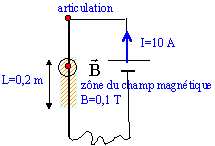
----> aide :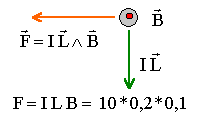

La force de Laplace :
1. fait dévier le barreau conducteur vers la gauche
2. a une intensité de 1 N
3. a une intensité de 0,2 N
4. a une intensité de 0,1 N
Un parachutiste considéré comme un solide ponctuel indéformable descend en translation vertical, en évoluant à vitesse constante, dans le référentiel terrestre :
1. Il n'est soumis qu'à son poids
2. il est soumis à des forces qui se compensent
3. La somme de son énergie cinétique et de son énergie potentielle de pesanteur restent constante
4. son énergie potentielle de pesanteur diminue
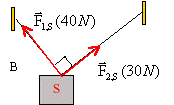
Le système est suspendu à deux cables dans un train et étudié dans le référentiel terrestre galiléen. Le poids de (S) n'est pas représenté :
----> aide
à l'équilibre :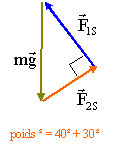
1. si S est immobile, le poids a pour valeur 50 N
2. si S est immobile, le poids a pour valeur 70 N
3. si S est embarqué dans un train et que S se déplace à présent en ligne droite sans accélér ni ralentir, on peut déduire que les trois forces qui agissent sur S se compensent
4. Quelque soit le mouvement de S les trois forces qui s'exercent sur lui se compenseront toujours
On note f= OF' la distance focale. Le point A émet de la lumière.

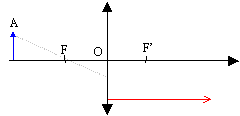
----> aide :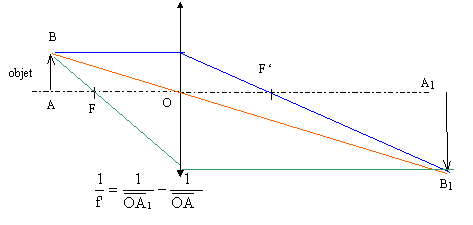
1. Le rayon émit par A et passant par F ressort de la lentille parallèlement à l'axe optique principal
2. Le rayon lumineux tracé après la lentille est émis par A
3. La relation de conjugaison est la suivante :
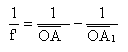
4. Tout rayon passant par F' est passé par A auparavant
On charge un condensateur sous une tension Uo = 10 V à travers un résistor R= 10 kimoohms. A l'instant t=0 la charge du condensateur est nulle. On visualise la tension aux bornes du condensateur :

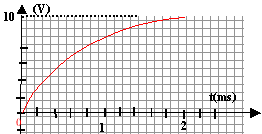
-----> aide :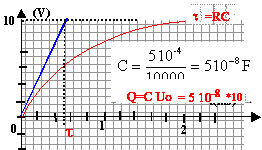
1. La constante de temps vaut 1 ms.
2. la capacité vaut C= 50 nF
3. au bout d'un temps très long, la charge du condensateur vaut 5 10^ -7 C
4. au bout d'un temps très long, l'intensité du courant est nulle
Deux noyaux de deutérium (H : A=2 et Z=1) fusionnent pour produire du tritium (H : A=3 et Z=1= et de l'hydrogène (H : A=1 et Z=1). Les énergies de liaison par nucléon sont 1,1 MeV pour le deutérium et 2,83 MeV pour le tritium
----> aide :
énergie de la réaction :
3 nucléons (tritium) * 2,83 - 2*2 nucléons (deutérium) fois 1,11
1. Le noyau de deutérium contient un proton et deux neutrons
2. Il y a formation d'un proton au cours de cette réaction
3. L'énergie libérée par la réaction est égale à 4,05 MeV
4. pendant cette fusion la masse se conserve
Un vibreur est relié à l'ectrémité S d'une corde. A l'instant t=0, le vibreur est mis en mouvement. l'aspect de la corde à t = 350 ms est représenté ci-dessous. L'origine des abscisses x=0 correspond à la position de l'ectrémité S .

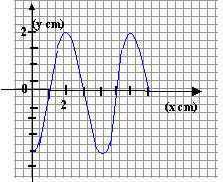
----> aide :
le point M de la corde situé à 0,07 m de S reproduit le mouvement de S avec un retard de 0,35 s.
c= 0,07/0,35 = 0,2m/ s.
longueur d'onde 0,04 m ( lecture graphe entre deux maximum)
période : T= longueur d'onde (m) / célérité (m/s ) = 0,04 / 0,2 = 0,2 s.
1. A t=0 le vibreur est mis en mouvement vers le bas.
2. La longueur d'onde est 4 cm.
3. La période est 0,2 s.
4. La célérité de l'onde est 8 10^ -3 m/s
On étudie la propagation le long d'une corde élastique. A la date t=0 le front de la perturbation quitte l'extrémité S de la corde. A la date t1= 1,5 s, on prend une photographie instantanée de la corde (figure 1). On prend un second cliché à la date t2= 2,25 s (figure 2)

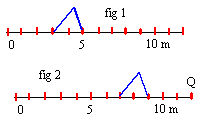
----> aide :
le front de l'onde parcourt 3 m en 0,75 s
célérité : 3/0,75 m/s.
1. L'onde qui se propage est une onde longitudinale.
2. La célérité de l'onde est 4 m/s
3. Le point Q commence à bouger à la date t= 3 s.
4. Le point Q cesse de bouger à la date t= 3,2 s.
Un conducteur réduit sa vitesse de 86 km/h à 50 km/h en 4 s. Le système (automobile + conducteur) a une masse M= 1000 kg et la valeur de la force de frottement f est supposée constante.
----> aide :
mettre les vitesses en m/s en divisant par 3,6
variation de vitesse ( 86-50)/3,6 = -10 m/s
accélération = variation de la vitesse / durée de la variation
------
somme de forces ( projection sur un axe horizontal) = M * accélération
f = M a ; f= 1000*2,5
1. La valeur de l'accélération est 2,5m/s²
2. La valeur de l'accélération est 9m/s²
3. f= 9000 N
4. f=9800 N soit le poids de la voiture
Une brindille de masse m=4 g tombe sans vitesse initiale d'une hauteur h=8 m. pendant sa chute elle est soumise à une réaction résistante due à l'air de valeur F= 24 mN. Dans le référentiel terrestre galiléen, le mouvement de son centre d'inertie est rectiligne vertical. g= 10 m/s²
----> aide :
chute libre : solide soumis uniquement à son poids.
poids - frottement = m a ( axe vertical vers le bas)
a= g-f/m = 10 - 24/4
h= ½at² soit t²= 2h/a = 16/4=4
vitesse v=at = 4*2 m/s
1. La brindille est en chute libre
2. son accélération vaut 4 m/s²
3. la durée de la chute vaut 4 s.
4. la vitesse au sol vaut 8 m/s.
Un avion volant horizontalement à une altitude de 2000 m à vitesse constante largue une charge. La résistance de l'air exercée sur la charge est négligeable. Le champ de pesanteur est uniforme et le mouvement de l'avion n'est pas modifié. Le mouvement de la charge est :
1. le même que celui de l'avion
2. verticale uniformément accélé dans le référentiel de l'avion
3. de même vitesse horizontale que l'avion dans le référentiel terrestre
4. rectiligne uniformément accéléré dans le référentiel terrestre
On considère le mouvement du centre d'inertie d'un projectile en chute libre lancé dans le champ de pesanteur uniforme avec une vitesse initialeVo non nule faisant un angle a avec l'horizontale. La portée ( abscisse du point où la trajectoire recoupe l'axe horizontale passant par l'origine du tir) de ce projectile, à une valeur V0 donnée :
----> aide :
portée : Vo² sin (2a) / g
portée maximale si l'angle de tir vaut 45° .
1. ne fait que croître lorsque l'angle de tir augmente
2. est maximale pour a=45°.
3. vaut Vo²/g si l'angle de tir vaut 45°.
4. est égale pour deux valeurs complémentaires de l'angle de tir.
On étudie le mouvement de 4 satellites naturels de Jupiter dans un référentiel jupitérocentrique. On considère que :
- le centre d'inertie d'un satellite est circulaire uniforme autour de Jupiter.
- chaque satellite n'est soumis qu'à la seule force gravitationnelle de Jupiter
- les astres ont une répartition de masse à symétrie sphérique.
----> aide
vitesse du satellite = racine carrée ( G Masse jupiter / distance des centres))
1. le satellite le plus rapide est le plus proche de Jupiter.
2. le satellite le plus rapide est le plus loin de Jupiter.
3. la vitesse du satellite dépend de sa masse
4. La vitesse du satellite dépend de la masse de Jupiter
Si on multiplie par 4 la longueur d'un pendule simple, sa fréquence est :
----> aide :
période = 2 pi racine carrée (L/g)
fréquence = 1/(2 pi) racine carrée (g/L)
1. multipliée par deux
2. multipliée par 4
3. divisée par 2
4. divisée par 4.
Un solide de masse m= 100 g glissant sans frottement sur une tige horizontale est accroché à un ressort idéal de raideur k= 100 N/ m. Il est lancé à la vitesse V= 1 m/s à partir de sa position d'équilibre
----> aide :
conservation de l'énergie mécanique
½mV² = ½k a² avec a : amplitude en m
a = racine carrée (m/k) V = racine carrée (0,1/100)*1= 0,0316 m
énergie potentielle maxi = énergie cinétique maxi = ½*0,1*1² = 0,05 J = 50 mJ.
1. l'allongement maximal ou amplitude est 3,2 cm
2. l'allongement maximal est 10 cm
3. l'énergie potentielle élastique maximale vaut 0,5 J
4. l'énergie potentielle élastique maximale vaut 50 mJ
On observe la propagation d'ondes mécaniques à l'aide d'une cuve à onde. L'onde rectiligne aborde une ouverture et poursuit sa propagation après l'ouverture comme indiqué sur la figure .

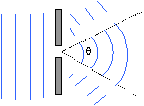
----> aide
angle téta = longueur d'onde divisé par largeur de l'ouverture.
1. Le phénomène observé est une réfraction de l'onde mécanique en présence de l'ouverture.
2. La taille de l'ouverture modifie la valeur de l'angle téta.
3. lorsque la taille de l'ouverture diminue la longueur d'onde de l'onde transmise augmente.
4. dans lke cas d'une petite ouverture, de taille nettement inférieure à la longueur d'onde de l'onde incidente, l'ouverture se comporte comme une source d'onde circulaire
Une onde lumineuse provenant d'une lampe spectrale comporte une seule radiation visible de longueur d'onde 590 nm. Le faisceau de lumière produit est rectiligne. On éclaire une fente de largeur a variable et on observe l'intensité lumineuse sur un écran placé à la distance D= 2m de la fente.
----> aide
diffraction si une onde rencontre un obstacle (ou une fente) dont les dimensions sont du même ordre de grandeur que la longueur d'onde.
1. On réalise a= 1 mm. Il n'y apas de phénomène de diffraction car la largeur de la fente est beaucoup plus grande que la longueur d'onde.
2. On réalise a = 0,1 mm. La position angulaire du premier maximum de diffraction, repéré par rapport à l'axe du dispositif est donée par téta = lambda/ largeur fente
3. La diffraction a toujours lieu lorsque la lumière rencontre un obstacle
4. Lorsque la lumière comporte plusieurs radiations, il n'y a plus de phénomène de diffraction
A une radiation monochromatique de fréquence f on associe un photon d'énergie E(joule). On note h : constante de Plank, T période et c célérité de la lumière dans le vide.
1. E= h/ fréquence
2. E= h fois fréquence
3. E= h c / fréquence
4. E= hT / fréquence
Les niveaux d'énergie de l'atome d'hydrogène ( eV) sont donnés par : E= -13,6 / n².
Le nombre n est un entier. n=1 correspond à l'atome pris dans son état fondamental. Les photons visibles ont des énergies comprises entre 1,6 et 3,1 eV.
1. L'énergie d'ionisation de l'atome d'hydrogène vaut 13,6 eV
2. Si n>1 l'atome est dans un état excité
3. La transition entre le niveau n=2 et le fondamental correspond à une radiation du spectre visible
4. Le niveau n=2 correspond à une énergie de 3,4 eV
Un circuit comporte un condensateur de capacité C et une bobine idéale d'inductance L. Le condensateur est initialement chargé sous une tension E. On observe l'évolution de sa charge q(t) portée par l'armature initialement positive. Elle a pour expression :
----> aide :
oscillateur électrique non amorti
q(t) = CE cos ( 1/ racine carré (LC)) t)
à t=0 la charge initiale vaut Qo=CE
1. q(t) = CE exp(-t / (LC))
2. q(t) = CE cos ( 1/ racine carré (LC)) t)
3. q(t) = CE sin ( 1/ racine carré (LC)) t)
4. q(t) = CE(1-exp(-t / (LC))
On réalise le montage ci-dessous dans lequel le condensateur est initialement chargé. On ferme l'interrupteur et on relève l'intensité du courant qui traverse la bobine à l'aide d'un oscilloscope ( figure 1)
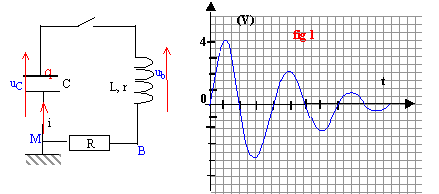
1. les oscillations électriques sont amorties, le régime est pseudopériodique.
2. La tension aux bornes de la bobine est donnée par : u= Ldi/dt+ r i
3. la tension aux bornes du condensateur est liée à l'intensité du courant i par la relation i= Cdu/dt
4. l'énergie électrique est dissipée par la bobine
On réalise un circuit comportant trois ampoules identiques notés A1, A2, A3. Les ampoules A1 et A2 sont mises en série avec deux bobines d'inductance respectives L1 et L2 et de résistance r. On ferme l'interrupteur K.

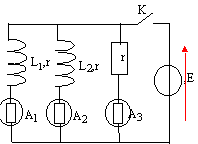
On donne L1 = 3 L2 ; r= 10 ohms et E= 10 V.
----> aide :
les bobines introduisent un retard à l'établissement du courant ; retard d'autant plus grand que l'inductance est grande.
en régime permanent les bobines se comportent comme des résistors avec r = 10 ohms.
1. L'ampoule A3 brille moins fort que A1 et A2.
2. l'ampoule A3 s'allume avant A1 et A2.
3. l'ampoule A1 met trois fois plus de temps à s'allumer que l'ampoule A2.
4. Au bout d'un temps suffisamment long l'intensité du courant délivré par le générateur devient constante en restant inférieure à 3 A.