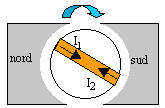Aurélie jan 04

mécanique - électricité - chimie

d'après concours masso-kinésithérapie Rennes

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.


Entre la terre et la lune il existe un point où les forces de gravitation exercées par les deux astres sur un objet de masse m se compensent.

  1. Montrer que cela est possible en vous aidant d'un schéma.
  2. A quelle distance de la terre se trouve ce point ?

Données : Mterre = 5,98 1024 kg ; M lune = 7,4 1022 kg ; intensité de la force de gravitation exercée par la terre sur la lune : F= 2 1020 N ; constante de gravitation G= 6,67 10-11 SI. 

corrigé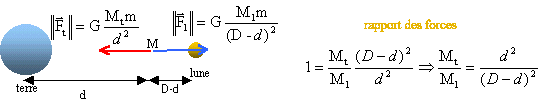

D :distance terre lune.

avec Mterre / M lune = 5,98 1024 / 7,4 1022 = 80,81.

prendre la racine carrée de l'expression : 80,81 = (d/D-d)²

soit 9 = d/(D-d ) ; 9D-9d = d ; d= 0,9 D

Comment calculer D, distance terre lune ?

force exercée par la terre sur lea lune GMterreMlune / D²= 2 1020.

D²= 6,67 10-11 * 5,98 1024*7,4 1022 / 2 1020 = 1,47 1017.

D =3,84 108 m d'où d = 0,9*3,84 108 =3,45 108 m.

 

  1. Une sphère pleine, homogéne de diamètre d=2 cm est suspendue à un ressort à spires non jointives de constante de raideur k=0,3 N/m et de longueur à vide l0 = 10 cm. Lorsque la sphère est à l'équilibre , le ressort a une longueur l=15 cm.
    - Déterminer l'expression littérale de la masse volumique de la sphère. Calculer sa valeur.
  2. La sphère est déchrochée du ressort et flotte sur un liquide de masse volumique r1. A l'équilibre la sphère est immergée au 1/3 de son volume total.
    - Déterminer l'expression littérale de la masse volumique du liquide. Calculer sa valeur.
  3. Une sphère métallique pleine et homogène de rayon r= 3 mm, de masse m =1 g est lâchée sans vitesse initiale à l'instant t=0 dans une éprouvette contenant un liquide de masse volumique r. A t=0 le centre d'inertie de la sphère se trouve à la distance r de la surface du liquide.
    - Quelle doit être la valeur maximale de r si l'on veut que la sphère tombe au fond de l'éprouvette ?
    - Lors du mouvement de la sphère, établir l'équation différentielle du mouvement relative à sa vitesse.
    - En supposant l'éprouvette assez profonde, la bille atteint une vitesse limite. Déterminer l'expression littérale de cette vitesse. La calculer.
    - En utilisant la méthode d'Euler avec un pas Dt=0,005 s déterminer la vitesse de la sphère à t=0,025 s.

Données : force de frottement f= (2,31ph0,6 d1,4 r 0,4 ) v1,4 ; viscosité h =0,03 Pa s ; r = 1000 kg/m3 ; d : diamètre de la sphère ; v : vitesse de la sphère ; g=9,81 m/s².

corrigé
A l'équilibre le poids de la sphère et la tension du ressort ont la même valeur

mg = k(l-l0)

masse (kg) = volume sphère (m3) * masse volumique sphère(kg/m3) ; m = 4/3pr3 m.

4/3pr3 mg = k(l-l0) soit m = 3 k(l-l0) / (4pr3 g )

m = 3*0,3(0,15-0,1) / (4*3,14* (10-2)3*9,81)=366 kg/m3.

A l'équilibre la sphère est soumise à deux forces opposée son poids P et la poussée d'Archimède P.

P=mg = V mg ; avec V : volume de la sphère (m3)

P = r1 gVimmergé = r1 gV/3

P=P ; V mg = r1 gV/3 soit r1 = 3m = 366*3 = 1098 kg/m3.

La sphère tombera au fond à condition que le poids soit supérieur à la poussée d'Archimède.

poids : P=mg =10-3*9,8 = 9,8 10-3 N.

poussée : P = r gVsphère = r g 4/3pr3 .

9,8 10-3 > r g 4/3pr3 soit r <3*9,8 10-3 / (g 4pr3 )

r <3 10-3 / ( 4*3,14*(310-3)3 )

r < 8846 kg/m3 .

Lors de la chute, la sphère est soumise à :

son poids, vertical vers le bas P=mg

la poussée d'Archimède, verticale vers le haut : P = r g4/3pr3

la force de frottement fluide, verticale vers le haut : f = (2,31ph0,6 d1,4 r 0,4 ) v1,4 ;

Ecrire la seconde loi de Newton suivant un axe verticale orienté vers le bas : P-P-f = ma = mdv/dt

mg - r g4/3pr3 - (2,31ph0,6 d1,4 r 0,4 ) v1,4 = m dv/dt

dv/dt + (2,31ph0,6 d1,4 r 0,4 ) / m v1,4 = g - r g 4/(3m)pr3 .

la vitesse limite étannt atteinte le terme dv/dt est nulle :

(2,31ph0,6 d1,4 r 0,4 ) / m vl1,4 = g - r g 4/(3m)pr3 .

vl1,4 = (mg - r g 4/3pr3) / (2,31ph0,6 d1,4r0,4 ).

mg=9,8 10-3 N ; r g 4/3pr3 = 103*9,8*4/3*3,14*(3 10-3)3=1,1 10-3 N

(2,31ph0,6 d1,4r0,4 ) = 2,31*3,14*0,030,6*(6 10-3)1,4*10000,4=7,253*0,122*7,75 10-4*15,84=1,08 10-2.

vl1,4 =(9,8-1,1)10-3 / 1,08 10-2=0,8 d'où vl = 0,85 m/s.

méthode d'Euler :

Dv = v(t+Dt)-v(t)

v(t+Dt) = v(t) + Dv (1)

d'après l'équation différentielle : Dv / Dt + 1,08 10-2 / 10-3 v1,4 = 9,8-1,1

Dv / Dt + 10,8 v1,4 = 8,7

Dv = (8,7- 10,8 v1,4 )Dt (2)

à t=0 la vitesse initiale est nulle et Dv (0)=8,7*0,005 = 0,0435 m/s

repport dans (1) : v(0,005) = 0 + 0,0435 = 0,0435 m/s.

à t=0,005 : v1,4 = 0,04351,4 = 0,0124 et Dv (0,005)=(8,7-10,8*0,0124)*0,005 = 0,0428 m/s

repport dans (1) : v(0,01) = 0,0435 +0,0428= 0,0863 m/s.

à t=0,01 : v1,4 = 0,08631,4 = 0,0324 et Dv (0,01)=(8,7-10,8*0,0324)*0,005 = 0,04175m/s

repport dans (1) : v(0,015) = 0,0863 +0,04175= 0,128 m/s.

à t=0,015 : v1,4 = 0,1281,4 = 0,0563 et Dv (0,01)=(8,7-10,8*0,0563)*0,005 = 0,0404m/s

repport dans (1) : v(0,02) = 0,128 +0,0404= 0,168 m/s.

à t=0,02 : v1,4 = 0,1681,4 = 0,0823 et Dv (0,01)=(8,7-10,8*0,0823)*0,005 = 0,039m/s

repport dans (1) : v(0,025) = 0,168 +0,039= 0,207 m/s.


  1. Un conducteur indéformable est formé de trois barres AM, MN, NC ; il est mobile autour d'un axe D horizontal et a une masse très faible. des fils souples connectés en A et C permettent de faire circuler un courant allant de M vers N. En l'absence de courant, le cadre est situé dans le plan vertical passant par l'axe D. A t=0 on fait passer un courant d'intensité I=5 A; MN= 10 cm
    -Quelles doivent être les caractéristiques du champ magnétique qui règne dans l'espace où se trouve le cadre si on veut que la force exercée en M', milieu de MN, soit perpendiculaire au plan vertical défini par les points A, M, N à t=0, dirigée vers l'avant de la feuille telle que F= 0,04 N
    - Représenter le champ magnétique B.
    - Représenter les forces électromagnétiques en A' milieu de [AM] et en N' milieu de [NC].
  2. Quelle est le nom de chaque partie du moteur ?
    - Quelle est la principle convertion d'énergie réalisée lors du fonctionnement du moteur ?
    - Pour que le cadre tourne dans le sens proposé, quel est le sens du courant I1 ou I2 ?
    Le champ magnétique B est radial entre les pièces polaires nord et sud.
corrigé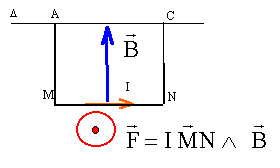

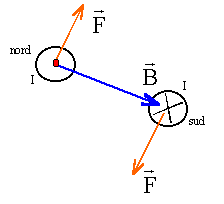
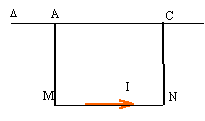
F= I*MN*B d'où B= F/(MN*I)= 0,04/(5*0,1) = 0,08 T

les vecteurs B et AM et CN sont colinéaires : donc les branches AM et CN ne sont soumisent à aucune force électromagnétique.

rotor partie mobile ; stator : partie fixe, pièces polaires.

Le moteur convertit de l'énergie électrique en énergie mécanique.

le courant va dans le sens I1.


On prépare 100 mL de solution de dichromate de potassium en dissolvant 0,470 g de solide dans une fiole jaugée. Avec cette solution on dose des ions Fe2+ contenus dans une solution S.La prise d'essai est 20 mL. Le volume versé à l'équivalence est 15 mL Quelle est la concentration en ion fer II de la solution S ?
masse molaire dichromate de potassium 294,19 g/mol ; fer : 55 g/mol ; soufre : 32,07 g/mol ; oxygène : 16 g/mol.

couples redox : Cr2O72- / Cr3+ ; Fe3+ / Fe2+.

corrigé
Cr2O72- + 6e- + 14H+ = 2Cr3+ + 7H2O

6Fe2+ = 6Fe3+ + 6e-

Cr2O72- + 6Fe2+ + 14H+ = 2Cr3+ + 7H2O + 6Fe3+

Qté de matière dichromate de potassium : 0,47 / 294,19 = 1,6 10-3 mol.

[Cr2O72-]=1,6 10-3 / 0,1 =0,016 mol/L
Cr2O72- ajouté
+ 6Fe2+
initial
0
n mol
en cours
x mol
n-6 x
équivalence
xéqui = 0,016* 15 10-3 = 2,4 10-4 mol
n-6xéqui=0
n = 6 xéqui=6*2,4 10-4 =1,44 10-3 mol

[Fe2+]= 1,44 10-3 /20 10-3 = 7,2 10-2 mol/L.

On réalise le mélange de 200 mL de solution de chlorure de potassium à 5 10-3 mol/L et de 800 mL de solution de chlorure de plomb à 1,25 10-3 mol/L. Quelle est la conductivité de la solution obtenue ?

lK+ = 74 10-4 S m2 mol-1 ; lCl- = 76 10-4 S m2 mol-1 ; lPb2+ = 140 10-4 S m2 mol-1 .

corrigé
conductivité s = lK+ [K+] + lCl-[Cl-] + lPb2+ [Pb2+]

volume du mélange : 1 L = 10-3 m3 ; ; [K+] = 5 10-3 *0,2 / 10-3 = 1 mol/m3.

[Pb2+] = 1,25 10-3 *0,8 / 10-3 = 1 mol/m3.

les ions chlorure sont issus des deux solutions:

PbCl2 solide = Pb2+ + 2Cl- ;

[Cl-] = ( 5 10-3*0,2 + 2 *0,8*1,25) / 10-3 = 3 mol/m3.

s = 74 10-4 * 1 + 76 10-4 * 3 + 140 10-4 *1 = 442 10-4 = 4,42 10-2 Sm-1.

On se propose de vérifier le degré de pureté du bicarbonate de soude NaHCO3.

Etape 1 : réaction avec l'acide chlorhydrique : on fait réagir 1 g de bicarbonate de soude avec 25 mL d'acide chlorhydrique à 1 mol/L. Soit S1 la solution obtenue après réaction. Cette solution est chauffée pendant quelques minutes.

Etape 2 : titrage de l'excès d'acide chlorhydrique par une solution de soude. : on verse la solution S1 dans une fiole jaugée et on complète à 200 mL avec de l'eau distillée. Soit S2 cette solution. On dose 20 mL de S2 avec une solution de soude de concentration cb=0,1 mol/L en utilisant un indicateur coloré.

  1. Ecrire l'équation de la réaction entre l'ion hydrogénocarbonate et la solution d'acide chlorhydrique. Calculer sa constante d'équilibre.
    - Pourquoi chauuffe-t-on S1 ? Expliquer.
  2. Ecrire l'équation de la réaction de titrage.
    - A l'équivalence véqui = 13,6 mL. Déterminer la concentration en ion oxonium de la solution S2.
  3. Le degré de pureté est défini par d=m/100 où m est la masse en grammes de NaHCO3 contenue dans 100 g de'échantillon. En déduire le degré de pureté de cet échantillon.

masse atomique molaire (g/mol) Na=23 ; H=1 ;O=16 ; C=12.

couples CO2, H2O / HCO3- pKa = 6,4 ; HCO3- / CO32- pKa = 10,3

  1.  
corrigé
HCO3- + H3O+ = CO2 + 2H2O

CO2 + 2H2O = HCO3- + H3O+ ; Ka= [HCO3- ][H3O+] / [CO2]

Kéqui= [CO2] / ([HCO3- ][H3O+]= 1/Ka = 106,4 = 2,5 106.

Le chauffage élimine le CO2 dissout : celui ci est un acide qui pourrait réagir avec la soude dans l'étape 2 et fausser le dosage.

HO- + H3O+ = 2H2O

à l'équivalence acide-base la quantité de matière d'ion oxonium est éagle à la quantité de matière d'ion hydroxyde ajouté.

cava= cbvéqui soit ca = 13,6 10-3 *0,1 / 20 10-3 =6,8 10-2 mol/L

Qté de matière d'ion oxonium en excès dans 200 mL ( fiole jaugée)

0,068*0,2 = 0,0136 mol

Qté de matière d'ion oxonium apporté par l'acide (étape 1) : 0,025*1 = 0,025 mol

Qté de matière d'ion oxonium ayant réagi (étape 1) : 0,025-0,0136 = 0,0114 mol

Qté de matière hydrogénocarbonate de sodium :0,0114 mol

masse molaire NaHCO3: 23 + 1+12+3*16 = 84 g/mol

masse hydrogénocarbonate pur dans 1 g d'échantillon : 84*0,0114 = 0,958 g

degré de pureté : 0,958 ou 95,8 %.

La combustion complète dans le dioxygène d'une masse m0 = 1g d'un ester dont la chaîne carbonée ne comporte pas de liaison multiple, ni cycle, a conduit à la formation d'une masse m=2,157 g de CO2.
- Déterminer la formuke brute de l'ester.

- Ecrire les formules possibles de l'ester sachant que l'hydrolyse donne de l'acide méthanoïque.

corrigé
formule brute de l'ester : CnH2nO2.

combustion : CnH2nO2 + (1,5 n -1) O2 = n CO2 + n H2O.

Qté de matière CO2 : 2,157 / 44 =0,049 mol

donc d'après l'équation de réaction : 0,049 / m m ol d'ester

Qté de matière ester ( masse molaire M = 12n + 2n +32 = 14 n+32) : 1/M mol

par suite : 1/M=0,049/n soit n/0,049 = M ; 20,4 n = 14 n+32 soit n = 5

H-COO - CH2-CH2-CH2-CH3 méthanoate de butyle

H-COO - CH2-CH (CH3)2 méthanoate de 2-méthylpropyle

H-COO - CH(CH3)-CH2 -CH3 méthanoate de 1-méthylpropyle

H-COO - C(CH3)3 méthanoate de 2,2-diméthyléthyle

retour -menu