|
étude d'une bobine -mouvement d'une bille- estérification et cinétique - zone de virage d'un indicateur coloré En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||
| .
. |
|||||||||||||||||||||
|
|||||||||||||||||||||
|
|
Etude d'une bobine (5 points)
corrigé En régime permanent et en courant continu la bobine la tension aux bornes de la bobine est : U=rI soit r = U/I = 5/0,1 = 50 W. à l'ouverture de l'interrupteur la tension aux bornes de la bobine est : u = LDi/Dt + r i voisin de L Di/Dt avec |Di |= 0,1 A L= u Dt / Di = 500 *10-4 / 0,1 = 0,5 H. On observe alors une étincelle de rupture aux bornes de l'interrupteur : pour l'éviter monter une diode " dite de roue libre" en dérivation sur la bobine. constante de temps : t = L/r = 0,5 / 50 = 10-2 s = 10 ms. L = uL= u Dt / Di homogène à : [V] [s] [A]-1. r = U/I homogène à : [V] [A]-1. donc L/r homogène à un temps. la constante de temps permet de connaître la durée du régime transitoire ( 5 fois la constante de temps) pendant laquelle la bobine stocke de l'énergie à la fermeture de l' interrupteur ; au dela de 5t le régime permanent est établit. énergie stockée par la bobine : ½LI²max = 0,5*0,5*0,1²= 2,5 10-3 J. à l'ouverture du circuit cette énergie peut être libérée dans un petit néon provoquant un flash.
|
||||||||||||||||||||
|
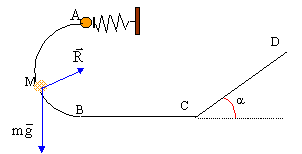
Etude d'une petite bille 5 points A- mise en mouvement de la bille : Un ressort de masse négligeable, à spires non jointives, a un coefficient de raideur k= 40 N/m et une longueur à vide l0= 20 cm. L'axe du ressort est horizontal. Il est fixé à son extrémité droite par un support fixe. A son extrémité gauche, une bille de masse m= 50 g est placée contre une butée P. Ce ressort va être utilisé pour lancer la bille dans une gouttière. On comprime le ressort ; sa longueur devient l= 8cm ; on libère le système. La bille quitte la butée lorsque le ressort reprend sa longueur initiale. En supposant les frottements négligeables, établir l'expression littérale de la vitesse vA avec laquelle la bille quitte le ressort puis effectuer l'application numérique. 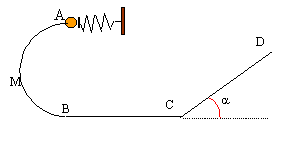 B- mouvement de la bille dans la gouttière située dans un plan vertical : La gouttière ABCD sert de parcours à cette bille supposée ponctuelle. g= 9,8 m/s². Les frottements sont négligés , la gouttière étant parfaitement lisse. AB est un demi cercle de rayon r= 0,5 m. La bille part de A avec la vitesse vA précédente.
corrigé En absence de frottement l'énergie mécanique du système {bille + ressort }se conserve : l'énergie potentielle élastique initiale se retrouve sous forme d'énergie cinétique quand la bille quitte la butée. ½k(l0-l)² = ½mv²A soit v²A =k(l0-l)² / m v²A =40(0,2-0,08)²/0,05 = 11,52 et vA = 3,4 m/s.
l'action du support R, perpendiculaire à la vitesse ne travaille pas. le travail du poids est moteur lors de la descente A--> B: mgAB= 2mgr la variation de l'énergie cinétique entre A et B est égal à la somme des travaux des forces : ½mv²B-½mv²A= 2mgr v²B= v²A + 2gr = 3,4² + 2*9,8*1=31,16 et vB= 5,58 m/s. entre B et C la bille est pseudo-isolée ( poids et action du plan se compensent) : donc entre b et C la vitesse garde la même valeur ( mouvement rectiligne uniforme d'après le principe d'inertie ou 1ère loi de Newton) Sur le plan incliné le travail du poids est résistant en montée : -mg CD sina. l'action du plan perpendiculaire à la vitesse ne travaille pas. la variation de l'énergie cinétique entre C et D est égal à la somme des travaux des forces : ½mv²D-½mv²C= -mg CD sina. v²D- v²C = -g CD sina soit CD=( v²C- v²D )/(g sina ) CD=( 5,58²-4²) / (9,8*0,707)= 2,18 m.
|
|||||||||||||||||||||
|
étude d'un estérification : ( 5 points) On se propose d'étudier la réaction d'estérification entre l'acide méthanoïque et l'éthanol
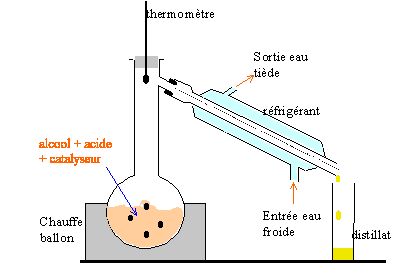
On chauffe à température constante plusieurs récipients contenant tous, initialement, un mélange de 0,5 mol d'acide ùméthanoïque et 0,5 mol d'éthanol. On dose à différentes dates l'acide restant dans chacun de ces mélanges et on en déduit la quantité de matière d'ester formé. On obtient la courbe ci-dessous. 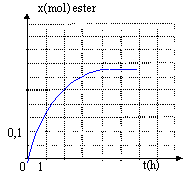
B cinétique de la réaction d'estérification :
corrigé HCOOH + CH3-CH2OH= HCOO-CH2-CH3 + H2O éthanol : 0,5 mol soit 0,5*46 = 23 g soit 23 / 0,79 =29,1 mL. acide méthanoïque : 0,5*46 = 23 g soit 23/1,22 = 18,85 mL. l'acide sulfurique catalyse la réaction : l'équilibre est atteint plus rapidement ; l'équilibre n'est pas modifié, donc on obtient la même quantité finale d'ester.
En élilminant l'un des produits au fur et à mesure qu'il se forme on déplace l'équilibre dans le sens direct, formation de l'ester. La réaction est alors totale. Le composé le plus volatil, dans ce cas l'ester, distille le premier : température constante 55°C On peut pour obtenir le même résultat introduire un réactif en large excès. On peut aussi remplacer l'acide méthanoïque par l'anhydride méthanoique HCO-O-OCH + CH3-CH2OH= HCOO-CH2-CH3 + HCOOH la vitesse volumique est la dérivée de l'avancement par rapport au temps. graphiquement elle est donnée par la valeur absolue du coefficient directeur de la tangente à la courbe x=f(t) à la date donnée. Au cours de la réaction cette vitesse diminue, puis s'annule : les quantités de matière des réactifs diminuent au cours du temps. A l'équilibre, durant le même temps il se forme autant d'ester et d'eau par la réaction directe qu'il n'en disparaît par la réaction inverse, l'hydrolyse de l'ester : donc la composition du mélange ne change pas.
|
|||||||||||||||||||||
|
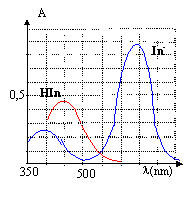
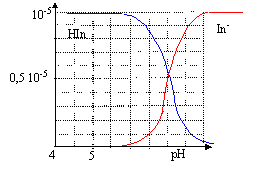
Détermination de la zone de virage d'un indicateur coloré (5 points) L'indicateur coloré étudié est le bleu de bromothymol(BBT) dont les formes acide et basique seront notées respectivement InH et In-. On réalise des solutions aqueuse de BBT dans lesquelles les quantités en HIn et In- sont variables ( la concentration molaire volumique apportée en indicateur étant constante). Ces solutions ont des colorations différentes, ce qui justifie que l'on utilise la spectrophotométrie pour réaliser l'étude.
corrigé HIn + H2O = In- + H3O+. K= [In-][H3O+] / [HIn] pH=pKa + log ([In-] / [HIn]) Une solution aqueuse de BBT contenant majoritairement l'acide est jaune : la forme acide présente un maximum d'absorption vers 450 nm, en conséquence le bleu est absorbé et la solution apparaît jaune, couleur complémentaire du bleu. l'étude doit être faite à une longueur d'onde pour laquelle l 'absorbance de la forme In- est maximale.( 620 nm) A cette longueur d'onde la forme HIn n'absorbe pas, en conséquence l'absorbance A est proportionnelle à la concentration en forme basique [In-] A = k [In-] et Amax = k [In-] max= kc Amax / A = [In-] max/ [In-] = c / [In-] d'où: [In-]= A/Amax c. de plus [HIn] + [In-]= c d'où [HIn] = c- [In-] = c-A/Amax c = (Amax -A)/Amax c. lorsque pH = pKa, alors [HIn] = [In-] : l'intersection des courbes donne la valeur du pKa soit environ pKa=7. zone de virage : 0,1 <[In-] / [HIn]<10. log 0,1<log[In-] / [HIn] <log 10 -1<pH-pKa<1 pKa-1 <pH <pKa+1 soit 6 <pH< 8.
|
|||||||||||||||||||||
|
|