Aurélie jan 04

Kiné Nantes d'après concours 2004

électricité -dipole (LC) - ballons atmosphériques - estérification -réaction avec l'ion argent

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


 

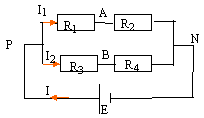E= 12 V ; R1 est la résistance d'un photorésistor ( conducteur dont la résistance varie avec l'éclairement) ; R2= 20 kW ; R3= 18 kW ; R4= 24 kW ;

  1. Exprimer la tension UAN en fonction de E, R1 et R2.
  2. Exprimer la tension UBN en fonction de E, R3 et R4.
  3. Exprimer la tension UAB en fonction de E, R1, R2, R3 et R4.
    - Etablir la condition sur R1, R2, R3 et R4 pour que UAB=0
    - Calculer R1 si UAB=0.
  4. Un voltmètre indique UAB= 100 mV. Calculer R1.

 

corrigé
UAN = R2I1 donne I1 =UAN / R2 ; UPN = E= UPA + UAN =(R1+R2)I1 ;

E = (R1+R2) UAN / R2 ; UAN = E R2 / (R1+R2)

UBN = R4I2 donne I2 =UBN / R4 ; UPN = E= UPB + UBN =(R4+R3)I2 ;

E = (R3+R4) UBN / R4 ; UBN = E R4 / (R3+R4)

UAB = UAN +UNB = UAN -UBN = E( R2 / (R1+R2)-R4 / (R3+R4))

réduire au même dénominateur :

UAB =E * (R2 (R3+R4)-R4(R1+R2)) / ((R1+R2)(R3+R4))

UAB =E(R2 R3-R4R1) / ((R1+R2)(R3+R4))

UAB s'annule pour R2 R3=R4R1 soit R1 = R2 R3/R4.

R1= 20*18/24= 15 kW.

si UAB = 0,1 V calcul de R1 :

0,1= E(R2 R3-R4R1) / ((R1+R2)(R3+R4))

0,1 = 12(20*18-24R1)/ (( R1+20)(18+24))=12(360-24R1)/ (( R1+20)*42)

0,1*42( R1+20)= 12(360-24R1)

4,2R1+84 = 4320-288R1 ; R1 = 4236 / 292,2= 14,5 kW.

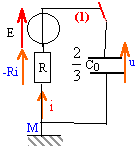
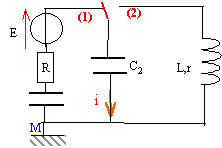Le générateur est une source de tension idéale de fem E. Les condensateurs ont les capacités C1=C0 et C2 = 2 C0. Initialement le commutateur est en position 1 et les condensateurs sont déchargés.

  1. A t=0 on bascule le commutateur en position 1. Les charges des condensateurs sont à chaque instant égale q1=q2 = q. Justifier.
    - Etablir l'équation différentielle vérifiée par la tension u aux bornes du condensateur de capacité C2.
    - Quelle est la tension U0 aux bornes du condensateur de capacité C2 quand les charges sont terminées ?
    - En fonction de C0 et E exprimer alors la quantité d'électricité Q0 débitée par le générateur, l'énergie EG fournie par le générateur, les énergie EC1 et EC2 stockées par les condensateurs.
    - Que représente la différence EJ= EG -(EC1+ EC2 ) ?
    - Calculer le rendement énergétique de cette charge (EC1+ EC2 )/EG
    - Vérifier que u(t) = U0(1-e-t/t) est solution de l'équation différentielle établie ci-dessus et en déduire l'expression de t en fonction de R et C0. Exprimer an fonction de t la durée nécessaire pour que la charge des condensateurs soit terminée ( on considère que la charge est terminée quand u>=0,99U0)
  2. La charge étant terminée on bascule le commutateur en position 2 et on choisit cet instant comme nouvelle origine des temps.
    - On suppose la résistance r de la bobine comme négligeable, établir l'équation différentielle vérifiée par la tension u.
    - Calculer la période propre T0 des oscillations.C0=10 mF et L= 0,5 H.
    - Etablir l'expression de u(t) et tracer u en fonction de t.
    - En réalité l'oscillogramme est celui représenté ci-dessous. Mesurer sur l'oscillogramme la pseudo-période T; la comparer à T0 et conclure.

    - Calculer les énergies E1, E2 et E3 stockées par le condensateur aux 1er, 2ème et 3ème maxima relatifs de u. Calculer E1/ E2 et E2, E3 et conclure.
    - On montre que ln(En/ En+1) = r/(2L)T ; en déduire la résistance r de la bobine.

 

corrigé
Les deux condensateurs sont montés en série, en conséquence les armatures ont en valeur absolue la même charge q.

ces deux condensateurs sont équivalents à un condensateur unique de capacité

C=C1C2/(C1+C2) = C02C0/(C0+2C0) = 2/3C0.

De plus C2=2C1 et q=Cu donc la tension aux bornes du condensateur de capacité C1 est égale à deux fois la tension aux bornes du condensateur de capacité C2.

 

u= -Ri +E avec i = dq/dt = q' = 2/3C0u'

u = -2/3RC0u' +E ; u +2/3RC0u' = E ;

u' +1/ t u =1,5 E/(RC0) avect = 2/3RC0.

la tension aux bornes du condensateur de capacité C2 vaut 1/3 u, soit U0= E/3 quand la charge est terminée.

celle aux bornes du condensateur de capacité C1 vaut 2/3 u, soit 2E/3 quand la charge est terminée ; la charge q0 de chaque armature est en valeur absolue : q0 = 2/3 C0E

énergie débitée par le générateur : q0E= 2/3 C0E²

énergie stockée dans chaque condensateur : ½CU²

½ C0(2/3E)² = 2/9 C0E² et ½ 2C0(1/3E)²=1/9C0E² ; total : 1/3 C0E² .

une partie de l'énergie fournie par le générateur est dissipée par effet joule dans le résistor R.

EJ= 2/3 C0E²-1/3 C0E² = 1/3 C0E² .

rendement énergétique de cette charge (EC1+ EC2 )/EG= 50%

équation différentielle vérifiée par la tension aux bornes du condensateur de capacité C2 :

u +2/3RC0u' = E /3 et u(t) = U0(1-e-t/t)

dériver u(t) par rapport au temps : u'= U0/ t e-t/t.

repporter u et u' par leur valeur dans l'équation différentielle:

U0(1-e-t/t) + 2/3RC0U0/ t e-t/t = E/3

U0-U0e-t/t+ 2/3RC0U0/ t e-t/t = E/3

par identification U0 = E/3 et -1+2/3RC0/ t =0 soit t = 2/3RC0.

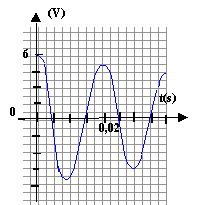
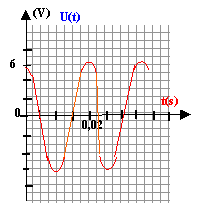
charge terminée si u=0,99 U0 soit 0,99 U0= U0(1-e-t/t) ;

0,99 = 1-e-t/t ; e-t/t = 0,01 ; -t / t = ln 0,01 soit t = 4,6 t.

commutateur en position 2 :

tension aux bornes de la bobine = tension aux bornes du condensateur =0

Ldi/dt = u avec i= -dq/dt ( signe moins car décharge)

i = -q' = -2C0u' soit i'= - 2C0u"

- 2LC0u" = u ou bien u"+1/(2LC0) u =0 ; on pose w0²= 1/(2LC0)

solution de cette équation du type u = E/3 cos(w0t), la phase à l'origine étant nulle car initialement le condensateur est chargé.

période T0= 2p/w0 ; w0= racine carrée[1/(2*0,5*10-5)]= 316,2 rad/s ; T0=6,28/316,2=0,0198s.

T et T0 ne différent que de 1%: l'amortissement doit être faible

premier maxima : 6 V ; second maxima 5,5 V; 3ème maxima : 5 V

énergies correspondantes stockées par le condensateur : ½(2C0)U²= C0U² = 10-5 U²

E1=36 10-5 J ; E2=30,25 10-5 J ; E1=25 10-5 J ;

E1/E2=1,19 ; E2/E3=1,21 ; E1/E2=E2/E3=1,2

ln 1,2 = rT/(2L) d'où r = 2L ln1,2 /T = 2*0,5 *0,182 /0,02= 9,1 W.

Ballon atmosphérique :

Pour étudier les hautes couches de l'atmosphère on utilise des ballons gonflés à l'hélium. Ces ballons sont constitués d'une enveloppe souple dilatable jusqu'à un volume Vlimite. Au sol ces ballons sont gonflés à un volume V < Vlimite. L'air et l'hélium sont des gaz parfaits de masses molaires Mair =29 g/molet MHe= 4 g/mol. Pour simplifier on admettra que ces gaz sont isothermes à la température T0=290 K. Pour l'altitude atteinte par ces ballons on peut considérer l'intensité de la pesanteur comme égale à g0=9,8 m/s². R= 8,314 J K-1 mol-1.

La masse volumique de l'air varie avec l'altitude suivant la relation rair = r0 e-z/H ; r0 masse volumique de l'air au sol ( z=0) et H=RT0/(Mairg0)=8400 m.

  1. Déterminer la valeur de r0 au sol sachant que la pression est P0=1013 hPa.
    - Donner la loi d'évolution de la pression P en fonction de P0, H et z.
  2. Donner l'expression de la masse volumique rHe de l'helium en fonction de rair, Mair et MHe.
  3. La masse du ballon vide et des instruments est m=200 kg. Déterminer en fonction de m, r0, Mair et MHe le volume minimale permettant le décollage du ballon. Calculer ce volume Vmini.
  4. Au sol le ballon est gonflé avec un volume d'hélium V0= 250 m3. Lorsque le ballon s'élève, l'enveloppe se dilate de V= V0 =250 m3 à V= 1000 m3, la pression à l'intérieur du ballon restant égale à la pression à l'altitude considérée.
    - Déterminer la masse d'hélium contenue dans le ballon.
    - Déterminer l'altitude pour laquelle V= 1000 m3.
corrigé
PV= nRT avec n = masse (g) / masse molaire (g/mol) = m/Mair.

r0 = m/V = P0Mair/(RT)

R= 8,314 ; T=290 K ; P= 1,013 105 Pa et Mair= 29 10-3 kg

r0 = 1,013 105*29 10-3/(8,314*290)=1,21 kg/m3.

rair = r0 e-z/H = P Mair/(RT) soit P= r0Mair/(RT) e-z/H .

or r0 = P0Mair/(RT) soit P0= r0Mair/(RT) ; P= P0e-z/H .

pour une mole de gaz parfait :quelconque r = M/Vmolaire.

rair = Mair/Vmolaire. rHe = MHe/Vmolaire. rHe =rair MHe/Mair= 1,21*4/29 = 0,167 kg m-3.

le ballon décolle lorsque la poussée d'Archimède due à l'air est supérieure au poids du ballon

Poussée au sol = poids du volume d'air déplacé par le ballon = rair Vmini g0.

poids =( m + rHe Vmini )g0

rair Vmini g0= ( m + rHe Vmini )g0 ; rair Vmini = m + rHe Vmini ;

volume minimal du ballon : Vmini = m / (rair -rHe )= 200 / (1,21-0,167) = 191,7 m3.

masse d'hélium contenue dans le ballon:

P0V0= m/MHe RT

m = P0V0MHe / (RT) avec MHe = 4 10-3 kg

m= 1,013 105*250*4 10-3/(8,314*290)= 42 kg.

PV= m/MHeRT, la température est supposée constante et P= P0e-z/H.

P0e-z/HV= m/MHeRT ; e-z/H = m/MHeRT / (P0V)

e-z/H = 42/0,004*8,314*290/(101300*1000)=0,25

z/H = -ln0,25 =1,386 ; z= 1,386 H = 1,386*8400= 11,64 km.

étude d'une estérification

 L'acide éthanoïque réagit avec l'éthanol suivant CH3-COOH+ CH3-CH2OH=H2O+E

  1. Donner la famille chimique, la formule semi-développée de E.
    - Donner le nom et la formule de deux isomères de E ; on proposera un isomère de la même famille que E et un autre d'une famille différente que l'on précisera.
  2. Lors d'un mélange initial composé uniquement de 10 moles d'acide éthanoïque et d'une mole d'éthanol, on obtient à l'équilibre 0,971 mole de E et 0,971 mole d'eau. Déterminer la composition complète à l'équilibre. En déduire la constante d'équilibre K de la réaction étudiée.
  3. On effectue un nouveau mélange constitué initialement de une mole d'acide éthanoïque pur,d'une mole d'éthanol, 3 moles d'eau et 3 moles de E.
    - Déterminer le quotient initial Qr i de la réaction.
    - Dans quel sens va évoluer la réaction chimique.
    - Donner la composition final lorsque l'équilibre est atteint.
  4. Citer deux moyens pour accéléer l'obtention de l'équilibre final sans le modifier.
  5. Le composé E peut être obtenu par réaction entre l'éthanol et un composé de formule C4H5O3.
    - Donner la formule semi-développée de ce composé. Quelle est sa famille chimique ?
    - Ecrire la réaction et préciser ces caractéristiques essentielles.
corrigé
ester : éthanoate d'éthyle CH3-COO-CH2-CH3.

un autre ester isomère le propanoate de méthyle CH3-CH2-COO-CH3.

un acide carboxylique isomère l'acide butanoïque CH3-CH2-CH2-COOH.

CH3-COOH
+ CH3-CH2OH
= H2O
+E
initial
10 mol
1 mol
0
0
en cours
10-x
1-x
x
x
équilibre
10-xéq= 9,029 mol
1-xéq = 0,029 mol
xéq = 0,971
xéq
K=[E]éq[H2O]éq /([CH3-COOH]éq[CH3-CH2OH]éq)= 0,971*0,971/(0,029*9,029)=3,6.

Qr i =[E]i[H2O]i /([CH3-COOH]i[CH3-CH2OH]i)= 3*3/1=9.

le quotient de réaction initial est supérieur à la constante d'équilibre, donc évolution dans le sens indirect, vers la gauche.
H2O
+ E
CH3-COOH
+CH3-CH2OH
initial
3 mol
3 mol
1
1
en cours
3-x
3-x
1+x
1+x
équilibre
3-xéq
3-xéq
1+xéq
1+xéq
3-0,38 = 2,62 mol
3-0,38 = 2,62 mol
1+0,38 = 1,38 mol
1,38 mol
1/ 3,6 =0,277=(1+xéq)²/(3-xéq)²

prendre la racine carrée : 0,527 = (1+xéq)/(3-xéq) ; 0,527(3-xéq) =1+xéq.

1,58 -0,527xéq= 1 + xéq soit xéq=0,38 mol.

à l'aide d'un catalyseur et en augmentant la température, l'équilibre est plus rapidement atteint ; sa composition n'est pas changée.

avec l'anhydride éthanoïque : CH3-CO-O-OC-CH3.

réaction totale, rapide, exothermique

CH3-CO-O-OC-CH3 +CH3-CH2OH -->CH3-COO-CH2-CH3 +CH3-COOH


Réaction avec l'ion argent
  1. Dans de l'eau distillée à 25°C, on introduit des cristaux de chlorure d'argent AgCl en excès. Il se produit la réaction de dissolution AgCl (s)=Ag+ + Cl-.  La conductivité de la solution saturée S ainsi obtenue est ss= 245mS/m. La conductivité de l'eau distillée utilisée est se= 70mS/m
    - Que représente la différence ss-se.
    - Calculer la concentration des ions Ag+ et Cl- dans la solution S.
    - Calculer la solubilité du chlorure d'argent en mol/L et en g/L
    - Calculer la constante d'équilibre KS associée à cette dissolution.
    masse atomique molaire Ag= 107,9 ; Cl =35,5 g/mol
    conductivité molaire mS m² mol-1 : lAg+= 6,19 ; lCl-= 7,63.
  2. On associe par un pont salin une demi-pile constituée d'une plaque de zinc dans 100 mL de solution de nitrate de zinc de concentration C0= 0,2 mol/L et une demi-pile constituée d'une tige d'argent dans 100 mL d'une solution de nitrate d'argent de même concentration C0. Un voltmètre placé aux bornes de la pile montre que l'électrode d'argent est la borne positive. La différence de potentiel entre les deux électrodes est : U= 1,56 +0,03 log([Ag+]²/[Zn2+]), les concentrations molaires s'exprimant en mol/L.
    - Calculer la tension initiale U0.
    - On fait débiter la pile dans un récepteur pendant une heure avec une intensité moyenne I= 482 mA. Ecrire les demi-équations électroniques des réactions se produisant à la surface des électrodes ; en déduire l'équation de la réaction chimique liée au fonctionnement de cette pile.
    ** Calculer la quantité d'électricité q débitée pendant l'heure de fonctionnement
    ** Calculer les concentrations [Ag+] et [Zn2+] après une heure de fonctionnement. En déduire la tension indiquée par le voltmètre.
    e= 1,6 10-19 C et NA= 6,02 1023 mol-1.
corrigé
la différence ss-sereprésente la conductivité due aux ions chlorure Cl- et argent Ag+.

ss-se= lCl- [Cl-]+lAg+[Ag+] avec [Cl-] =[Ag+] mol m-3.

ss-se = (lCl- +lAg+)[Ag+] soit [Ag+] = (245-70)10-6 / ((6,19+7,63)10-3)=0,175 / 13,82 =0,0127 mol m-3.

solubilité du chlorure d'argent : [Ag+] =1,27 10-2 mol m-3 = 1,27 10-5 mol/L.

masse molaire AgCl : 107,9+35,5 = 143,4 g/mol

solubilité : 143,4*1,27 10-5 = 1,82 10-3 g/L.

constante d'équilibre KS = [Ag+][Cl-] =1,27 10-5 *1,27 10-5 =1,6 10-10.

U0= 1,56 +0,03 log([Ag+]0²/[Zn2+]0)

[Ag+]0=[Zn2+]0=C0=0,2 mol/L

[Ag+]0²/[Zn2+]0= C0=0,2 ; log 0,2 = -0,7

U0= 1,56+0,03*(-0,7)=1,539 V.

à l'anode négative, oxydation du zinc : Zn (s)= Zn2+ +2 e-

à la cathode positive, réduction des ions argent : 2Ag++2 e- = 2 Ag(s)

bilan : 2Ag+ + Zn(s)= 2Ag (s) + Zn2+.

quantité d'électricité q = I t = 0,782*3600 = 1735,2 C.

la charge d'une mole d'électrons est en valeur absolue : 96500 C

Qté de matière d'électrons : 1735,2/96500 =1,8 10-2 mol.

Ag+ disparu : 1,8 10-2 mol.d'où [Ag+]fin = (0,1*0,2- 0,018)/0,1= 0,02 mol/L

Zn2+ apparu : 0,9 10-2 mol d'où [Zn2+]fin=(0,1*0,2+ 0,9 10-2 )/0,1= 0,29 mol/L

[Ag+]fin²/[Zn2+]fin= 0,02² /0,29 =1,38 10-3 ; log 1,38 10-3 = -2,86

Ufin= 1,56+0,03*(-2,86)=1,474 V.

retour -menu