physique d'après concours fesic 2004

Une perturbation de durée 20 ms est produite à la date t=0 à l'extrémité A d'une corde de longueur AB= 10 m. Une onde ainsi produite et elle se propage à la célérité v= 25 m/s.
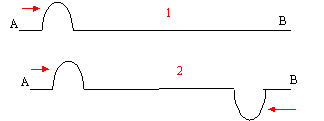
1. Le point M de la corde situé à 5 m de A est atteint par la perturbation à la date t=0,2 s.
  ----> aide :
  le point M reproduit le mouvement de la source A avec le retard AM/ v = 5/25
2. Le point M de la corde situé à 5 m de A est atteint par la perturbation à la date t=0,4 s.
3. A la date t=0 une perturbation est provoquée en A et une autre perturbation est provoquée à l'autre extrémité B de la corde. La célrité de l'onde ne dépend pas du sens de propagation.
4. A la date t=0 uneperturbation est provoquée en A et une autre perturbation est provoquée à l'autre extrémité B de la corde. Les deux ondes s'annulent après leur passage au milieu de la corde.
Le graphe suivant modélise l'aspect d'une corde soumise à une perturbation à la date t1.On note u le déplacement latéral de la corde. L'origine des dates correspond avec le départ de la perturbation du point source S. Le début du signal se propageant le long de la corde, arrive en un point M d'abscisse Xm=1,2 m à la date t2=t1+100 ms.
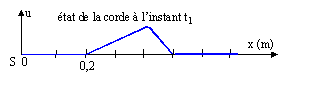
1. Cette onde est une onde mécanique longitudinale
2. La célérité v de la perturbation est v= 1 m/s.
  ----> aide :
  entre A et M il y a 1 m ; la perturbation atteint M, 0,1 s après A
  v= AM / 0,1 = 1/0,1 =10 m/s.
3. La date t1 vaut 0,5 s
4. La durée de la perturbation ( durée pendant laquelle un point de la corde est en mouvement) est 0,03 s.
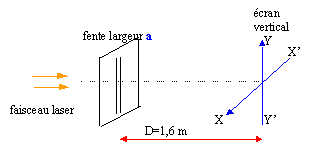
On mesure sur l'écran la largeur d de la tache centrale de diffraction pour plusieurs valeurs de la largeur a de la fente. La précision de la mesure de la largeur d est 0,5 mm.
a (mm) 0,5 0,25 0,2 0,1
d(mm) 6,5 13 16 32
aide : produit ad (mm²) 3,25 3,25 3,2 3,2
1. La figure de diffraction présente des taches qui s'étalent suivant l'axe Y'Y de l'écran.
2. l'écart angulaire de la demi tache centrale de diffraction est donnée par :
  longueur d'onde / largeur fente
3. La largeur de la tache centrale est inversement proportionnelle à a
  ----> aide : le produit ad est constant
4. Pour la largeur a= 0,2 mm, l'angle sous lequel la tache centrale est vue de la fente est 0,01 rad
  ----> aide :
  d / D= 1,6 10^ -2 / 1,6 = 0,01 rad
Le césium 137 est un élément radioactif béta -. La demi vie t½ du césium 137 est 30 ans. On donne : Te (Z=52) ; I( Z= 53) ; Xe ( Z= 54) ; Cs(Z=55) et Ba ( Z=56)
1. L'équation (1) correspond à la désintégration du noyau de césium 137
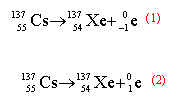
2. Le noyau fils peut se mettre dans un état excité et émettre un rayonnement gamma.
3. La constante radioactive vaut 0,023 an-1.
  ----> aide :
  constante radioactive * t½= ln2 = 0,7
  avec t½=30 ans.
4. La durée nécessaire à la disparition de 99% de césium est environ 200 ans.
  ----> aide :
  à chaque demi vie la moitié des noyaux de césium initiaux diqparaît
  à t½=30 ans, 50% disparu
  à 2t½=60 ans, 75% disparu
  à 3t½ = 90 ans, 87,5 % disparu
  à 4t½, 93,7 % disparu.......
On considère la réaction suivante :
1. Il s'agit d'une désintégration spontanée
2. Le nombre de neutrons formés est x=3
  ----> aide : conservation du nombre de nucléons :
  235+1= 135+97+3x
3. L'élément Yttrium, symnole Y a pour numéro atomique 39
  ----> aide :
  conservation de la charge :
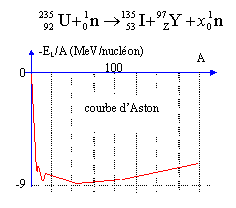
  92 = 53+Z
4. D'après la courbe d'Aston, l'énergie libérée par la réaction est inférieure à 10 MeV.
  ----> aide :
  uranium 235 : -7,6 MeV par nucléon et 235 nucléons soit -7,6*235 = - 1786 MeV
  pour les noyaux fils : environ -8,6 Mev et 232 nucléons soit - 1995 MeV
  différence proche de 200 MeV
On dispose d'un échantillon de matière radioactif.
1. L'activité A(t ) d'une source radioactive, avec les notations habituelles, a pour expression : A(t) = No exp ( - lambda t)
2. L'expression " le radium est plus radioactif que l'uranium " signifie que le nombre de noyaux radioactifs de radium diminue plus rapidement au cours du temps que le nombre de noyaux radioactifs d'uranium.
  ----> aide :
  activité = lambda N = -dN / dt
3. Au bout de trois demi vie, les 3/4 des atomes radioactifs se sont désintégrés.
  ----> aide :
  à chaque demi vie la moitié des atomes initiaux se désintègrent.
  à t½, 50% désintégrés
  à 2t½ : 50% + 25% désintégrés
4. Le noyau stable de plomb 206 ( Z= 82) est obtenu à partir de désintégrations successives alpha et béta - du noyaux de radium 226 ( Z= 88). 5 particules alpha et 10 électrons sont émis
  ----> aide :
  béta - : A inchangé et Z augmente de une unité
  alpha : A diminue de 4 unités et Z diminue de 2 unités
  donc 226-206 = 20 soit 5 désintégrations alpha
  82-88 = -6 soit -5*2 + x= -6 soit 4 électrons émis
La charge d'un condensateur de capacité C est réalisée en brabchant en série un conducteur ohmique de résistance R et un générateur de tension idéale de fem E. Le condensateur est initialement déchargé et à la date t=0 on ferme l'interrupteur K.
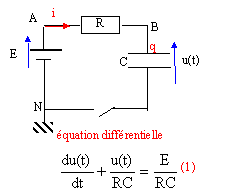
1. La solution de l'équation différentielle est u(t) = E ( 1- exp (- t/ constante de temps))
2. La charge finale du condensateur est de l'ordre de E/C
3. La méthode d'Euler permet de calculer u(t) par itérations successives avec l'expression suivante : u(t+ dt) = u(t) + du(t). On peut alors écrire : u(t+dt) = u(t) + (E-u(t)) dt
4. par la méthode d'Euler, plus le pas est grand, plus u(t) se rapproche de la solution de l'équation différentielle
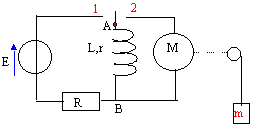
Le moteur est lié mécaniquement à une poulie à laquelle est suspendue une masse m= 10 g. Lorsque le moteur fonctionne il remonte la masse m
E= 12,5 V ; R= 40 ohms ; r= 10 ohms ; L= 1 H ; g= 10 m/s².
1. Interrupteur en position 1 :
  en régime permanent l'intensité du courant vaut I= 0,31 A
  ----> aide :
  I= E/(R+r) soit 12,5 / 50 = 0,25 A
2. Interrupteur en position 1 :
  l'énergie électromagnétique emmagasinée dans la bobine est 31 mJ
  ----> aide : ½LI² avec I= 0,25 A et L= 1 H
3. Interrupteur en position 2 :
  le courant circule de B vers A dans la bobine
4. Interrupteur en position 2 :
  si les frottements sont négligeables, la masse monte de h= 31 cm
  ----> aide
  l'énergie électromagnétique stockée (31 mJ) est convertie en énergie potentielle de pesanteur
  31 = mgh avec m = 10 et g= 10.
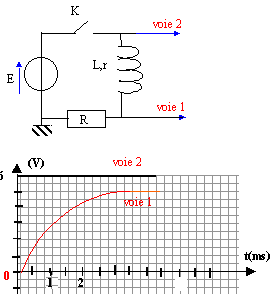
R= 50 ohms ; E= 6 V.
On ferme l'interrupteur à t=0.
1. La bobine s'oppose aux variations de la tension dans le circuit
2. En régime permanent, l'intensité du courant vaut 100 mA
  ----> aide :
  sur la voie 1 on visualise la tension aux bornes du résistor
  5= 50 I en régime permanent
3. La résistance r de la bobine vaut 60 ohms.
  ----> aide :
  en régime permanent la tension aux bornes de la bobine vaut 1 V
  1 = rI= r*0,1 soit r=10 ohms
4. L'inductance de la bobine vaut environ L= 60 mH.
  ----> aide :
  déterminer graphiquement la constante de temps à partir du graphe voie 1 ( la tangente à l'origine coupe l'asymptote à 5 V vers t= 1 ms)
  constante de temps = L/( R+r) = 0,001
  soit L= 0,001*(50+10) = 60 mH
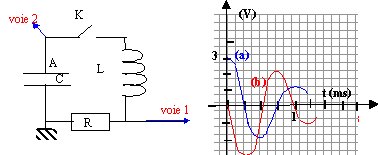
C= 10 microfarads.
Le condensateur est initialement chargé et son armature A porte une charge Qo= + 30 microcoulombs. A l'instant t=0 on ferme l'interrupteur K et on visualise la tension aux bornes du condensateur et de la résistance.
1. A t=0 la tension aux bornes du condensateur est environ 3V
2. La courbe a représente la tension aux bornes du condensateur
3. La courbe b est proportionnelle à l'énergie stockée dans le circuit
  ----> aide :
  l'énergie peut être stockée par le condensateur et par la bobine inductive
4. La valeur de l'inductance est proche de 2,5 mH.
  ----> aide :
  La pseudopériode est voisne de 10^ -3 s (lecture graphe)
  Cette valeur est voisine de la période propre du dipôle LC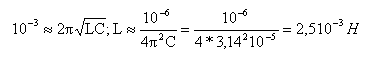
Une balle de volume V et de masse m tombe verticalement dans l'air.

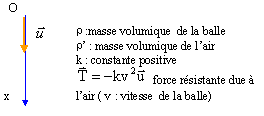
----> aide :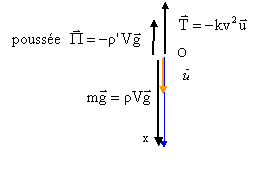
1. La deuxième loi de Newton peut s'écrire :
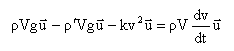
2. l'équation différentielle du mouvement s'écrit :
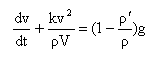
3. La vitesse a pour valeur limite :
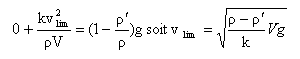
4. Une fois la vitesse limite atteinte, l'accélération de la bille est une constante non nulle
Une balle supposée ponctuelle de masse m= 200 g est lancée d'un point A situé à la distance h du point O du sol avec une vitesse initiale horizontale Va=4 m/s. La balle n'est soumise qu'à son poids. g= 10 m/s². La balle touche le sol à la distance d= 4 m du point O.
----> aide :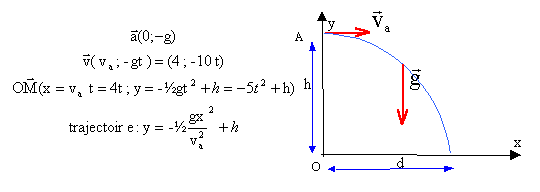
1. Dans le repère (O,i , j) l'équation de la trajectoire s'écrit : y= -½gx²/ ( 2Va²) +h
2. La durée de la chute est 1s.
  ----> aide :
  au sol x= 4 = 4t soit t= 1s
3. La hauteur h a pour valeur 5 m
  ----> aide :
  au sol y=0 et t= 1s.
  h= ½gt² = 0,5*10*1² = 5 m
4. La vitesse d'arrivée au sol de la balle peut s'écrire :
  V²s= V²a + 2gh
  ----> aide :
  seul le poids travaille ; le travail est moteur et vaut mgh
  le théorème de l'énergie cinétique s'écrit :
  ½mV²s-½mV²a= mgh.
Un oscillateur mécanique non amorti est constitué d'un ressort de raideur k= 6 N/m dont l'une des extrémité est reliée à un objet ponctuel A de masse m=60 g pouvant glisser sans frottement le long d'une tige horizontale.
A la date t=0, l'objet est écarté de sa position d'équilibre O d'une distance Xo= - 4cm et laché sans vitesse initiale.
----> aide :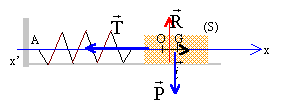
1. La force de rappel et l'abscisse x sont toujours de sens contraire.
2. La dérivée de l'énergie mécanique totale du système ( solide ressort) s'écrit :
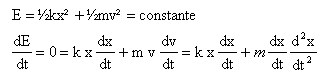
3. La pulsation du mouvement a pour valeur 10 rad/s
  ---->aide :
  pulsation ² = k/m = 6/ 0,06 = 100
4. La position du centre d'inertie de la masse est donnée à chaque instant par :
  x(t) = 0,04 cos (10 t)
Un satellite artificiel de masse m=2,5 tonnes gravite autour de la terre à une altitude constante h= 270 km. La terre est considérée comme ayant une répartition de masse à symétrie sphérique.
masse de la terre : M= 6 10^ 24 kg ; rayon de la terre : R= 6,4 10^ 3 km ; constante de gravitation G= 6,67 10^ -11 SI
1. Le satellite est en orbite circulaire dans le référentiel héliocentrique
2. Le vecteur accélération du satellite est orthogonal à son orbite
3. La 3ème loi de kepler a pour expression :
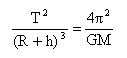
4. Dans le référentiel géocentrique la vitesse du satellite est environ 7,7 km/h
  ----> aide :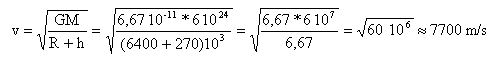
Une masse m=200 g accrochée à l'extrémité d'un pendule simple de longueur L=1 m et on lui communique une vitesse horizontale Vo= 3 m/s à partir de sa position verticale.g= 10m/s² ; pi²= 10
1. La longueur d'un pendule simple qui bat la seconde ( ou de période 2s) est de 1m
2. Lorsque l'élongation angulaire est maximale,( notée a), l'énergie mécanique du système ( pendule terre) est E= mgL( 1- sin a)
  ---->aide :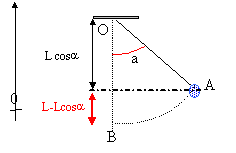
3. L'amplitude angulaire est proche de 60°
  ----> aide :
  ½mVo²= mgL(1-cos a)
  1-cos a= Vo²/(2gL) ;
  cos a = 1-Vo²/(2gL)
  cos a = 1-9/20 = 0,55
  amplitude angulaire proche de 60°
4. Quand le pendule passe par la verticale, la tension du fil a pour valeur 2N
  ----> aide :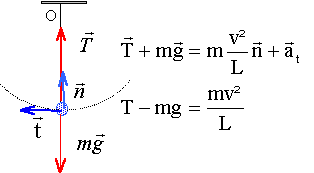
  
  T= mg + mVo²/L
  T= 0,2*10 + 0,2*9 = 3,8 N
Pour chauffer des aliments dans un micro-ondes, on excite, par absorption, les molécules d'eau qu'ils contiennent. L'émetteur est un oscillateur qui émet des ondes électromagnétiques dont l'énergie est de 10^ -5 eV. e= 1,6 10^ -19 C ; h= 6,62 10^ -34 Js.
1. Le phénomène mis en jeu est un phénomène de résonance
2. La fréquence propre de l'oscillateur est de l'ordre de 10^ 16 Hz
  ----> aide :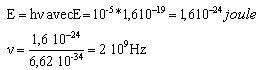
3. L'oscillateur émet dans l'ultra-violet
4. Les transitions mises en jeu sont des transitions atomiques

a (mm)	0,5	0,25	0,2	0,1
d(mm)	6,5	13	16	32
aide : produit ad (mm²)	3,25	3,25	3,2	3,2