Aurélie jan 04

Kiné Ceerrf d'après concours 2004 sans calculatrice

force de Laplace -le motard - optique : les lentilles- chimie

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


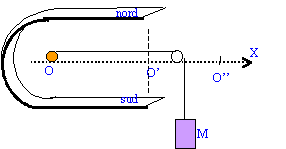
On considère un conducteur mobile cylindrique de longueur L=8 cm et de masse m= 8g, posé sur des rails conducteurs, écartés d'une longueur l= 6 cm. Les rails sont reliès aux bornes d'un générateur de courant continu d'intensité I= 6 A. Le circuit est soumis au champ magnétique uniforme de valeur B= 0,1 T. On néglige les frottements.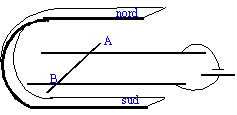

  1. Reproduire le schéma en indiquant le sens du champ magnétique.
  2. Déterminer le sens et la direction de la force de Laplace qui s'exerce sur le conducteur mobile AB.
  3. A l'aide d'un fil inextensible enroulé, de masse négligeable, et d'une poulie, on attache une masse M au conducteur AB. Quelle doit être la valeur de M pour que le conducteur AB soit en équilibre ?
  4. On enlève le fil et la masse M, puis on permutte les bornes du générateur. On considère que le conducteur mobile est initialement au repos en O et est soumis au champ magnétique sur la longueur OO' = 4 cm
    - Déterminer la nature du mouvement du conducteur AB sur la longueur OO' ( sans application numérique)
    - Exprimer littéralement puis numériquement l'équation horaire v(t) de ce mouvement
    - Exprimer littéralement puis numériquement l'équation horaire x(t) de ce mouvement
    - Calculer la vitesse du conducteur mobile en O'.
    - Combien de temps met le conducteur AB pour aller de O à O" sachant que d'=O'O" = 10 cm

données : g= 10 m/s² ; L= 8 cm ; I= 6 A ; B= 0,1 T ; m= 8 g ; l=6 cm

 

corrigé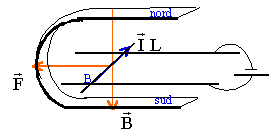

AB est soumis à son poids opposé aux action des rails

à la force de laplace F et à la tension du fil T= Mg

à l'équilibre F=T soit B I AB = Mg soit M= B I AB / g= 0,1*6*0,06 / 10 = 3,6 10-3 kg = 3,6 g.

mouvement uniformément accéléré entre O et O'.

Le poids et l'action des supports sont opposés ; la force de Laplace change de sens si on permutte les bornes du générateur

écrire la seconde loi de Newton suvant l'axe OX : B I AB = m x"

x"= B I AB / m = 0,1*6*0,06/ 0,008 = 6/8 = 4,5 m/s².

par intégration on trouve la vitesse ( la vitesse initiale est nulle, donc la constante d'intégration est nulle)

v(t)= 4,5 t

par intégration on trouve la position x : x(t) = 2,25 t²

en combinant ces deux relation on peut écrire : v²= 9 x

vitesse en O' : racine carrée (9*0,04)= 0,6 m/s.

entre O' et O" la tige AB est pseudoisolée et le mouvement est rectiligne uniforme.

O'O"= 0,6 t soit t = 0,1/0,6 =0,17 s.

durée du parcours OO' : 0,04 = 2,25 t² soit t = racine carrée(0,04/2,25) = 0,13 s

durée du parcours OO" : 0,13 + 0,17 = 0,3 s.


Un motard roule sur une côte inclinée. Au sommet le centre d'inertie du motard passe en O avec une vitesse v0 faisant un angle a =30° avec l'axe des abscisses, ce qui permet d'effectuer un saut au dessus d'un plan incliné d'un angle b =45° par rapport à l'horizontale.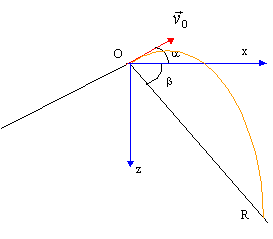

  1. Etablir littéralement les équations horaires x(t) et z(t) correspondant au saut :
    - par calculs
    - sans calculs en utilissant les formules du cours.
  2. Etablir littéralement l'équation de la trajectoire et conclure.
  3. Déterminer littéralement les coordonnées xR et zR du point de réception R.
  4. Calculer numériquement les coordonnées xR et zR
  5. Etablir littéralement la durée du saut tR.
  6. Calculer tR.
  7. Au cours du saut le motard passera-t-il plus de temps "au dessus de l'horizontale" ou " sous l'horizontale" ? Justifier par un calcul.

sin 45 = cos 45 ; sin²45 = 0,5 ; v0= 36 km/h ; sin 60 = 0,87 ; g= 10 m/s² ; masse motard et moto = m = 180 kg.

 

corrigé
vecteur accélération ( 0,g)

vecteur vitesse initiale : (v0 cos a ; -v0 sina)

vecteur vitesse primitive de l'accélération ( v0 cos a ; gt - v0 sina)

vecteur position primitive du vecteur vitesse

x = v0 cos a t ; z = ½gt² - v0 sina t

en éliminant le temps on trouve la trajectoire z = ½g x² / (v0 cos a)² - x tan a.

au point d'impact R : xR = zR car b =45° (équation de la droite OR : z = x)

repport dans l'expression donnant la trajectoire :

xR = zR = ½g xR ² / (v0 cos a)² - xR tan a.

simplifier par xR : 1= ½g xR / (v0 cos a)² - tan a.

xR = zR = 2(1+tan a )(v0 cos a)² / g

tan 30 = 0,577 ; cos²30 = 0,75 ; v0 = 10 m/s ; g= 10 m/s²

xR = zR =2(1+0,577)*100*0,75 /10 = 23,65 m.

durée du saut : xR = v0 cos a tR donne tR = xR /( v0 cos a)= 23,65/(10*0,866)= 2,73 s.

temps passé au dessus du plan horizontal : écrire que z = 0

0= ½gt² - v0 sina t ; ½gt - v0 sina =0 soit t= 2 v0 sina /g= 2*10*0,5/10= 1 s.

temps passé sous l'horizontale: 2,73-1 = 1,73 s.

A.N : avec a = 60°.

tan 60 = 1,73 ; cos²60 = 0,25 ; v0 = 10 m/s ; g= 10 m/s²

xR = zR =2(1+1,73)*100*0,25 /10 = 13,6 m.

durée du saut : xR = v0 cos a tR donne tR = xR /( v0 cos a)= 13,65/(10*0,5)= 2,73 s.

temps passé au dessus du plan horizontal : écrire que z = 0

0= ½gt² - v0 sina t ; ½gt - v0 sina =0 soit t= 2 v0 sina /g= 2*10*0,866/10= 1,73 s.

temps passé sous l'horizontale: 2,73-1,73 = 1 s.

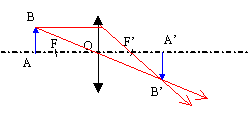
On considère deux lentilles minces convergentes L1 et L2 de distance focale f'1=5 cm et f'2 = 5 cm de centre optique O1 et O2.

  1. On accole les deux lentilles. Etablir l'expression de la vergence v de la lentille unique L équivalent aux deux lentilles accolées en fonction des distances focales.
  2. Calculer numériquement la vergence v puis la distance focale f' de L.
  3. Déduire des questions précédents la valeur de la distance focale f" de la lentille unique L' équivalent à 4 lentilles L1 accolées.
  4. L'objectif d'un appareil photographique est assimilé à une lentille L2 dont le diamètre d'ouverture est limité à 1 cm par un diaphragme circulaire accolé à L2. La pellicule P est située à 7,5 cm de O2.

    - A quelle distance de L2 doit-on placer un objet A, ponctuel, situé sur l'axe optique pour que son image A' se forme sur la pellicule ?
    - Faire le schéma de principe de la formation de A' à partir de 2 rayons issus de A.
    - On approche A de L2 : sans calculs, montrer dans quel sens A' s'éloigne de la pellicule.
    - On estime que la tache lumineuse sur la pellicule ne doit pas dépasser 2 micromètres pour obtenir une photographie nette. On approche A de L2 (objectif) : à partir de quelle position A1 l'image n'est-elle plus nette ? On notera A'1 l'image de A1 et on considère que la distance A'A'1 est très petite devant la distance A'1O2( schéma souhaité)

données : 7,5015 -1 = 0,133 ; 0,067 -1 = 14,925

corrigé
la vergence des deux lentilles accolées est égale à la somme des vergence de chaque lentille.

la vergence en dioptrie est l'inverse de la distance focale exprimée en mètre

v = 1/f'1 + 1/f'2 = 1/ 0,05+1/0,05 = 40 d.

distance focale de cette lentille : f' = 1/40 = 0,025m = 2,5 cm.

lentille équivalente à 4 lentilles L1 accolées : vergence 4*20=80 d et distance focale 1/80 = 1,25 cm.

ce qui est écrit en gras et en bleu est une mesure algébrique.

1/f'2 = 1/ O2A' - 1/ O2A ; 1/ O2A =1/ O2A' -1/f'2.

1/ O2A =1/ 0,075-1/0,05 = -6,667 doù O2A = -0,15 m.

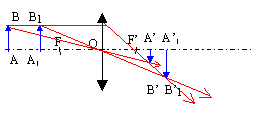
en approchant A de la lentille ( en restant en dehors de FO) l'image s'éloigne de la pellicule vers la droite

on pose : AO-A1O= Dx ; A'1B'1 -A'B' = 2 10-6 m

diamètre apparent de l'image A'B': A'B'/OA'

diamètre apparent de l'image A'1B'1: A'1B'1 /OA'1 voisin A'1B'1 /OA'

différence : 210-6 / OA' = 2 10-6 / 7,5 10-2 = 2,67 10-5 rad

diamètre apparent de l'objet AB : AB/OA

diamètre apparent de l'objet A1B1: A1B1 /OA1= AB/OA1

différence : AB(1/OA1- 1/OA) = 2,67 10-5

AB(OA-OA1) / (OA*OA1)=2,67 10-5

or OA proche OA1 d'où : AB Dx / OA² = 2,67 10-5

AB Dx = 2,67 10-5 OA² = 2,67 10-5 *0,15² = 6 10-7 m

si AB = 0,1 mm = 10-4 m , alors Dx = 6 10-3 m.

 

  1. L'acide éthanoïque réagit avec l'éthanol pour donner un composé inconnu X et de l'eau. Nommer cette réaction et la réaction inverse.
  2. Ecrire l'équation bilan et nommer le composé X.
  3. On mélange 120 g d'acide éthanoïque, 92 g d'éthanol et 54 g d'eau.
    - A l'aide d'un tableau d'avancement , déterminer la valeur de la constante d'équilibre de cette réaction
    - Dans quel sens la réaction du mélange se déplace-t-elle ? Justifier.
    - Déterminer la composition du mélange à l'équilibre.
  4. Vers quel état d'équilibre évoluerait un mélange de 1 mole de X, 1 mole d'acide, 1 mol d'alcool et 1 mole d'eau. Justifier l'évolution du système.

C=12 ; H=1 ; O=16 g/mol. 0,67/2 = 0,33 et 0,75/2 = 0,38

 

corrigé
acide éthanoïque + éthanol = éthanoate d'éthyle + eau

estérification ; la réaction inverse est l'hydrolyse de l'ester

CH3-COOH + CH3-CH2-OH = CH3-COO-CH2-CH3 + H2O

Quantité de matière (mol) = masse (g) / masse molaire (g/mol)

acide éthanoïque : 120 / 60 = 2 mol

alcool éthylique : 92 / 46 = 2 mol

eau : 54/18 = 3 mol

CH3-COOH
+ CH3-CH2-OH
= CH3-COO-CH2-CH3
+ H2O
initial
2 mol
2
0
3
en cours
2-x
2-x
x
3+x
équilibre
2-xéq
2-xéq
xéq
3+xéq
si on part d'un mélange équimolaire en alcool primaire et en acide, à l'équilibre on obtient 66,6% d'ester

K= 0,666 *0,666 /(1-0,666)² = 4

or dans le mélange précédent Qr,i = [CH3-COO-CH2-CH3][ H2O] /([CH3-CH2-OH][CH3-COOH])=0 ; il n'y a pas d'ester au départ

Qr,i < K donc évolution spontanée vers la droite, sens direct.

Qr,éq= K = 4 = xéq(3+xéq) /(2-xéq)²

4(2-xéq)² = xéq(3+xéq)

4x²éq +16 - 16xéq = 3 xéq + x²éq.

3x²éq - 19xéq +16 =0

solutions : 5,33 et 1

xéq ne peut être supérieur à 2 mol donc xéq = 1 mol.

à l'équilibre : 1 mol d'acide, 1 mol d'alcool, 1 mol d'ester et 4 mol d'eau.

à partir du mélange : 1 mol d'acide, 1 mol d'alcool, 1 mol d'ester et 1 mol d'eau Qr,i =1 ;

Qr,i < K donc évolution spontanée vers la droite, sens direct.


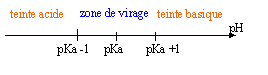
A- Un indicateur coloré est un couple acide base. Les deux espèces conjuguées sont de teintes différentes. On note ce couple Hind / ind-, constante d'équilibre Ka.

  1. Ecrire l'équation bilan de la réaction de la forme acide avec l'eau
  2. Etablir l'expression du pH en fonction du pKa et des concentrations des espèces Hind et ind-.
  3. Pour que la teinte de l'une des deux espèces conjuguées ( acide ou base) occulte complétement l'autre il faut un rapport de concentration au moins égal à 10. Quelle doit être le pH de la solution, par rapport au pka pour que l'on obtienne la teinte acide ?
    - Quelle doit être le pH de la solution, par rapport au pka pour que l'on obtienne la teinte basique ?
    - Sur une échelle de pH représenter les domaines de la teinte acide, de la teinte basique, de la teinte sensible.

B- On réalise la combustion complète dans l'air d'un composé oxygéné Z de formule CnH2nO. En faisant réagir 72 g de Z on obtient 176 g de CO2.

  1. Donner l'équation de la réaction de combustion en fonction de n.
  2. Déterminer la quantité de matière de dioxyde de carbone formé.
  3. Exprimer en fonction de n la quantité de matière du composé Z que l'on fait réagir.
  4. Ecrire le tableau d'avancement en fonction de n.
    - En déduire la valeur de n.
    - Réécrire l'équation de la réaction en remplaçant n par sa valeur.

     

corrigé
Hind + H2O = ind- + H3O+. Ka = [ ind- ][H3O+] / [Hind ]

log Ka = log [H3O+] + log ([ ind- ] / [Hind ])

- log [H3O+] = -log Ka + log ([ ind- ] / [Hind ])

pH=pKa++ log ([ ind- ] / [Hind ])

teinte basique alors [ ind- ] / [Hind ] =10

pH = pKa + log 10 = pKa+1

teinte acide alors [ ind- ] / [Hind ] =0,1

pH = pKa + log 0,1 = pKa-1

CnH2nO + (1,5 n-0,5)O2 = nCO2 + nH2O

Qté de matière CO2 (g) = masse (g) / masse molaire (g/mol) = 176/44 = 4 mol

Qté de matière du composé Z : 72 / (12n+2n+16) = 72/(14n+16)

CnH2nO
+ (1,5 n-0,5)O2
= nCO2
+ nH2O
initial
72/(14n+16)
en excès

(combustion complète)
0
0
en cours
72/(14n+16)-x
n x
n x
fin
72/(14n+16)-xmax=0
n xmax = 4
n xmax

72/(14n+16)-xmax=0 donne xmax=72/(14n+16)

n xmax = 4 donne xmax = 4/n

d'où : 4/n = 72/(14n+16) soit 72 n = 4(14n+16)

72 n = 56 n+64 ; 16n=64 soit n=4.

C4H8O + 5,5O2 = 4CO2 + 4H2O

retour -menu