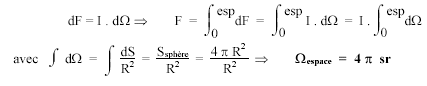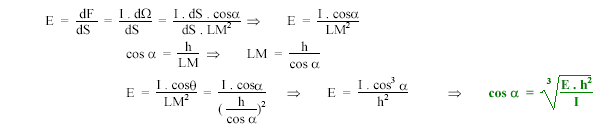piscine - capteur solaire - éclairage

d'après BTS travaux publics

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


piscine

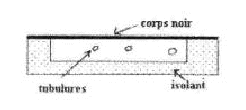
Une piscine rectangulaire mesure 20 m de long, 10 m de large et une profondeur de 3 m.

  1. Calculer la quantité de chaleur mise en jeu, lorsque la température de l'eau de la piscine varie de 1°C.
  2. Pendant le jour, l'eau se réchauffe grâce au rayonnement solaire. L'eau reçoit une puissance moyenne P1= 300 W /m², pendant une journée de 12 h. L'eau n'absorbe en fait que 50 % de cette puissance.
    - Calculer l'énergie Q1 absorbée par l'eau pendant ces 12 h.
    - Calculer pour cette eau, l'augmentation de température Dq1 qui en résulte.
  3. Pendant la nuit l'eau de la piscine rayonne de l'énergie vers l'atmosphère. On considère que l'eau se comporte comme un corps noir ; on admet que sa température est q =25°C.
    - Calculer la puissance P2 perdue par rayonnement par cette eau par m² de surface.
    - Calculer l'énergie thermique Q2 perdue au cours de 12 h de nuit.
    - Calculer pour cette eau, la baisse de température Dq2 qui en résulte.
    - par quel dispositif simple peut-on la nuit, diminuer la perte par rayonnement ?
  4. Faire le bilan énergétique sur une journée de 24 h.
  5. Pour exploiter la piscine à moindre coût, on peut utiliser un chauffage solaire de l'eau. On réalise des capteurs solaires dans lesquels circule l'eau de la piscine. Les capteurs utilisent l'effet de serre. Expliquer à l'aide d'un schéma le principe de fonctionnement de ces capteurs.
    capacité thermique massique de l'eau : ceau = 4180 J kg-1 K-1 ;
    loi de Stéphan P=sT4 ou P s'exprime en Wm-2 ; s= 5,67 10-8 Wm-2K-4.
corrigé
Q= m ceau (qf-q1) avec m (kg)= r (kg m-3) V (m3) ; V= 20*10*3 = 600 m3.

m = 1000*600 =6 105 kg ; Q= 6 105* 4180 *1 = 2,51 109 J.

Puissance totale : P = P1 . S avec S = L . l = 200 m2

P= 300*200 =6 104 W

l'eau ne reçoit que 50% de cette puissance soit : 3 104 W

énergie reçue par l'eau en 12 h = 12*3600 = 4,32 104 s.

Q1 = 3 104*4,32 104 = 1,3 .109 J.

augmentation de température Dq1 =Q1/(m ceau )= 1,3 109/(4180*6 105)=0,51°C.

puissance perdue par rayonnement nocturne par m²:

P2=sT4 ; s= 5,67 10-8 Wm-2K-4 ; T=273+25=298 K

P2=5,67 10-8 *2984=447,1 Wm-2.

puissance perdue par la surface de l'eau : 447,1*200 = 8,94 104 W

énergie perdue en 12 heures (4,32 104 s) : Q2 = 8,94 104*4,32 104 = 3,86 109 J.

baisse de température Dq2 =Q2/(m ceau )= 3,86 109/(4180*6 105)=1,54°C.

On peut couvrir la piscine.

Qtot = Q1 - Q2 = – 2,56.109 J

On fait circuler l'eau dans des canalisations en serpentin, placées sous une vitre et sur un fond noir.


capteur solaire

 

loi de Stéphan P=sT4 ou P s'exprime en Wm-2 ; s= 5,67 10-8 Wm-2K-4.

et lmaxi .T = 2,9.10-3 m.K (loi de Wien)

On utilise un capteur solaire pour réchauffer l'eau soutirée du puits. Ce capteur plan sera considéré comme un corps noir (radiateur intégral). Il reçoit du soleil un flux énergétique par mètre carré de 1000 W.m–2

  1. Calculer la température d'équilibre du capteur (exprimée en Kelvin puis en degré Celsius).
  2. Calculer la longueur d'onde où le capteur émet le plus d'énergie.
  3. Quel est le nom donné au rayonnement ayant cette longueur d'onde ?
corrigé
Quand il sera à l'équilibre, l'énergie qu'il reçoit sera égale à l'énergie qu'il rayonne.

Energie reçue par m2 : E1 = 1000 W.m-2 ;

Energie rayonnée : E2 = sT4

T4 = 1000 / 5,67 10-8 =1,76 1010.

T= 364 K soit 364-273 = 91 °C.

La loi de Wien donne la longueur d’onde où se situe le maximum d’émission :

lmaxi .T = 2,9.10-3 ; lmaxi = 2,9.10-3 / 364 = 7,97 10-6 m = 7970 nm

Le domaine visible va de 400 nm (violet) à 800 nm (rouge)

lmaxi > 800 nm : le rayonnement est situé dans l’INFRA-ROUGE

éclairage

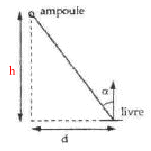
Les questions 3 et 4 sont indépendantes des questions 1 et 2.

Une ampoule électrique de flux lumineux F rayonne uniformément dans toutes les directions. Elle se trouve à la hauteur h au-dessus d'un plan contenant une table. Une personne lit un livre posé sur cette table. L'éclairement en un point du livre situé à la distance d de la verticale passant par l'ampoule est E0. L'angle entre les rayons lumineux et la verticale est noté a.

Données: F = 1500 lm. h = 1,5 m. E0 = 25 lux.

  1. Démontrer que le flux lumineux total émis par l'ampoule a pour expression, F = 4p.I, I étant l'intensité lumineuse de l'ampoule. Application numérique : calculer I.
  2. Démontrer que : cos a = racine cubique( E . h2/I). Application numérique : calculer d.
  3. L'éclairement de la page du livre peut être considéré comme uniforme. Son pouvoir absorbant est 0,8. Calculer son exitance.
  4. Calculer la luminance de cette page sachant qu'elle suit la loi de Lambert

 

corrigé

Donc F = 4 p I soit I = 1500/(4*3,14)=119,4 cd.

Application numérique : cos3 a = E h² / I= 25* 1,5² /119,4=0,471 ; cos a = 0,778 ; a = 39°

Calcul de d : tan a = d/h d'où d= h tan a = 1,5 tan 39 = 1,21 m.

Pouvoir absorbant = 0,8. ; pouvoir réflecteur r = 1 – 0,8 = 0,2 (20%)

D’où son exitance : M = r . E = 0,2 * 25 = 5 W.m–2 .

Source qui suit la loi de Lambert : I = Cte dans toutes les directions

Luminance : L = I / (pR²)

Exitance : M = P/ (4pR²) surface de la sphère

Comme F = 4 p I ; M = 4 p . I

ce qui donne : L = M /p

L = 5/3,14 = 1,6 cd.m–2.



retour -menu