étude d'un judas - propriètés du laser

d'après BTS génie optique 03

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


étude d'un judas

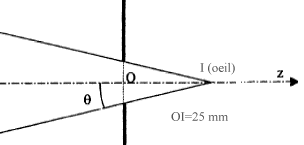
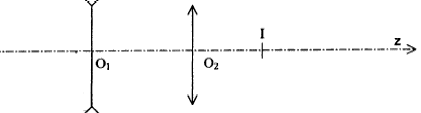
Un judas est une petite ouverture munie d'une lentille traversant la porte et permettant de voir de l'intérieur vers l'extérieur.

Questions préliminaires :

  1. La solution la plus simple pour observer à l'extérieur d'une porte est de pratiquer un trou circulaire dans la porte. Le diamètre du trou est D= 10 mm et le centre du trou est à 1,6 m du sol.

    - Quelle est la valeur de q ?
    - Une personne est à 50 cm devant la porte; quelle doit àtre la valeur minimale hm de sa taille pour quelle soit partiellement visible par l'oeil placé en I ?

  2. Utilisation d'une lentille mince divergente : pour augmenter le champ de vision, on place dans le trou une lentille mince divergente notée L0, de vergence C0= -1 d. Le centre optique de cette lentille est confondu avec le centre du trou et son axe optique est Oz. L'oeil placé en I observe à travers la lentille un objet AB.

    - Déterminer par le calcul les caractèristiques de l'image A'B' donnée de AB par la lentille ( OA= - 0,5 m ; AB= 0,1 m) les mesures algèbriques sont écrites en bleu et en gras.
    - Calculer l'angle a' sous lequel l'oeil voit l'image A'B'.
    - Calculer l'angle a sous lequel l'oeil voit l'objet AB en absence de lentille.
    - Calculer le grossissement du système optique que constitue la lentille.

  3. Etude du système optique réel : Le judas est en fait constitué d'une lentille convergente ( vergence C2) et d'une lentille divergente (vergence C1= -20 d ). Ces deux lentilles sont minces. La vergence C du système complet est C= -1 d. Les centres optiques des deux lentilles sont notés O1 et O2 et O1O2 = e = 30 mm. L'oeil est toujours placé en I avec O2I= 25 mm.

    - Calculer la valeur de la vergence C2.
    - Déterminer les positions H et H' points principaux de ce système. On donnera les valeurs de O1H et de O2H'.
    - On place un objet de très petite taille au point A de l'axe optique tel que O1A= -50 cm. l'image donnée par le système optique réel, de l'objet placé en A se forme en A'. Déterminer sa position en calculant la valeur H'A', puis celle de IA'.

  4. Détermination du champ du système optique : on utilise le système de deux lentilles précédent. Les diamètres D1 et D2 des deux lentilles sont égaux à celui du trou dans la porte soit 10 mm. On utilisera les valeurs f '1= -50 mm ; f '2= 84,2 mm et O1O2=e=30 mm.
    - L'oeil observe un objet AB dont la position est donnée par O1A= -50 cm. Dans cette situation quel élément est d'aphragme d'ouverture ?
    - Déterminer les positions et dimensions de la pupille d'entrée et de la lucarne d'entrée.
    - Déterminer les dimensions du champ total objet. On illustrera le raisonnement par un schéma.
    - Déterminer la taille minimale h'm que doit avoir une personne pour être partiellement visible. Comparer au résultat obtenu avec une seule lentille et conclure.

corrigé
tanq= 5/25 = 0,2 soit q =11,3° ou 0,2 rad.

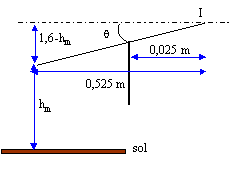
taille minimale hm : tanq= (1,6-hm)/0,525 = 0,2 ; 1,6-hm=0,2*0,525=0,105 ; hm= 1,495 m.

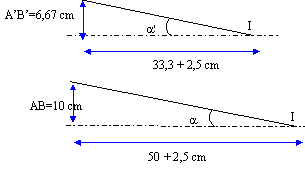
formule de conjugaison : 1/f'=1/OA'-1/OA soit 1/OA' = 1/f'+1/OA avec 1/f'= -1 et OA =-0,5 m

1/OA' = -1 +1/(-0,5) = -3 ; OA' = -0,333 m

donc l'image est à gauche de la lentille, image virtuelle

grandissement : g = OA' / OA= -0,333 / (-0,5) = 0,667 donc l'image est droite

taille A'B' = g AB= 0,667 * 10 = 6,67 cm.

tan a' = 6,67 / 35,8 = 0,187 ; a '= 10,6° ou 0,187 rad.

tan a = 10 / 52,5 = 0,19 ; a '= 10,8° ou 0,19 rad.

grossissement G= a '/a= 0,98.

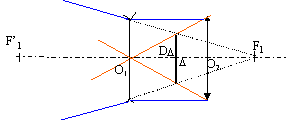
C=C1+C2-eC1C2 soit -1 = -20 + C2- 0,03(-20)C2 ; C2 = 11,87 d.

plans principaux: plans conjugués pour lesquels le grandissement transversal g vaut 1.

O1H= eC2/C = 0,03*11,87/(-1) = -0,356 m.

O2H'= -eC1/C = -0,03*(-20)/(-1) = -0,6 m.

la relation de conjugaison s'écrit : 1/f'=C= 1/H'A'-1/HA

1/H'A'= C+1/HA avec HA = H O1 +O1A= 0,356 +(-0,5) = -0,144.

1/H'A'= -1+1/(-0,144) = -1-6,94 soit H'A'= -0,126 m.

IA' = IO2+ O2H'+H'A'= -0,025 +(-0,6)+(-0,126) = -0,751 m.

soit D le conjugué objet de O2 relativement à L1.

C1 = 1/O1O2 - 1/O1D soit 1/O1D = 1/O1O2 -C1 = 1/0,03-(-20) = 53,33 ; O1D = 0,019 m.

Le diamètre DD du conjugué objet du diaphragme de L2 a pour valeur : D*O1D / O1O2 = 0,1*0,019/0,03 = 0,063 m.

Le diaphragme d'ouverture est celui de L2 : car DD<D et D entre O1 et O2.

Les conjugués du diaphragme d'ouverture dans les différents espaces (objet, image ou intermédiaire) sont appelés pupilles. Les conjugués du diaphragme de champ sont nommés lucarnes.

position de la pupille d'entrée AD= A O1 +O1D= 0,5 + 0,019 = 0,519 m.

la position de la lentille L1 est donnée par AO1 = 0,5 m ; le diamètre du diaphragme de cette lentille est D= 0,01 m.

La lucarne d'entrée est donc le diaphragme de L1.

dimension du champ total objet : 44 cm

taille minimale h'm = hm-½ dimension du champ objet = 1,6 -0,22 = 1,38 m.

une personne plus petite peut donc être visible.

quelques propriétés du laser

 On utilise couramment des lampes à vapeur de sodium ( émission spontanée lNa= 589,3 nm) et des lasers He - ne ( émission stimulée lHe - Ne = 632,8 nm).

  1. Lumière émise :
    - Citer trois caractéristiques différenciant l'émission stimulée de l'émission spontanée.
    - La puissance lumineuse émise par un laser de puissance 0,5 W est inférieure à celle d'une lampe à vapeur de Na classique. Pourquoi est-il dangereux d'observer directement un laser, alors que ce n'est pas le cas pour une lampe à vapeur de sodium ?
    - Calculer la fréquence n0 du laser He - Ne.
    - L'émission stimulée d'un photon de longueur d'onde l0= 632,8 nm est liée au passage du système du niveau d'énergie E1 au niveau de plus faible énergie E2. DE= E2-E1. Calculer DE.
    h= 6,62 10-34 Js ; 1eV= 1,6 10-19 J ; c= 3 108 m/s.
  2. Cavité résonante : de manière très simplifiée, la cavité laser est constituée de deux miroirs plans, distants de L, se faisant face.
    - Ecrire pour cete cavité la condition de résonance. Pour cela exprimer L en fonction de l.
    - On appelle n0 la fréquence d'émission du laser. L'intensité I(n) de la raie d'émission possède un profil de la forme:

    Donner deux raisons justifiant que l'on n'ait pas Dn=0.

  3. Le faisceau lumineux : le laser possède les caractèristiques suivantes : l0 = 632,8 nm ; w0=0,6 mm. On rappelle :

    - Calculer le dmi-angle d'ouverture du faisceau et la distance de Rayleigh ZR du laser .
    - Un centimètre après le waist objet, le diamètre du faisceau a toujours pour valeur 2w0. Justifier.
    - On focalise le faisceau précédent à l'aide d'une lentille de distance focale image f'=10 mm . Le waist objet est situé au foyer objet de la lentille. Où se trouve le waist image ?
    - Calculer la valeur du waist image w'0 et la divergence du faisceau après le waist image.

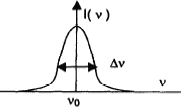
corrigé
faisceau de lumière cohérente, très directif et pratiquement monochromatique.

La puissance par unité de surface est très grande : l'énergie émise est concentrée dans une direction privilégiée.

fréquence n0 = c/l0 = 3 108 / 632,8 10-9 = 4,74 1014 Hz.

DE= h n = 6,62 10-34*4,74 1014 = 3,14 10-19 J soit 3,14 10-19 / 1,6 10-19 = 1,96 eV.

condition de résonance : L= ½k l avec k nombre entier.

largeur naturelle des raies et effet Doppler du à l'agitation thermique

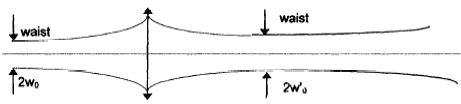
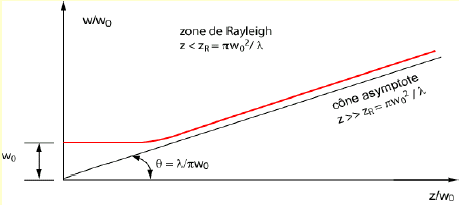
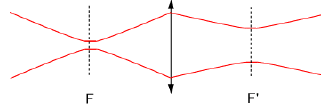
La « taille » du faisceau est appelé waist. w0 est le plus petit waist du faisceau

q= l/(pw0) = 632,8 10-9 / (3,14*0,6 10-3 )= 3,36 10-4 rad.

ZR= p w0²/l0 = 3,14 *(0,6 10-3)2/632,8 10-9 =1,78 m.

une longueur d'un cm est très faible devant ZR.

Transformation par une lentille

la formule classique de conjugaison est remplacée par : 1/s’ - 1/(s+zR2/(s+f)) = 1/f’

avec les notations suivantes (les distances sont algébriques)

s: distance lentille-waist objet

zR : distance de Rayleigh objet

s ’ distance lentille-waist image

dans ce cas s =0 le waist objet est au foyer objet de la lentille.

d'où :1/s’ - 1/(zR2/f) = 1/f’ ; 1/s’ = f/zR2 + 1/f' = -0,01 / 1,78² + 1/0,01 = -3,15 10-3+100 voisin de 100

s’ = 0,01 m ;

si on place le waist d’un faisceau laser au foyer objet d’une lentille, on trouve un waist au foyer imagede cette lentille.

w'0 = w0 f '/ZR car s =0 ; w'0 = 6 10-4 *0,01 / 1,78 = 3,37 10-6 m.

divergence du faiseceau après le waist image q'= l/(pw'0) = 632,8 10-9 / (3,14*3,37 10-6 )=0,06 rad.



retour -menu