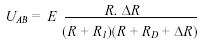|
d'après BTS chimiste 03 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
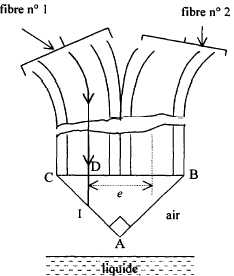
Un explosimètre a pour but d’estimer le danger d’explosivité d’une atmosphère polluée en gaz inflammable. On provoque dans une enceinte calorifugée contenant un volume donné d’un échantillon de l’atmosphère à analyser l’oxydation catalytique du gaz. L’élévation de température Dq qui en résulte est mesurée à partir de la variation de résistance électrique de l’élément détecteur RD placé dans un pont de Wheatstone (circuitCADB) selon la figure 1 ci-dessous : 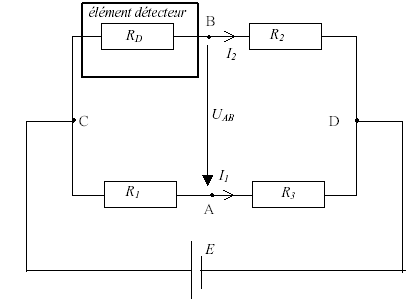
On procède à l’équilibrage du pont en présence d’air pur à 20,0 °C.
corrigé uAB= uAC+uCB=0 soit -uAC= uCBsoit uCA= uCB R1I1=RDI2 soit : I1/I2= RD/ R1 uAB= uAD+uDB=0 soit uAD= -uDBsoit uAD= uBD R3I1=R2I2 soit : I1/I2= R2/ R3 d'où : RD/ R1= R2/ R3 ; RDR3= R1 R2. si R2=R3=R
alors RD=R1.
uCD= E= (R1+R)I1 soit I1 = E / (R1+R) uCD=E= uCA+uAB+uBD= R1I1+uAB+ R2I2= R1I1+uAB+ RI2 soit uAB= E -R1I1-RI2 remplacer I1 et I2 par leurs expressions, mettre E en facteur commun : uAB= E- R1 E / (R1+R)-RE / (R1+DR+R) = E[ 1-R1 / (R1+R)- R / (R1+DR+R)] réduire au même dénominateur (R1+R)(R1+DR+R) uAB=E[ (R1+R)(R1+DR+R) -R1 (R1+DR+R) - R (R1+R) ] / [(R1+R)(R1+DR+R)] effectuer au numérateur : R1² +R1DR +R1R+RR1+RDR+R² - R1²-R1DR-R1R- R R1-R²= RDR uAB=E RDR / [(R1+R)(R1+DR+R)]. si DR négligeable devant R et R1 alors uAB=E RDR / [(R1+R)2]. uAB=E
R / [(R1+R)2] DR ; uAB et DR
sont proportionnelles
.
pour une températute q 1=q+Dq, la résisatnce RD prend la valeur : RD +DR RD +DR = R0(1 + a(q+Dq) )= R0 + R0aq +R0aDq soit DR =R0aDq autre méthode , dériver RD = R0(1 + aq ) par rapport à q : dRD = R0adq uAB=E R / [(R1+R)2] R0aDq. Application numérique : calcul de R1 = 13,4(1+1,05 10-3*20)=13,68 W. uAB= 15*100 /(13,68+100)²*13,4*1,05 10-3Dq = 1,63 10-3 Dq si Dq
= 20°C alors uAB= 1,63 10-3 *20 = 33
10-3 = 33
mV.
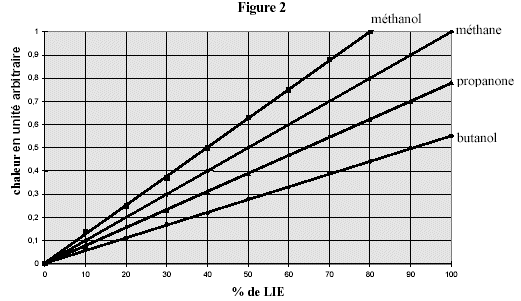
or uAB= 1,63 10-3 Dq d'où Q=C uAB/ 1,63 10-3= 1000C/1,63 uAB ; Q = constante *uAB . dans le cas du méthane Q=1 pour uAB= 0,1 V ; constante = 1/0,1 = 10. dans le cas de la propanone : Q=0,78 (lecture graphe pour LIE=100 %) soit une tension uAB= 0,78 / 10 = 0,078 V = 78 mV.
|
|
|
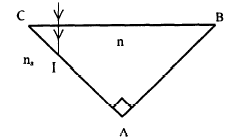
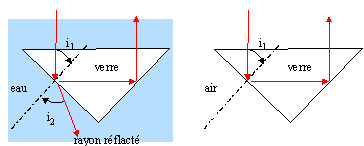
- Préciser sur un schéma le trajet du rayon lumineux après le
point I tant que le niveau du liquide n'atteint pas le point I. corrigé calcul de l'angle limite d'incidence au delà duquel il y a réflexion totale : interface verre-air : 1,52 sin i1lim= 1 soit sin i1lim=1/1,52 = 0,658 ; i1lim=41,1° or l'angle d'incidence i1=45 °, valeur supérieure à 41,1 °donc il y a réflexion totale en I. interface verre-eau : 1,52 sin i1lim= 1,33 soit sin i1lim=1,33/1,52 = 0,875 ; i1lim=61,1° or l'angle d'incidence i1=45 °,valeur inférieure à 61°, donc le rayon réfracté ( transmis dans l'eau) existe en I calcul de i2 : 1,52 sin 45 = 1,33 sin i2 ; sin i2 =0,808 ; i2 =53,9°
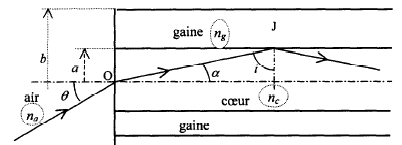
calcul de l'angle limite d'incidence au delà duquel il y a réflexion totale en J interface coeur-gaine: nc sin ilim= ng soit sin ilim= ng/nc = 0,99 ; ilim=81,89° si i<ilim il y a réflexion totale en J. en O, interface air-coeur : sin q1 = nc sin alim avec alim + ilim= 90° donc sin alim = cos ilim cos2 ilim = 1-sin2 ilim= 1-(ng/nc)2. sin 2 q1 = nc2 sin2 alim d'où sin 2 q1 = nc2 [1-(ng/nc)2] ; sin 2 q1 = nc2 -ng2. sin 2 q1 = nc2 [1-0,992]=0,0199 nc2 ; prendre la racine carrée sin q1 =0,141 nc = 0,141*1,5 =
0,2116 ; q1 =12,21°.
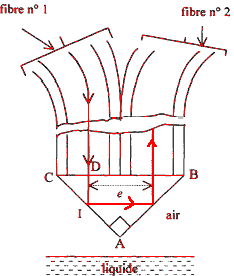
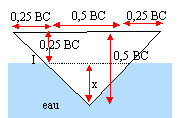
Lorsque le liquide atteint le point I, le faisceau incident se partage en deux parties : un rayon réfléchi ( figure ci-dessus) et un rayon transmis dans le liquide (eau). Le détecteur situé à l'extrémité de la fibre 2 reçoit donc beaucoup moins d'énergie lumineuse que dans le cas de la réflexion totale. profondeur à laquelle est enfoncé le prisme dans l'eau : x= 0,25 BC 0,5 BC=e=10 mm ; x= 5 mm.
Un tel dispositif permet de déclencher une alerte lorsque la montée d'un liquide atteint un niveau qui peut devenir dangereux. ou bien dans le cas de descente du liquide, indiquer le volume minimale de liquide à partir duquel il faut remplir la cuve.
|
||
|
La fibre optique étudiée ici peut être considérée comme constituée par un coeur cylindrique en matériau très transparent, le silicium, d'indice de réfraction n1 = 1,454, entouré d'une gaine concentrique au coeur, en silicium dopé, transparente elle aussi, d'indice de réfraction n2 = 1,460 . Un revêtement plastique protège l'ensemble. Un rayon R, injecté en 0 dans le coeur de la fibre, demeure prisonnier du coeur si son angle d'incidence i est bien choisi. on note r l'angle sortant du coeur de la gaine ( i,r) et on note r' l'angle incident à l'interface coeur gaine ( r + r'= 90 degrés) 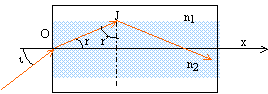
corrigé à l'interface coeur-gaine : réflexion totale en J écrire la loi de Descartes pour la réfraction : n2 sin r' limite = n1 sin 90 = n1 r' limite = sin -1 ( n1/n2) = sin -1(1,454/1,460 )= sin -1(0,9958) r' limite = 84 ,8°. r+ r'=90 donc sin r = cos r' sin² r' + cos² r' = 1 soit cos² r' = 1-sin² r'= 1-(n1²/n2²) pour l'angle limite cos r ' = racine carrée [1-(n1²/n2²)] = racine carrée [(n2²-n1²)/n2²)] = 1/n2 racine carrée (n2²-n1²) en O loi de Descartes pour la réfraction : na sin i = n2 sin r = n2 cos r' na sin i <= n2 *1/n2 racine carrée (n2²-n1²) = racine carrée (n2²-n1²) application
numérique : sin i m = (1,46²-1,454²)½ =0,132 ; im
= sin-1 (0,132 ) = 7,6
°.
par intégration [1/P]PoP =a [x]0x ; ln P-ln P0 = a x ; ln (P/P0 )= a x ln : logaritme népérien = 2,3 * log décimal 2,3 log( P/P0 )= a x ; 2,3*10 log( P/P0 )= 10 a x ; 10 log( P/P0 )= 10/2,3 a x = A x atténuation au bout de 100 km : 0,4*100 = 40 dB 10 log ( P/P0 ) = - 40 ; signe moins car diminution de 40 dB log( P/P0 ) = -4 ; P/P0 = 10-4 ; P= P0 10-4 = 10-6*10-4 = 10-10 W. |
||
|
|