pile - le radium -

titrage acido-basique- solubilité

d'après bac STL biochimie génie biologique 2002

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


pile

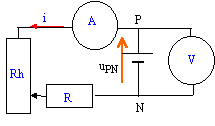
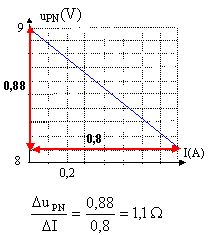
On associe en série une pile, un rhéostat, une résistance de protection, un ampéremètre et un voltmètre permettant de mesurer la tension uPN aux bornes de la pile.
uPN volt
9
8,89
8,78
8,66
8,56
8,35
8,12
I(A)
0
0,1
0,2
0,3
0,4
0,6
0,8

  1. Faire le schéma du montage.
  2. Tracer uPN=f(I)
  3. Déduire du graphe la force électromotrice E et la résistance interne de la pile
  4. On relie un générateur linéaire de fem E=9 V et de résistance interne r=1,2 ohms à une portion de circuit comprenant un moteur ( fcem E'=4 V, r'= 2 ohms) et un conducteur ohmique R=20 ohms associés en série.
    - Déterminer l'intensité du courant dans le circuit.
    - Calculer la puissance reçue par le moteur, la puissance dissipée par effet joule dans le moteur, la puissance dissipée par effet joule dans le circuit.

     

corrigé
La fem de la pile vaut E=9 V, ordonnée à l'origine.

uPN = E-rI

tension aux bornes du moteur :uMoteur = E'+r'I

tension aux bornes du résistor : urésistor = RI

moteur et résistor en série : uMoteur + urésistor =uPN

E-rI = E'+r'I +RI d'où I= (E-E') / (r+r'+R) = (9-4) / (1,2+2+20) = 0,213 A.

puissance reçue par le moteur : (E'+r'I) I= (4+2*0,213)*0,213= 0,943 W.

puissance joule dans le moteur : r'I²= 2*0,213²=  0,091 W.

puissance joule dans le circuit : (r+r'+R)I²= (1,2+2+20)*0,213²=1,05 W.


radium

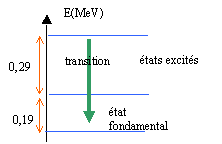
Un atome de radium 22688Ra est radioactif; il conduit au radon Rn et à noyau d'hélium 42He

  1. De quel type de radioactivité s'agit-il ?
    - Ecrire l'équation de la désintégration en citant les lois utilisées.
  2. Le diagramme énergétique de l'atome de radon est le suivant :
    - Calculer la longueur d'onde l du rayonnement émis lors de la transition représentée ci-dessus. Donner sa valeur en mm. dans quel domaine de rayonnement se situe-t-elle ?
  3. La période radioactive T ou demi-vie du radium est 1620 ans. Un échantillon de radium a une masse de 1 mg
    - Quelle masse de radium restera-t-il au bout de 3240 ans ?

    Données : mRa= 225,9972 u ; mRn= 221,9703 u ; mHe=4,0015 u

    1 u = 6,67 10-27 kg ; 1MeV= 1,6 10-13 J ; h= 6,62 10-34 Js ; c= 3 108 m/s.

     

corrigé
radioactivité de type a

22688Ra = AZX + 42He

conservation de la charge : 88=Z+2 d'où Z=86 , élément radon Rn

conservation du nombre de masse : 226=A+4 d'où A=222.

différence d'énergie associée à la transition : DE=0,48 eV= 0,48*1,6 10-19 J= 0,768 10-19 J

fréquence de la radiation émise : n =DE / h = 0,768 10-19 / 6,62 10-34 = 1,16 1014 Hz

longueur d'onde dans le vide l= c/n =3 108 / 1,16 1014 = 2,58 10-6 m = 2,58 10-3 mm

la radiation appartient au domaine UV

3240 ans = 2 périodes

au bout d'une période le nombre d'atomes radioactifs est divisé par 2

au bout de 2 périodes le nombre d'atomes radioactifs est divisé par 4

masse de radium au bour de 2 périodes : 1/4 = 0,25 mg.

titrage acido-basique

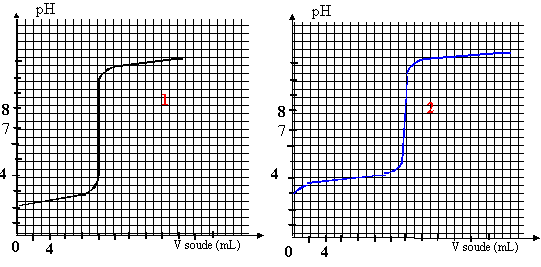
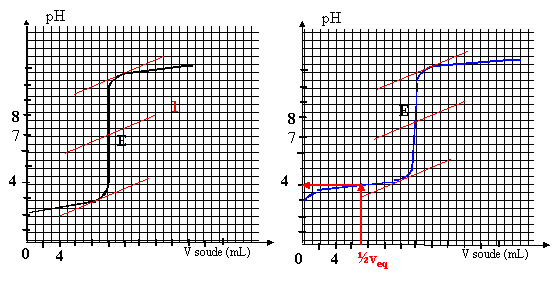
 On titre un volume V1= 20 mL d'une solution d'acide HA1 ( courbe 1) de concentration C1 puis un volume V2= 20 mL d'une solution d'acide HA2 ( courbe 2)de concetration C2 avec de l'hydroxyde de sodium (soude) de concentration c0=0,01 mol/L. On suit au pHmètre les variations de pH.

  1. D'après l'allure des courbes , préciser la nature forte ou faible des acides HA1 et HA2.
  2. Ecrire les équations des réactions de ces deux acides avec l'eau.
  3. Donner l'expression de la constante d'acidité de l'acide faible.
  4. Déterminer les coordonnées du point équivalent en précisant la méthode. Ces résultats sont-ils en accord avec la question 1
    - Ecrire les équations bilans des réactions de dosages et en déduire les concentrations c1 et c2.
    - Déduire de la courbe le pka de l'acide faible.
  5. On désire fabriquer une solution tampon à pH=pKa .
    - Qu'est-ce qu'une solution tampon ?
    - Lequel des acides doit-on choisir ? Justifier.
    - Comment faut'il procéder ? Indiquer les volumes des solutions à utiliser.
corrigé
 HA1 est un acide fort, le pH à l'équivalence est égal à 7.

HA2 est un acide faible, le pH à l'équivalence est différent de 7.

 

HA1 + H2O--> A1- + H3O+ réaction totale

HA2 + H2O= A2- + H3O+ réaction très limitée

constante d'acidité Ka= [A2-][H3O+]/[HA2]

HA1 +HO--->A1- +H2O

à l'équivalence la quantité de matière d'acide est égale à la quantité de matière de soude ajoutée

C1 V1 = c0V1équi avec V1équi = 10 mL

C1 = 0,01*10/20 = 0,005 mol/L.

HA2 +HO--->A2- +H2O

à l'équivalence la quantité de matière d'acide est égale à la quantité de matière de soude ajoutée

C2 V2 = c0V2équi avec V2équi = 14 mL

C2 = 0,01*14/20 = 0,007 mol/L.

on trouve graphiquement le pKa de l'acide faible en déterminant le pH à la demi-équivalence ( courbe 2): pKa = 4.

Une solution tampon modère les variations de pH dus à l'ajout modéré d'acide ou de base forte.

le pH d'une solution tampon ne varie pas par dilution

Une solution tampon doit contenir un couple acide base telle que l'acide et la base conjuguée soit en quantité égale.

prendre l'acide HA2 et arrèter le dosage à la demi-équivalence.

pile et solubilité

La première demi-pile est constituée d'une électrode de platine plongeant dans une solution de permanganate de potassium K+ + MnO4- acidifiée dans laquelle [MnO4-]=0,01 mol/L ; [Mn2+]=0,02 mol/L ; [H3O+]=0,01 mol/L.

L'autre demi-pile est une électrode d'argent plongeant dans une solution de nitrate d'argent Ag++ NO3- telle que [Ag+]=0,1 mol/L. L'étude est faite à 25°C.

  1. Exprimer puis calculer les valeurs des potentiels E1 et E2 de chaque demi-pile.
    - Préciser la polarité des électrodes.
    - Calculer la valeur de la fem E de la pile au début de fonctionnement.
    - Ecrire l'équation bilan de la réaction chimique lorsque la pile débite. Préciser les espèces réduites et oxydées.
  2. Déterminer la solubilité du sulfate d'argent dans l'eau pure à partir de la valeur de Ks.
    - On remplace la demi-pile n°2 par une demi-pile n°3 constituée par une électrode d'argent plongeant dans une solution de sulfate d'argent saturée. Calculer la valeur du potentiel E3 de la demi-pile n°3.
    - Au début du fonctionnement de cette pile comment évolue qualitativement la concentration en ion Ag+ dans le compartiment de la demi-pile ?

potentiel standart des couple MnO4-/Mn2+ : 1,51 V ; Ag+/Ag : 0,8 V ;

produit de solubilité Ag2SO4 : Ks= 2,4 10-5.

corrigé
MnO4-+ 8H++5e-=Mn2++4H2O

E1= E10 + 0,06 / 5 log [MnO4-][H+]8/[Mn2+]

E1= 1,51+0,06/5 log(0,01*10-16/0,02)=1,51-0,195 = 1,314 V

Ag++e- = Ag(s)

E2= E20 + 0,06 log [Ag+] = 0,8+0,06log0,1=0,74 V

fem de la pile : E=1,314-0,74 = 0,574 V.

MnO4-+ 8H++5e-=Mn2++4H2O réduction de l'oxydant le plus fort (borne positive de la pile)

5 Ag(s) = 5Ag++5e- oxydation de l'argent , réducteur le plus fort( borne négative de la pile)

bilan : MnO4-+ 8H++ 5 Ag(s) = Mn2++5Ag++4H2O

Ag2SO4 (s)= 2Ag+ + SO42- avec s=[Ag+]=2[SO42-]

Ks = [Ag+]2[SO42-] =s2 ½s= ½s3 = 2,4 10-5.

d'où la solubilité s= racine cubique(4,8 10-5)=0,0364 mol/L.

demi pile n°3 :

2Ag++2e- = 2Ag(s) et Ag2SO4 (s)= 2Ag+ + SO42-

Ag2SO4 (s) +2e- = 2Ag(s) + SO42- ; E3= E30 + 0,03 log 1/[SO42-]

E3= E20 + 0,03 log [Ag+]2 =E20 + 0,03 log [Ag+]2 [SO42-] / [SO42-]

E3= E20 + 0,03 log Ks / [SO42-]= E20 + 0,03 log Ks + 0,03 log1/[SO42-]

E3= 0,8 +0,03 log( 2,4 10-5)+ 0,03 log1/[SO42-]

E3= 0,661 + 0,03 log(1/[0,5*0,0364])= 0,661+0,03*1,74 = 0,713 V.

tant que la solution reste saturée en sulfate d'argent la concentration en ion Ag+ reste constante.


retour -menu