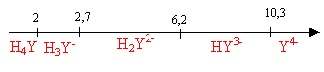Aurélie jan 04

 

cinétique d'une réaction de complexation

d'après bac STL CLPI j2003

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


cinétique d'une réaction de complexation Antilles 03

 On se propose d'étudier la réaction de complexation des ions chrome (III) par l'EDTA, en solution aqueuse maintenue à pH = 5,1.Constante de dissociation de l’ion complexe [CrY]- : KD = 1,0 . 10-23
Constante de formation de l’ion complexe [CrY]- : β = 1,0 . 1023
a) Donnez l’expression de la constante de dissociation ou de la constante de formation
du complexe [CrY]-.

Données (à 25 °C) :

L'EDTA est introduit sous forme de sel disodique Na2H2Y qui se dissocie totalement en ions Na+ et H2Y2- en solution.

· pKa de l'EDTA, H4Y, en solution aqueuse :

pKa1 (H4Y/H3Y-) = 2,0 ; pKa2 (H3Y-/H2Y2-) = 2,7 ; pKa3 (H2Y2-/HY3-) = 6,2 ; pKa4 (HY3-/Y4-) = 10,3

· Constante de dissociation de l'ion complexe [CrY]- : KD = 1,0 10-23.

  1. Etude des équilibres acido-basiques.
    - Sur une échelle de pH, indiquer les domaines de prédominance des espèces acido-basiques de l'EDTA en fonction du pH. Préciser l'espèce prédominante à pH = 5,1.
    - Donner les expressions des constantes Ka3 et Ka4.
    - Exprimer la concentration [Y4-] en solution en fonction des constantes d'acidité Ka3, Ka4, de la concentration en H3O+ et de la concentration [H2Y2-].
    - En admettant que la concentration [H2Y2-] est constante, égale à 0,100 mol.L-1, calculer la valeur numérique de la concentration [Y4-] en solution à pH = 5,1.
  2. Etude de la réaction de complexation : dans la solution contenant l'ion H2Y2- à la concentration de 0,100 mol.L-1, maintenue à pH = 5,1, on introduit des ions Cr3+ à raison de 3,0 10-3 mol.L-1. On admettra que la concentration [Y4-] reste constante, égale à 5,0 10-8 mol.L-1, tout au long de la réaction de complexation.
    - Donner l'expression de la constante de dissociation du complexe [CrY]-.
    - Montrer que la réaction de complexation est pratiquement totale, en calculant la concentration des ions Cr3+ à l'équilibre.
  3. Etude cinétique de la réaction de complexation : dans cette question, l'équation de la réaction est écrite sous la forme : Cr3+ + H2Y2- = [CrY]- + 2 H+ . La réaction est totale ; elle est d'ordre partiel 1 par rapport aux ions Cr3+ et d'ordre partiel 1 par rapport à H2Y2- La constante de vitesse est notée k.
    La solution contient initialement C0 = [Cr3+]0 = 3,10-3 mol.L-1 d'ions Cr3+ et [H2Y2- ]0 = 0,100 mol.L-1 d' ions H2Y2-. On suit le déroulement de la réaction, à température, volume et pH constants, de façon à déterminer la concentration en ions Cr3+ non complexés (notée C) en fonction du temps écoulé t :
    t (min)
    0
    10
    20
    30
    40
    60
    90
    120
    C (mol.L-1)
    3 10-3
    2,7610-3
    2,55 10-3
    2,35 10-3
    2,16 10-3
    1,83 10-3
    1,43 10-3
    1,12 10-3

    - Donner l'expression de la vitesse de la réaction en fonction de k, constante de vitesse, et des concentrations [H2Y2-] et [Cr3+].
    - Montrer que la concentration [H2Y2-] peut être considérée comme constante. Donner alors une expression simplifiée de la vitesse de réaction, en introduisant une constante k' égale à k[H2Y2-]0.
    - Vérifier que la loi cinétique est alors du type: log(C0/C) = k't par une méthode graphique.
    - Donner la valeur de k'. Préciser son unité. 

corrigé

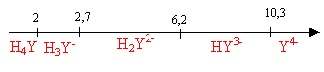
à pH=5,1 , H2Y2- prédomine.

Ka3 associé à l'équilibre acide base H2Y2-+ H2O=HY3-+ H3O+ : Ka3 = [HY3-][H3O+] / [H2Y2-] (1)

Ka4 associé à l'équilibre acide base HY3- + H2O=Y4-+ H3O+ : Ka4 = [Y4-][H3O+] / [HY3-] (2)

(1) donne : [HY3-] =Ka3[H2Y2-] / [H3O+]

(2) donne : [Y4-] =Ka4[HY3-]/ [H3O+] = Ka4Ka3[H2Y2-] /([H3O+])²

[H2Y2-] = 0,1 ; [H3O+] = 10-5,1 = 7,94 10-6 mol/L ; Ka4= 10-10,3 =5 10-11 ; Ka3= 10-6,2 =6,3 10-7 ;

[Y4-] = 6,3 10-7 *5 10-11 *0,1 / (7,94 10-6)²= 5 10-8 mol/L.

[CrY]- = Y4- + Cr3+ constante associée KD =[Cr3+][Y4-] / [[CrY]-] = 10-23

[Y4-] =5,0 10-8 mol/L ; [Cr3+]*5,0 10-8 / [[CrY]-] = 10-23 ; [Cr3+] / [[CrY]-] =10-23 / (5 10-8 )= 2 10-16.

[[CrY]-] =[Cr3+] /2 10-16 = 5 1015 [Cr3+]

conservation de l'élément chrome : [Cr3+] + [[CrY]-] = 3 10-3 =[Cr3+] + 5 1015 [Cr3+] = 3 10-3;

[Cr3+] = 6 10-19 mol/L

donc la réaction de complexation est totale ( pratiquement tous les ions chrome (III) ont disparu de la solution)

vitesse de formation du complexe v= k [H2Y2-] [Cr3+].

H2Y2-est en large excès devant Cr3+ ; [H2Y2-] peut être considérée comme une constante égale à [H2Y2-]0

par suite v = k [H2Y2-]0 [Cr3+] = k'[Cr3+]

t (min)
0
10
20
30
40
60
90
120
C (mol.L-1)
C0 =3 10-3
2,7610-3
2,55 10-3
2,35 10-3
2,16 10-3
1,83 10-3
1,43 10-3
1,12 10-3
C0/C
1
1,086
1,176
1,277
1,39
1,64
2,10
2,68
log(C0/C)
0
0,036
0,07
0,106
0,142
0,215
0,32
0,43
log(C0/C)/t
xxxxxx
3,6 10-3
3,5 10-3
3,53 10-3
3,55 10-3
3,58 10-3
3,55 10-3
3,56 10-3
k'= 3,55 10-3 min-1.

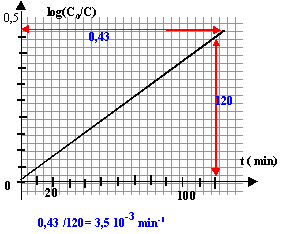
la courbe est une droite, donc la loi log(C0/C) = k't est bien vérifiée

retour -menu