|
d'après bac Polynésie 2004 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||
|
|||
|
|
Une corde métallique verticale de longueur L= 1 m est attachée à son extrémité supérieure à un support fixe. Son extrémité inférieure est quasiment immobilisée par une plaque percée d'un petit trou dans lequel passe la corde. La corde est tendue par une masse M accrochée à son extrémité inférieure. Elle est parcourue par un courant électrique sinusoïdal de fréquence 50 Hz. On dispose un aimant en U à cheval sur le fil, au voisinage du milieu de la corde. Pour certaines valeurs de M la corde prend un aspect particulier : on y observe un système d'un ou plusieurs fuseaux stables de même longueur. g= 10 m/s². La célérité d'une onde se propageant sur une corde tendue est v= (T/m)½ où T est la tension de la corde en newton et m la masse linéïque ( masse par unité de longueur en kg /m). 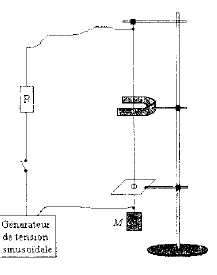
Un seul fuseau : donc la corde vibre suivant son mode fondamental et L=½l soit l = 2 m. v = l f = 2*50 = 100 m/s. La masse accrochée à l'extrémité inférieure est immobile sous l'action de son poids et de la tension du fil : le principe d'inertie conduit à : T=Mg . expression de la masse linéïque : m=m / L avec m : masse (kg) de la corde. v = (T/m)½ soit v²= T/m = Mg L/ m d'où m = MgL/v² m= 2*10*1/100² =
0,002 kg = 2g.
la fréquence étant inchangée, la célérité doit donc diminuée or v = (T/m)½ = (MgL/m)½ avec g, L et m des constantes donc si la masse M diminue on peut obtenir plusieurs fuseaux. Pour trois
fuseaux le point du milieu de la corde vibre avec une amplitude maximum
et constitue un ventre de vibration.
nouvelle célérité v ' =( MgL/(4m))½ = ½( MgL/m)½ =½v = 50 m/s. nouvelle longueur d'onde : l' = v'/f = ½l = 1 m. On observe 2 fuseaux : l'aimant placé au centre se trouve en face d'un noeud de vibration ; il faut le déplacer afin de l'amener au quart de la corde ( il sera alors en face d'un ventre de vibration)
|
||
|
|
|||
|
|