|
l'aspirine - solubilité et complexe En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
|
Le radium 226 88Ra se désintègre en émettant une particule a. Le noyau fils est un isotope du radon (Rn). Le radon est un gaz dans les conditions ordinaires de température et de pression. Le radium 228 88Ra est radioactif b-.
c=3 108 m/s ; 1 eV= 1,6 10-19 J ; Numéros atomiques de quelques éléments chimiques : radon Z=86 ; francium Z=87 ; radium Z=88 ; actinium Ac Z=89 ; Thotium Th Z= 90 ; proactinium Pa Z=91 masse en kg des noyaux : 42He : 6,644 65 10-27 ; 226Ra : 3,752 438 10-25 ; 222Rn : 3,685 904 10-25 . corrigé composition du noyau du nucléide 20884Po 84 protons ; 208-84 = 124 neutrons 22688Ra--> 22286Rn+ 42He. composition du noyau fils du nucléide 22286Rn 86 protons ; 222-86 = 136 neutrons Le radium 22688Ra et le radon 22686Rn ne sont pas isotopes: ils différent par leurs numéro atomique ( deux isotopes ne différent que par leur nombre de neutrons, donc possède le même numéro atomique) Le radium 228Ra est radioactif b- : 22888Ra --> AZX + 0-1e conservation du nombre de masse : 228 = A + 0 d'où A=228 conservations du nombre de charge : 88 = Z-1 d'où Z=89 Son noyau fils est un isotope de l'actinium Ac La demi-vie du radon 22286Rn est 3,8 jours. Après 1 durée t½=3,8 jours il reste N(t½) = ½N0 =50% N0. Après 2 durées t½=2*3,8 jours il reste N(2t½) = 25% N0. Après 3 durées t½=3*3,8 jours=11,4 jours il reste N(3t½) = 12,5% N0. énergie libérée par la réaction de désintégration 22688Ra--> 22286Rn+ 42He. variation de la masse |Dm |=| masse 42He + masse 2286Rn - masse 22688Ra| |Dm |=|6,644 65 10-27 + 3,685 904 10-25 -3,752 438 10-25 |=8,75 10-30 kg énergie correspondante |Dm | c²= 8,75 10-30 * (3 108)²= 7,87 10-13 joule 7,87 10-13 /1,6 10-19 = 4,92 106 eV =4,92 MeV.
|
|||||||||||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||||||||||
|
On dispose d'une ampoule de lampe de poche, d'un générateur de tension continue de fem E=4,5 V et de résistance interne r=1,5 W, d'un rhéostat dont la valeur de la résistance peut varier de 0 à 120 W, de deux multimètres, d'un interupteur, de fils de connexion. On réalise le montage ci dessous dans lequel la tension aux bornes de l'ampèremètre est négligeable. 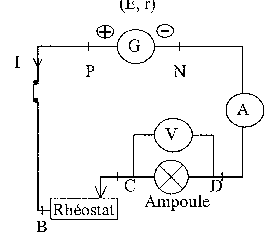
corrigé on fait varier l'intensité I du courant dans le circuit en modifiant la valeur de la résistance du rhéostat UPN=E-rI =4,5-1,5*0,2= 4,2 V. UPN=UBD= UBC+UCD soit UBC= UPN-UCD =4,2-2=2,2 V UBC= R I soit R= 2,2 / 0,2 = 11 W. puissance fournie par le générateur au circuit extérieur P1= UPN I= 4,2*0,2 =0,84 W puissance P2 dissipée par effet joule dans le générateur P2= r I²= 1,5*0,2²=0,06 W.
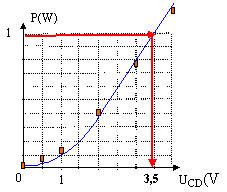
la tension aux bornes de l'ampoule est voisine de 3,5 V . D'après le tableau , l'intensité du courant est voisne de 0,28 A L'indication portée par l'ampoule : 1 W ; 0,3 A est cohérente avec ces résultats.
|
||||||||||||||||||||||||||||||||||||
corrigé 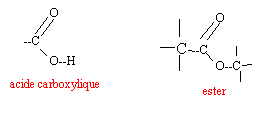
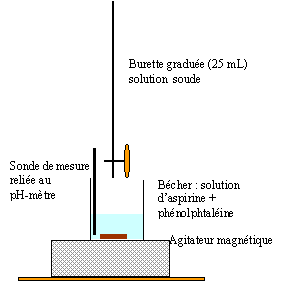
HA + H2O = H3O+ + A-. Ka = [H3O+]éq[A-]éq / [HA]éq pH= pKa + log ([A-]éq / [HA]éq) pH- pKa =1,5 -3,5 = -2= log ([A-]éq / [HA]éq) [A-]éq / [HA]éq = 0,01 soit [HA]éq = 100 fois [A-]éq., la forme acide prédomine à pH inférieur à pKa. en élevant le pH,
la diférence pH-pKa augmente et en conséquence log ([A-]éq
/ [HA]éq) augmente.
HA + HO- --> H2O + A-.
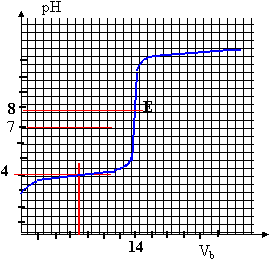
coordonnées du point équivalent E( pH = 8 et Vb= 14 mL) à l'équivalence les quantités de matière d'acide HA et de soude ajoutée sont en proportions stoéchiométriques CaVa = CbVb soit Ca = CbVb / Va =0,02*14 / 50 = 0,0056 mol/L. Qté de matière d'aspirine dans 500 mL ou 0,5 L : 0,5 * 0,0056 = 0,0028 mol masse molaire aspirine C9H8O4 : 9*12+8+4*16 = 180 g/mol quantité de matière d'aspirine dans un comprimé : 180 * 0,0028 = 0,504 g = 504 mg. dans un comprimé il y a 504 mg d'aspirine, en accord avec l'indication portée sur l'étiquette.
|
||||||||||||||||||||||||||||||||||||
masse atomique molaire (g/mol) Cl : 35,5 ; Ag : 108. produit de solubilité du chlorure d'argent : pKs = 9,8 constante de formation du complexe Kf= 1,67 107. corrigé Ag+ + Cl- = AgCl(s) Qté de matière (mol) : volume solution (L) * concentration (mol/L) ion Ag+ : 0,01*0,15 =1,5 10-3 mol en conséquence 1,5 10-3 mol de chlorure d'argent solide masse molaire AgCl : 108+35,5 =143,5 g/mol masse de précipité : 143,5*1,5 10-3 = 0,215 g. solubilité d'un composé : quantité de matière (mol ou g) que l'on peut dissoudre dans un litre de solvant. La solubilité s'exprime en mol/L ou en g/L. Ag+ + Cl- = AgCl(s) avec Ks = [Ag+ ][Cl-]= s*s= s² =10-9,8 =1,58 10-10 d'où s= 1,26 10-5 mol/L ou 1,26 10-5 * 143,5 =1,8 10-3 g/L ligand : entité chimique liée au cation central d'un complexe ; dans ce cas le ligand est l'ammoniac NH3. Ag+ +2NH3 = [Ag(NH3)2]+ Kf=[[Ag(NH3)2]+] / ([Ag+][NH3]2)= 1,67 107. conservation de l'ion argent :[Ag+] +[[Ag(NH3)2]+] = 0,15*10 / (10+10) =0,075 mol/L l'ammoniac est en large excès (1*10 / (10+10)) =0,5 mol/L) et[NH3] peut être considérée comme constante. [[Ag(NH3)2]+] / ([Ag+]*0,52)= 1,67 107. [[Ag(NH3)2]+] / [Ag+] =0,52* 1,67 107= 4,17 106. en conséquence [[Ag(NH3)2]+] très supérieure à [Ag+] ; [[Ag(NH3)2]+] voisin de 0,075 mol/L [Ag+] =0,075 / 4,17 106= 1,8 10-8 mol/L |
||||||||||||||||||||||||||||||||||||
|
|