Aurélie septembre 04

Energie d'un système ressort solide ; étude expérimentale d'une bobine ;

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


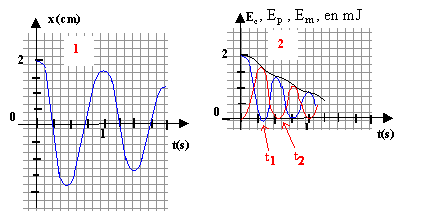
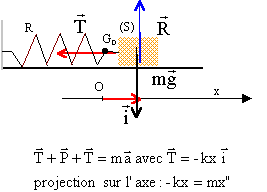
Energie d'un système ressort solide

 Le système solide ressort est constitué d'un solide de masse m = 250 g , accroché à l'extrémité d'un ressort à spires non jointives, de masse négligeable, de constante de raideur k=10 N/m.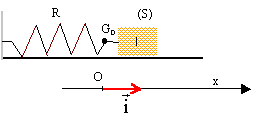

Le mobile assimilé à son centre d'inertie G peut osciller horizontalement sur une tige. On étudie son mouvement dans un référentiel galléen. Le point O correspond avec le point G lorsque le solide est au repos.

  1. Dans un premier temps on néglige les frottements du mobile sur son rail de guidage.
    - Représenter les diffrérents vecteurs forces s'exerçant sur le solide sans souci d'échelle.
    - En appliquant la seconde loi de Newton au mobile, établir l'équation différentielle du mouvement.
    - Vérifier que x = Xm cos (wt+F) est solution de cette équation différentielle quelles que soient les valeurs des constantes Xm et F.
    - Le mobile est écarté de sa position d'équilibre et lâché à l'instant t=0 s, sans vitesse initiale, de la position x0= + 2 cm, et xM >0. Déterminer Xm et F.
    - Calculer la période des oscillations propres T0 = 2p(m/k)½.
  2. On suppose maintenant que les frottements ne sont plus négligeables et peuvent être modélisés par une force f = m v dont la valeur est proportionnelle à celle de la vitesse et dont le sens est opposé à celui du mouvement. (m est positif).
    - A l'aide de la figure 1 déterminer la pseudo-période T du mouvement et la comparer à T0.
    - Identifier les courbes de la figure 2

    - Pourquoi l'énergie mécanique diminue-t-elle au cours du temps ?
    - On a repéré deux instants particuliers notés t1 et t2.Que vaut la vitesse du mobile à chacune de ces deux dates ? Justifier.
    - Conclure quant à la valeur de la force de frottement à chacun de ces instants ?
    - Justifier alors la forme "en escalier " de la courbe Em(t).

corrigé
Le solide est soumis à son poids P, à la réaction de l'axe R et à la tension T du ressort. La seconde loi de Newton s'écrit :

soit x" + k/m x = 0 ( équation différentielle du mouvement). On pose w2=k/m

x = Xm cos (wt+F) dériver deux fois pout obtenir x" :

x'= -Xm w sin (wt+F) ; x" = -Xm w2 cos (wt+F) = - w2 x

repport dans l'équation différentielle x" + k/m x = 0

- w2 x + k/m x = - w2 x + w2 x est bien nulle quel que soit x ; donc la fonction proposée est solution de l'équation différentielle.

x = Xm cos (wt+F)

à la date t=0 : x = Xm = 0,02 m soit 0,02 = 0,02 cos F ; cos F=1 ; F = 0 . x = 0,02 cos (wt) en mètre.

période des oscillations propres T0 = 2p(m/k)½ avec m = 0,25 kg et k = 10 N/m

T0 = 6,28 ( 0,25/10)½ =6,28*0,158 = 0,99 s.

pseudo-période T = 1s, propche de T0, l'amortissement restant assez faible.

A l'instant t=0, l'énergie mécanique est entierement sous forme potentielle élastique : Ep correspond à la courbe bleue.

A l'instant t=0, l'énergie cinétique est nulle : Ec correspond à la courbe rouge.

Em=Ep+Ec , l'énergie mécanique correspond à la courbe noire.

Du fait de l'amortissement, l'énergie mécanique diminue au cours du temps.

à la date t1 l'énergie cinétique ½mv2 est maximale, égale à l'énergie mécanique : la vitesse est maximale.

la valeur de la force de frottement étant proportionnelle à la valeur de la vitesse, la force de frottement est maximale

à la date t2 l'énergie cinétique est nulle : la vitesse est nulle et en conséquence :

- la force de frottement est nulle.

- l'énergie mécanique diminue très peu au voisinage de t2.( aspect en escalier de Em)


étude expérimentale d'une bobine

 

  1. On réalise le circuit ci-dessous. le GBF délivre une tension alternative triangulaire. On enregistre les tensions uL(t) aux bornes de la bobine et l'intensité i(t) du courant qui circule dans le circuit à l'aide d'un système d'aquisition.

    - Vérifier graphiquement que la fréquence du GBF est 1 kHz..
    - Quelle est l'expression de la tension mesurée sur la voie 2. En déduire les opérations que devra effectuer le logiciel de traitement des données pour visualiser i(t) sur l'éran.
    - Exprimer la tension uL aux bornes de la bobine en fonction des caractéristiques de la bobine, de l'intensité du courant et de sa dérivée i'= di/dt.
    - La représentation graphique de la fonction i(t) montre qu'en réalité les crêtes de l'intensité sont arrondies. dans ces conditions la tangente au sommet est horizontale. En déduire une expression simplifiée de uL quand l'intensité dans le circuit est extrémale.
    - Quand l'intensité est extrémale uL vaut environ 10 mV. Montrer alors que r << R.
    - On néglige par la suite le terme faisant intervenir r dans l'expressionde uL ainsi que les arrondis des crêtes de l'intensité. En travaillant sur la durée [0,1 ; 0,6 ms] mesurer uL, calculer di/dt et en déduire la valeur de L.

  2. Constante de temps d'un circuit (R, L): la bobine est maintenant montée avec une résistance R'= 100 W aux bornes d'un générateur idéal de tension de fem E= 6,5 V. r= 12 W.

    - Etablir l'expression donnant l'intensité du courant en régime permanent en fonction des caractéristiques du circuit.
    - Vérifier que la valeur de l'intensité du courant en régime permanent lue sur le graphe est en accord avec les données de l'énoncé.
    - Rappeler l'expression de la constante de temps d'un dipôle (R L).
    - Déterminer graphiquement sa valeur. Vérifier que cette valeur est en accord avec celle de l'inductance de la bobine calculée précédemment.
    - La résistance R' étant réglable, on lui donne la valeur R'=150 W. Calculer la nouvelle intensité en régime permanent, la nouvelle constante de temps du dipôle (R L) et représenter avec soin la courbe représentant l'intensité du courant en fonction du temps sur la figure donnée. 

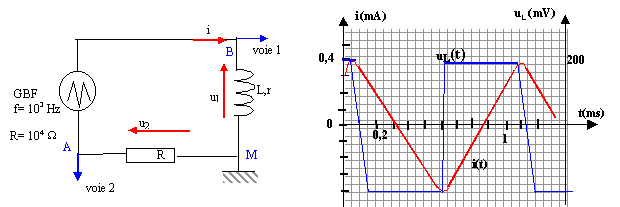
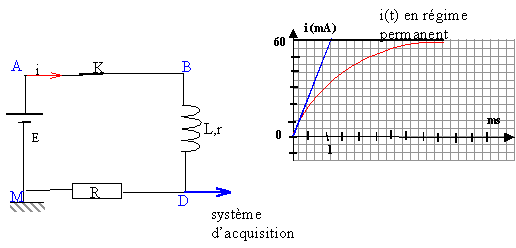
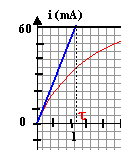
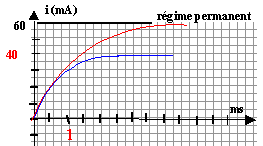
corrigé
Les fonctions i(t) et uL(t) sont périodiques, de période 1 ms = 10-3 s d'après les graphes.

La fréquence est l'inverse de la période: f = 1 / 103 = 1000 Hz = 1 kHz.

Expression de la tension mesurée sur la voie 2 : u2 = uAM = -uMA = -Ri = - 104 i

i(t) = - u2 / 104 = - 10-4 u2 (avec u2 en mV et i en mA)

le logiciel doit multiplier u2 par - 10-4 pour obtenir i(t)

tension uL aux bornes de la bobine : uL= Ldi/dt + ri.

la tangente au sommet est horizontale donc di/dt est nulle au voisinage d'une crête.

alors uL s'écrit au voisinage d'une crête : uL = riextrème.

si iextrème = 0,4 mA = 4 10-4 A ; uMA= R iextrème = 104 * 4 10-4 = 4 V

uL = riextrème= 0,01 V ; riextrème<< R iextrème soit r <<R.

sur la durée [0,1 ; 0,6 ms] : uL= - 200 mV = -0,2 V;

i(t) est fonction affine décroissante sur cet intervalle, de pente : -0,8 10-3 / 0,5 10-3 = - 1,6 A s-1.

uL= Ldi/dt donne L= uL/ (di/dt ) = -0,2/ (-1,6) = 0,125 H.

En régime permanent l'intensité étant constante, di/dt =0 et la tension aux bornes de la bobine est : uBD= r ipermanent.

de plus uDM=R'ipermanent ; uBD+ uDM= E ; (R'+r)ipermanent=E ; ipermanent = E/(R'+r).

ipermanent = 6,5 / (100+12)= 0,058 A = 58 mA en accord avec la valeur 60 mA lue sur le graphe.

constante de temps d'un dipôle (R L) : t = L / (R'+r)

L'intersection de la tangente à l'origine avec l'asymptote horizontale donne la valeur de t ; t voisin de 1,2 ms = 1,2 10-3 s.

R'= 100 W; r= 12 W et L= 0,125 H : tcalcul = 0,125 / (100+12) = 1,1 10-3 s=1,1 ms donc accord.

R'= 150 W; r= 12 W et L= 0,125 H : tcalcul = 0,125 / (150+12) = 7,7 10-4 s= 0,77 ms.

ipermanent = 6,5 / (150+12)= 0,04 A.

suivi d'une réaction lente

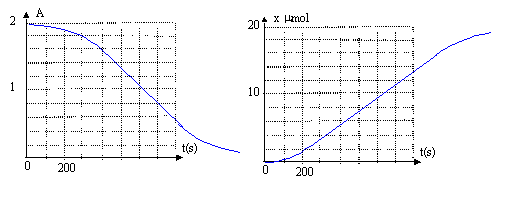
On étudie la réaction d'oxydation de l'acide oxalique HOOC-COOH ( solution incolore) par l'ion permanganate MnO4-(aq) en milieu acide ( solution de couleur violette). Le suivi de la réaction est réalisé par spectrophotométrie.

  1. On dispose d'une solution mère de permanganate de potassium de concentration c0 = 0,01 mol/L. Décrire en précisant le matériel utilisé la préparation de 50 mL de solution aqueuse de permanganate de potassium de concentration c1= 2 10-3 mol/L.
  2. La réaction met en jeu les couples : MnO4-(aq) / Mn2+(aq) ; CO2(aq) / H2C2O4(aq).
    - Ecrire les deux demi-équations d'oxydoréduction de ces deux couples pui la réaction entre les ions permanganate et l'acide oxalique.
    - On mélange V1 = 20 mL de la solution aqueuse de permanganate de potassium de concentration apportée C1, acidifiée par de l'acide sulfurique, à V2 = 20 mL d'une solution d'acide oxalique de concentration molaire apportée C2=0,05 mol/L. Quelle est à l'instant t=0 la quantité de matière n01 d'ions permanganate ? Quelle est à l'instant t=0 la quantité de matière n0 d'acide oxalique ?
    - Les ions Mn2+ ne colorent pas le milieu réactionnel. Comment va évoluer la couleur du mélange lorsque la transformation se déroule ?
  3. La transformation chimique supposée totale étant lente, on peut suivre son évolution par spectrophotométrie. On mesure l'absorbance A du mélange réactionnel placé dans la cuve du spectrophotomètre.
    - Quelle est l'espèce chimique responsable de l'absorbance de la solution ? 
    - Dans les conditions de l'expérience, la concentration des ions permanganate est proportionnelle à l'absorbance A. L'absorbance A et l'avancement de la réaction sont reliées par la relation : x(t) = (2 - A(t)) 10-5 mol.

    En quoi la courbe A=f(t) permet-elle de retrouver le réactif limitant ?

    - Définir puis déterminer en justifiant le temps de demi-réaction t½.
    - Définir la vitesse volumique de réaction en fonction de x(t)
    - Le volume restant constant, en comparant qualitativement les vitesses de réaction aux dates t1= 100 s, t2 = 600 s et t3 = 1100 s, dire comment évolue la vitesse au cours du temps.
    - On refait l'expérience en modifiant uniquement la concentration molaire apportée de la solution d'acide oxalique c'2 = 2,5 10-3 mol/L. Calculer la nouvelle quantité de matière initiale d'acide oxalmique, en déduire le réactif limitant. Quelle est l'absorbance finale ?

corrigé
facteur de dilution : c0/c1 =0,01 / 0,002 = 5.

volume fiole jaugée / volume pipette = rapport de dilution

volume pipette = 50 / 5 = 10 mL

prélever 10 mL de solution mère à l'aide d'une pipette graduée 10 mL

placer dans la fiole jaugée de 50 mL, compléter avec de l'eau distillée jusqu'au trait de jauge puis agiter pour rendre homogène.

2 fois { MnO4-+ 8H+ + 5e- = Mn2++ 4H2O }réduction

5 fois { H2C2O4 = 2CO2 + 2e- + 2H+ } oxydation .

2 MnO4- + 6 H+ + 5 H2C2O4 = 2 Mn2++10 CO2 + 8 H2O

quantité de matière n01 : C1 V1 =2 10-3 * 20 10-3 = 4 10-5 mol.

quantité de matière n0 d'acide oxalique :C2 V2 =5 10-2 * 20 10-3 = 10-3 mol.

2 MnO4-
+ 6 H+
+ 5 H2C2O4
= 2 Mn2+
+10 CO2
+ 8 H2O
initial
4 10-5 mol
excès
10-3
0
0
solvant en grande quantité
en cours
4 10-5 -2x
10-3-5x
2x
10 x
fin
4 10-5 -2xmax
10-3-5xmax
2xmax
10 xmax
si l'ion permanganate est en défaut : 4 10-5 -2xmax=0 soit xmax = 2 10-5mol

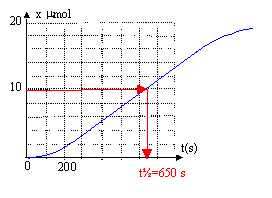
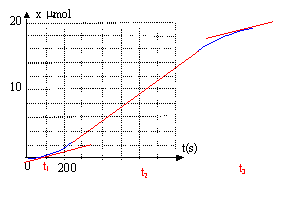
si l'acide oxalique est en défaut : 10-3-5xmax =0 soit xmax = 2 10-4 mol

l'ion permanganate est donc en défaut ( réactif limitant)

La couleur du mélange initialement violette, va s'éclaircir puis devenir incolore lorsque tout les ions permanganate seront consommés.

L'espèce chimique responsable de l'absorbance de la solution est l'ion permanganate violet ( la seule espèce colorée présente)

la courbe A=f(t) permet de retrouver le réactif limitant, l'ion permanganate, car l'absorbance finale est nulle.

Le temps de demi-réaction est la durée au bout de laquelle la moitié du réactif limitant a disparu :

l'avancement vaut alors 2 10-5 / 2 = 10-5 mol. : t½ = 650 s. (lecture graphe x(t) = f(t))

La vitesse volumique de réaction est proportionnelle à la dérivée de l'avancement par rapport au temps :

v = 1/V dx(t) / dt avec V : volume de la solution en L ; x : avancement en mol et t durée en seconde.

Graphiquement dx(t) /dt correspond au coefficient directeur de la tangente à la courbe x(t) = f(t) à la date considérée.

la vitesse est d'autant plus grande que le coefficient directeur est plus grand ou que la tangente se rapproche de la verticale.

à la date t1 et à la date t3 la vitesse est faible ( tangente presque horizontale)

à la date t2 la vitesse est grande ( tangente plus inclinée sur l'horizontale)

vitesse faible au début ( peu de catalyseur), puis la vitesse augmente ( réaction autocatalysée par l'un des produit Mn2+), puis diminue vers la fin ( la concentration des ions permanganate tend vers zéro)

quantité de matière n'0 d'acide oxalique :C'2 V2 =2,5 10-3 * 20 10-3 = 5 10-5 mol.

2 MnO4-
+ 6 H+
+ 5 H2C2O4
= 2 Mn2+
+10 CO2
+ 8 H2O
initial
4 10-5 mol
excès
5 10-5
0
0
solvant en grande quantité
en cours
4 10-5 -2x
5 10-5 -5x
2x
10 x
fin
4 10-5 -2xmax
5 10-5 -5xmax
2xmax
10 xmax
si l'ion permanganate est en défaut : 4 10-5 -2xmax=0 soit xmax = 2 10-5mol

si l'acide oxalique est en défaut : 5 10-5 -5xmax =0 soit xmax = 10-5 mol

l'acide oxalique est maintenant en défaut ( réactif limitant)

il reste : 4 10-5 -2xmax =4 10-5 -2 10-5 =2 10-5 mol d'ion permanganate.

la solution finale est encore violette et l'absorbance finale Afin est différente de zéro.

L'absorbance A et l'avancement de la réaction sont reliées par la relation : xmax = (2 - Afin ) 10-5 mol.

(2-Afin )= xmax /10-5 soit Afin = 2-xmax /10-5 = 2-10-5 /10-5 =2-1 = 1.

retour -menu