Mathématique,
Physique
chimie.
Concours technicien police technique et scientifique 2024
(sud).
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Questionnaire à choix multiple :
Pour chaque affirmation, une seule réponse est exacte. Aucune
jusüfication n'est demandée.
On considère la fonction f définie sur R par f (x)=3e-3x.
1. La dérivée de la fonction f définie sur R est égale à :
On pose u = -3x ; u' = -3 ; f ' = u' eu ; f ' = -9e-3x.
Réponse c.
2. La courbe représentative de la foncüon f admet pour asymptote :
Quand x tend vers plus l'infini, f(x) tend vers zéro ; l'axe des abscisses y= 0 est asymptote.
Réponse a.
3. Une solution de l'équaüon différentielle y' +3y=0,6 est la fonction
g définie par :
Solution générale de y'+3y=0 : y = A e-3x avec A une constante.
Solution particulière : y = 0,6 /3 = 0,2.
Solution générale de y' +3y=0,6 :
y = A e-3x +0,2 soit f(x) +0,2. Réponse d.
4. On considère une variable aléatoire X qui admet pour densité la
fonction f.
L'espérance f (X) vaut :
f est une densité d'une loi exponentielle de paramètre l = 3.
E(x) = 1 / 3. Réponse c.
5. L'intégrate suivante vaut :

Réponse a.
Exercice 1 : Prix de l'électricité en France
Le prix de l'électricité en France a subi une augmentation historique :
+15% en février 2023, + 10% en août 2023 et +5% en février 2024.
On suppose que l'augmentaüon de l'électricité se stabilisera désormais
à +5% par an.
Les résultats seront arrondis à 10-3 si nécessaire.
On note un, le prix (en euro) d'un kilowattheure au 1er février de I'année
2024+n.
1. Sachant que le prix du kilowattheure était de 0,2276 € en Janvier
2024; calculer u0, le prix en euro d'un kilowattheure au 1er février 2024.
u0 = 0,2276 x1,05 ~0,239 €.
2. On estime qu'un foyer moyen en France consomme 5 700 kWh par an,
calculer le prix de sa consommation électrique entre le 1er février 2024 et le 31
janvier 2030.
Somme des 6 premiers termes d'une suite géométrique de raison 1,05 et de premier terme 5700 x 0,23898 =1362,186 €.
1362,186 (1-1,056) / (1-1,05)=9265,47 €.
Un
fournisseur d'électricité propose un contrat avec une réducüon de 1
centime d'euro sur le prix du kilowattheure, après l'augmentaüon
annuelle de 5% au 1er 'février. On note v, le prix en euro du
kilowattheure au 1er février de l'année 2024+n.
1.3.1. Justifier que la suite (vn) vérifie :
vn+1= 1 ,05 vn-0,01.
Le prix augmente de 5 % chaque année ; et il y a une réduction de 1 centime.
vn+1= 1 ,05 vn-0,01.
La première année le prix est : v0 ~0,239
1.3.2. On considère la suite (wn) définie par wn= vn-0,2
Montrer que la suite (wn) est géométrique de raison 1,05. En déduire
l'expression de wn en fonction de n puis celle de v, en fonction de n.
wn+1= vn+1-0,2 =1 ,05 vn-0,01-0,2 = 1,05 vn-0,21 =1,05(vn-0,2) =1,05 wn.
w0 = v0 -0,2 ~0,039.
wn = w0 x1,05n= 0,039 x1,05n.
vn = wn +0,2 = 0,039 x1,05n+0,2.
1.3.3 A partir de quelle année la promotion de ce fournisseur
d'électricité permettra d'avoir le prix d'un kilowattheure deux fois moins élevé que
le tarif réglementaire ? Justifier.
un = u0 x1,05n =0,239 x1,05n.
vn = 0,039 x1,05n+0,2 = 0,5 un = 0,1195 x1,05n.
1,05n(0,1195-0,039) =0,2 ; 0,0805 x 1,05n = 0,2.
1,05n =2,484 ; n = ln(2,484) / ln(1,05) =18,65 soit 19 ans.
Exercice 2 : Athlétisme aux Jeux olympiques.
Le tableau ci-dessous donne des records olympiques féminins du 100
mètres depuis les Jeux
olympiques de 1952.
Année
|
1952
|
1960
|
1968
|
1976
|
1984
|
1992
|
2000
|
2008
|
2016
|
rang de l'année xi
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
temps ( s) yi
|
11,5
|
11
|
11
|
11,08
|
10,97
|
10,82
|
11,12
|
10,78
|
10,71
|
(source :Wikipédia)
2.1. Représenter dans le repère ci-dessous le nuage de points associé à
la série statistique (xi; yi).

2.2. Déterminer les coordonnées du point moyen G de ce nuage de points
et le placer.
Temps moyen =(11,5+11+11+11,08+10,97+10,82+11,12+10,78+10,71) / 9=10,997 ~ 11.
Une équaüon de la droite d'ajustement y en x obtenue par la méthode des
moindres carrés est:
y =- 0,064 x+ 11,254
2.3.1 Tracer cette droite dans le repère précédent.
2.3.2 A l'aide de cet ajustement, estimer le temps record du100 m
féminin qui pourrait être obtenu aux JO 2024.
x = 9 ; y = -0,064 x9 +11,254 ~10,68 s
2.3.3 Si la progression des athlètes continue de cette manière, à partir
de quelle année pourrait-on envisager un record du 100 m en dessous de la barre
des 10 secondes ?
- 0,064 x+ 11,254 < 10 ; 0,064 x > 1,254 ; x >19,6 soit 20 ( année 1952 + 20x8=2 112).
|
...
|
....
|
Exercice 3 : Préparation de soluüons
3,1. Nommez les instruments de laboratoire photographiés ci-dessous :
 I
I
3.2. Vous devez préparer une solution aqueuse par dilution. Quel
appareil de laboratoire est inutile parmi les appareils nommés ci-dessous ?
a-Pissette d'eau distillée ; b- poire à pipeter ; c- pipette jaugée ; d-fiole
jaugée.
e- balance ( inutile)
3.3. Vous préparez une soluüon aqueuse par dissolution d'une espèce
ionique dans de l'eau distillée. Classez les photographies illustrant le
protocole dans l'ordre chronologique :

Exercice 4- Réactions chimiques.
4.1.. Ecrire le bilan de réaction entre le dioxygène et le
dihydrogène.
O2(g) + 2H2(g) --> 2H2O(l).
4.2. On donne le schéma d'une pile dihydrogène-dioxygène alimentant un
moteur électrique. Précisez si les affirmaüons suivantes sont vraies ou
fausses :
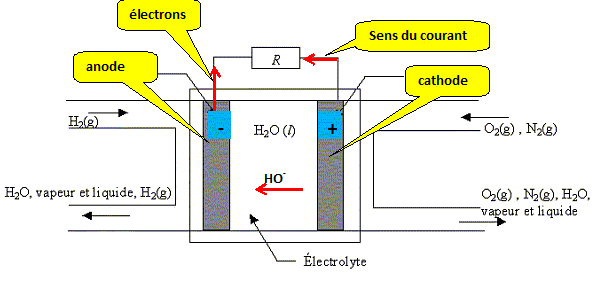
Affirmation a) Le sens conventionnel du courant électrique est de même
sens que le déplacement des électrons. Faux.
Affirmation b) L'électrode 1 ( arrivée de O2) est la borne + de cette pile. Vrai
Affirmation c) L'électrolyte est un solvant polaire. Vrai
4.3. La pile dispose initialement d'une réserve de 3,0 mol de O2 et de
4,0 mol de H2. Prévoir le réactif limitant lors de la décharge de cette pile.
3 mol de dihydrogène se combinent avec 1,5 mol de dioxygène. H2 est le réactif limitant.
4.4. Donner le schéma de Lewis des molécules O2, H2 et H2O.

Exercice 5. Élimination de l'organisme d'un médicament, le paracétamol.
Le paracétamol est une molécule uülisée pour ses propriétés
analgésiques.
On a modélisé ci-dessous la concentration en paracétamol dans le sang
humain, d'un volume total et constant de 5,0 L pour une prise répétée d'une même
quantité de 1 000 mg de paracétamol toutes les 6 heures. Le paracétamol est
naturellement éliminé, par transformation biochimique dans l'organisme, entre deux prises de
médicament.

D'après « GTICE académie de Lyon »
A0 est la concentration en paracétamol après la première prise de ce médicament.
5.1. Calculer la concentration en masse A en paracétamol dans le sang,
après la première prise de paracétamol, en supposant que l'absorption du
médicament dans sang est totale et immédiate.
1 / 5 = 0,2 g / L.
5.2. t0 est appelé « temps de demi-réaction ». Justifier cette appellaüon.
Durée au bout de laquelle la concentration initiale est divisée par 2.
5.3. A l'instant t0, on note la valeur de la concentration c0 =A0 / 2, et
à l'instant tn, cn=(cn-1+A0)/2.
Montrer l'expression suivante de cn et donner sa limite.
La concentration en paracétamol diminue d'un facteur 2 entre deux prises et augmente de A0 à chaque prise.
Au bout d'un temps suffisament long et avant chaque prise, la concentration tend vers zéro.
A t = t0, concentration c0=½A0 ; à t1= 2 t0, concentration c1=A0 +½ c0 = A0 +1/22 A0.
à t = 3 t0, concentration c2 =½c1 + A0 =½A0 +1/23 A0 +A0 .
à t = n t0, concentration cn =½cn-1 + A0 =1/2n-2A0 +1/2n A0 +A0 .
Exercice 6 : Dosage par titrage de l'acide aspartique.
L'acide aspartique, synthétisé en 1965 se retrouve dans l'édulcorant dit
« aspartame ».
on associe à cette espèce chimique les couples acido-basique suivants :
HOOC-CH(NH3+)-CH2-COOH / -OOC-CH(NH3+)-CH2-COOH pKa1 = 1,9.
-OOC-CH(NH3+)-CH2-COOH / -OOC-CH(NH3+)-CH2-COO- pKa2 = 3,6.
-OOC-CH(NH3+)-CH2-COO- / -OOC-CH(NH2)-CH2-COO- pKa3 =9,4
On prélève un volume Va=10 mL d'acide aspartique, sous sa forme la plus
acide
HOOC-CH(NH3+)-CH2-COOH , Cl- que l'on titre par de la soude Na+, HO- à la
concentration Cb=0,1 mol / L. En traçant la courbe V en fonction de pH, trois sauts de pH
sont identifiés dont le
deuxième, le plus net, est repéré pour un volume versé de soude de
volume Vbe = 20,0 mL.

6.1. L'acide aspartique est-elle une molécule chirale ? Justifier.
La molécule possède un atome de carbone asymétrique : cette molécule est chirale.
6.2. Justifiez la présence de 3 « sauts » de pH sur la courbe de
titrage,le premier et troisième « saut de pH » étant plus difficilement
discernables.
L'acide aspartique est un triacide, susceptible de céder 3 protons H+.
6.3. A l'issue du deuxième « saut de pH », le pH dans la soluüon est
alors voisin de pH = 8. Donnez la formule chimique de la molécule présente dans la
solution dont le pourcentage en espèce est noté (3) sur le graphique ci-dessus.
A pH un peu inférieur à pKa2, la forme -OOC-CH(NH3+)-CH2-COO- est majoritaire.
6.4. Déterminez la concentraüon en quantité de matière C en acide
aspartique de cette solution.
A la seconde équivalence : Cb Vbe = 2 C Va ; C = 0,1 x20 / (2x10) =0,1 mol / L.
SVT : la DMD.
Expliquer l'origine et la mise en place de la myopathie de Duchenne aux
différentes échelles et justifier qu'elle touche quasi-exclusivement
des garçons.
Cette maladie touche principalement les hommes. Ils ne possèdent qu'un
seul chromosome X, l'autre est un chromosome Y. Les individus sains ont
des enfants malades, l'allèle responsable est donc récessif.
La mutation d'un gène prive tout l'organisme de la protéine codée par
ce gène, protéine impliquée dans le soutien de la fibre musculaire.
Cette maladie est évolutive, elle provoque une dégénérescence
progressive de l'ensemble des muscles de l'organisme ( difficultés
motrices associée à une perte progreesive de la force musculaire, en
particuliers au niveau des membres inférieurs..
|
|