Physique,  Concours interne ingénieur industrie et des mines 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . .. .. .. ...... ... Exercice 1 (10 points) On essaye dans cet exercice de modéliser le trafic routier. On considère tout d’abord les véhicules individuellement. On note : xi : la position du véhicule i au temps t, vi sa vitesse et li sa longueur. si : l’espacement entre le véhicule 𝑖 et le véhicule devant lui (𝑖 – 1). gi : la distance au temps (t) entre le véhicule 𝑖 et le véhicule devant lui (𝑖 – 1). 1) Le modèle de Pipes (1953) considère que par sécurité la distance inter-véhicules doit être d'au moins la longueur d'une voiture pour chaque tranche de 16,1 km/h de vitesse du véhicule. Etablir la valeur minimum de gi en fonction de vi, li et vs où vs=16,1 km/h. Valeur minimale de gi : gi = li vi / vs. 2) On suppose maintenant que le nombre de voitures sur la route est constant, que tous les véhicules sont identiques de longueur L et qu’ils roulent à une vitesse moyenne v(x,t) dépendant de la densité linéique de véhicules K(x,t) (c’est-à-dire du nombre de véhicules par unité de longueur). L'espacement des véhicules peut donc être remplacé par l'inverse de la densité de la circulation. La densité maximum (Kmax) est atteinte lorsque les véhicules sont à l’arrêt pare-chocs contre pare-chocs. Donner l’expression de v(x,t) en fonction de K, Kmax et vs N : nombre de véhicules ; K =  v(x,t) = NL / t . gi = 1 / K =L v(x,t)/ vs. Kmax= 1 / L ; 1 / K = v(x,t)/ (vsKmax).. v(x,t) =vs Kmax / K. 3) On note N(x,t) le nombre de véhicules sur la route et Q(x,t) : le flux de véhicules en x à l’instant t. Donner la dimension de Q et établir une relation entre Q, K et v. Déterminer la valeur de K qui maximise Q. Q s'exprime en s-1. ( nombre de véhicules par seconde) . Q = N / t ;  K= N /x ; Q =Kx / t= K v(x,t). Qmax = Kmax v(x,t). 4) Le modèle LWR (développé par LightWill, Whitham, Richards) s’inspire ainsi de la mécanique des fluides et modélise le trafic routier comme un flux continu. On suppose maintenant que la vitesse varie linéairement entre 0 et une valeur vmax atteinte pour une densité K que l’on supposera nulle. Exprimer v en fonction de K, Kmax et vmax. v=vmax (1-K / Kmax). 5) La conservation du nombre de véhicules sur la route peut s’écrire : Q =K vmax(1-K / Kmax)= vmax ( K -K2/Kmax) ; puis dériver Q par rapport à x. 6) On pose : C(K)=v𝑚𝑎𝑥(1−2𝐾 / 𝐾𝑚𝑎𝑥) On cherche une ligne s(x,t), dite « caractéristique », le long de laquelle l’équation obtenue à la question (5) se réduit à une équation différentielle ordinaire : dK / ds=0 On rappelle que si K est une fonction composée plusieurs fois dérivable : Quelle est la forme d’une ligne caractéristique ? ... .... Exercice 2 (10 points) Le cycle à deux temps de Lenoir (1860) est un processus qui décrit le fonctionnement d'un moteur à combustion interne en deux phases principales : admission/compression et combustion/échappement. 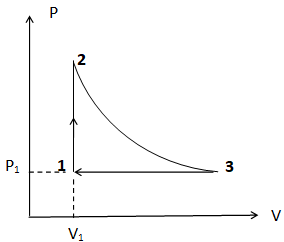Dans ce cycle, à partir d’un état initial (P1, V1, T1), un gaz parfait subit un échauffement isochore, puis une détente adiabatique et enfin un refroidissement isobare. On suppose que la variation du nombre de moles de gaz liée au carburant est négligeable et que le cycle est décrit de manière quasi-statique réversible. 1) Représenter le cycle de Lenoir dans un diagramme de Clapeyron. 2) On définit le taux de compression t comme le quotient du volume du cylindre lorsque le piston est au plus bas (volume maximal), par le volume lorsque le piston est au plus haut (volume minimal). On rappelle que le coefficient adiabatique g d’un gaz parfait est défini comme le rapport des capacités thermiques à pression constante (Cp) et à volume constant (Cv). On rappelle aussi que pour une transformation adiabatique réversible, la loi de Laplace peut s’écrire : TVg-1=constante. Déterminer le rendement h de ce cycle en fonction de t et g. Rendement du cycle = Travail total / chaleur absorbée = W23 +W31 / Q12. Processus isobare : T3 / T1 = V3 / V1. Processus adiabatique : T2 /T3 =(V3 / V1)g-1. Rendement = 1-Q31 / Q12 =1-g(T3-T1) /(T2-T1)=1-g(t-1) /(tg-1). 3) On pose t=2. Déterminer la température durant la détente et la pression maximum dans le cylindre. V3 = 2 V1 ; T3 = 2 T1 ; T2 /T3 =20,4=1,32. T2 =2,64 T1. P2V1 = n R T2 =2,64n R T1. 4) Exprimer le travail fourni au cours du cycle pour une mole de gaz en fonction de T1, P1 et R (constante universelle des gaz parfaits). W31= - P1(V3-V1)= -P1 V1 = -RT1. Adiabatique 2 3 : Q23 = 0 ; DU23 =W23= R(T3-T2)= R(2T1-2,64 T1) = -0,64 RT1. Dans le cycle de Beau de Rochas, également connu sous le nom de cycle à quatre temps, les quatre phases distinctes : admission, compression, combustion et échappement nécessitent quatre mouvements distincts du piston. En négligeant les phases d'admission et d'échappement, on peut modéliser le cycle par une série de transformations élémentaires : compression adiabatique, puis combustion isochore, détente adiabatique et enfin détente isochore. 5) Représenter ce cycle dans le diagramme de Clapeyron. Quelle est la principale différence entre le cycle de Lenoir et celui de Beau de Rochas ? 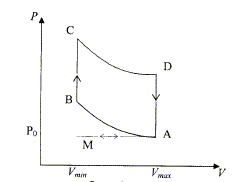Lenoir : moteur 2 temps ; Beau de Rochas : moteur à 4 temps. 6) Calculer le rendement pour ce cycle en fonction de t et g Commenter et comparer au rendement du moteur deux temps si l’on considère t =2 et g=1,4. Expression de Q1 quantité de chaleur échangée dans l'étape B-C : Q1 = nCvm( TC - TB ) avec ( TC - TB )>0 échauffement du gaz Q1 >0, chaleur reçue par le système, le gaz. Expression de Q2 quantité de chaleur échangée dans l'étape D-A : Q2 = nCvm( TA - TD ) avec ( TA - TD )<0 refroidissement du gaz Q2 <0, chaleur cédée par le système, le gaz. Expression du travail total W échangé au cours du cycle ABCD : l'énergie interne du gaz ne varie pas au cours du cycle : DU=0 Or DU=W+ Q1 +Q2 d'où W= -(Q1 +Q2) Expression de h en fonction de Q1 et Q2. efficacité ( rendement) : |travail fourni |/ énergie reçue à la source chaude ; h = |W|/Q1 = |-(Q1 +Q2)|/Q1 =|-(1+Q2/Q1 )| or Q1>0 et Q2<0 d'où h =1-|Q2| /Q1 expression de h en fonction de TA, TB, TC et TD : |Q2| /Q1 = | TA - TD | / ( TC - TB ) ; h = 1- | TA - TD | / ( TC - TB ) A-B adiabatique d'onc : TAVg-1maxi =TBVg-1mini (1) ; C-D adiabatique d'onc : TDVg-1maxi = TCVg-1mini (2) (1) -(2) donne : (TA - TD )Vg-1maxi = ( TB - TC )Vg-1mini ; (TA - TD )/ ( TB - TC ) = Vg-1mini / Vg-1maxi = (Vmini / Vmaxi)g-1 = t1-g h = 1- t1-g = 1-10-0,33 = 0,53. Rendement du cycle de Lenoir : 1-g(t-1) /(tg-1) =1-1,4 / (21,4-1)=0,15. ane.

menu