Physico-chimie
du corps humain : la vue. Concours général physique 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Formation
des images.
Oeil sain.
1. Déterminer la
distance focale du cristallin lorsque l'oeil regarde à l'infini.
La distance cristallin-rétine est égale à la distance focale de l'oeil
au repos ( objet situé à l'infini) soit 1,5 cm.
2. Faire de même
lorsque l'oeil regarde l'objet le plus proche ( situé à 25 cm environ)
qu'il peut voir net.
1 / fpp=1/mesure algébrique OA' -1 /mesure algébrique OA = 1
/ 0,015 - 1/(-0,25) =70,66 ; f pp= 1 / 70,66 ~0,014 m
(1,4 cm).
On considère que l'oeil est une sphère de rayon a et d'indice n. Un
rayon incident arrive sur l'oeil parallèlement à l'axe optique, avec
une hauteur h petite devant a. Il est réfracté et atteint la rétine en
son centre.
3.4. Evaluer
l'indice optique de la sphère pour que l'image d'un onjet à l'infini se
forme sur la rétine.
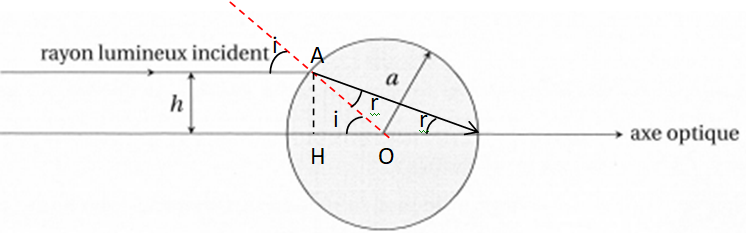
Loi de Descartes pour la réfraction : nair sin i = n sin r ;
sin i = n sin r ; n = sin i / sin r.
sin i = AH / OA = h / a ~ i si h << a.
tan r =AH / (OH +a) =h / (OH+a).
OH2 = a2 -h2 ; OH = a [ 1-(h / a)2]½
.
Si h << a : tan r ~ sin r et n ~(h / a) / (h
/(OH+a)]= 1+OH / a=1+ [ 1-h2
/ a2]½ ~1 +1-h2/(2a2)~ 2-h2/(2a2).
5.
Lorsqu'il se contracte, le cristallin modifie la courbure de la sphère
localement ( cela revient à modifier le rayon apparent de l'oeil
au niveau de l'entrée des rayons). Déterminer si pour voir de plus
près, le cristallin diminue ou augmente la rayon apparent de l'oeil
L'oeil doit réduire sa focale pour accomoder. Le rayon de courbure du
cristallin doit diminuer.
Correction d'un oeil myope.
6. Montrer
que deux lentilles minces accolées de distance focale respective f1
et
f2 sont équivalentes à une lentille mince de focale
telle que 1 /
f ' =1/ f '1 + 1/ f '2.
On note O le centre optique des deux lentilles , A la position de
l'objet, A'1 la position de l'image donnée par la lentille L1
et A'2 la position de l'image donnée par la
lentille L2.
A'1 joue le
rôle d'objet pour L2.
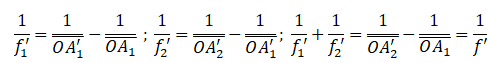
7. On considère un
oeil myope ( distance focale f m) : il voit au plus loin à
40 cm. Déterminer la valeur de la
distance focale ( fL) de la lentille de contact qui
permettra de corriger sa
vue.
L'oeil myope + lentille de contact doit être équivalent à l'oeil sain (
émmétrope) de focale 1,5 cm.
1 / f m + 1/fL = 1 / 0,015 =66,67 ; 1 / f m
= 1/ 0,015 -1/(-0,4)=69,17.
69,17+1 /fL = 66,67 ; 1 / fL = -2,5 ; fL = -0,4 m.
Les capteurs photosensibles ; cônes et
bâtonnets.
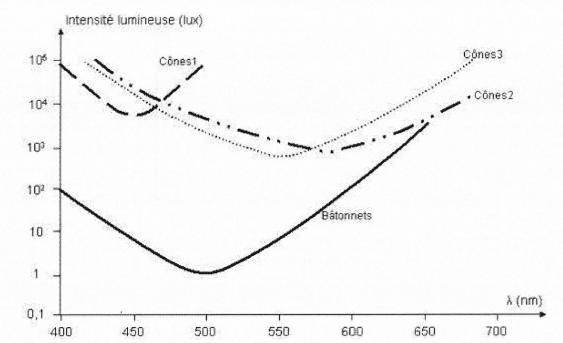
Le graphique suivant représente l'intensité lumineuse minimale pour
laquelle le photorécepteur réagit.
8. Justifier que
les bâtonnets sont associés à la vision nocturne.
Le
bâtonnets sont à peu près mille fois plus sensibles que les
cônes. Ils servent à la vision nocturne.
9. Identifier les
couleurs associées à chaque type de cônes.
10. A 550 nm, un éclairement de 1,0
W m-2 correspond à 683 lux. On donne le diamètre moyen de la
pupille de jour DP = 3,0 mm. Calculer la
puissance minimale en watt que doit recevoir l'oeil pour détecter un
rayonnement de longueur d'onde 550 nm.
Surface de l'oeil : 3,14 x (1,5 10-3)2 =
7,07 10-6 m2.
Intensité minimale pour activer les cônes : 103 lux soit 103
/ 683~1,46 W m-2.
Puissance = 1,46 x 7,07 10-6 ~ 1,1 10-5
W = 11 µW.
11. Calculer la
valeur du débit de photons.
Energie d'un photon E = h c / l
= 6,63 10-34 x 3 108 /(550 10-9)=3,6 10-19
J.
Débit : 1,1 10-5 / (3,6 10-19)=3 1013
photons / seconde.
|
...
|
....
|
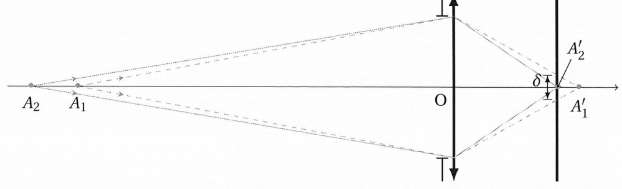
La mise au point est faite sur A2 dont l'image A'2
se forme exacrtement sur le capteur. L'image A'1 de A1
se forme plus loin de O sur le capteur. Les rayons issus de A1
forment donc sur le capteur une tache image de diamètre d. Ainsi tout point objet A1
sera vu net tant que d
< e où e est la taille
caractéristique du capteur ( on considère des capteur carré).
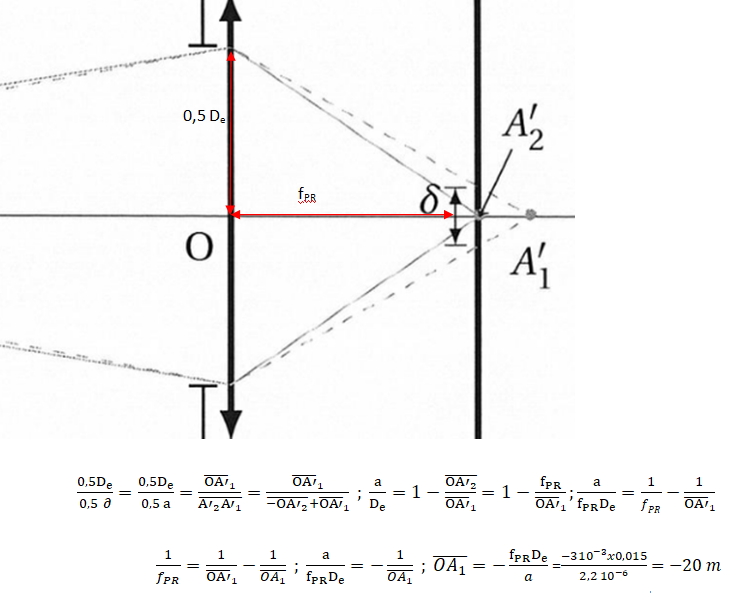
12. Sur la fovéa,
zone centrale de la rétine avec la plus grande densité de cones, il y a
en moyenne 2 105 cônes par mm2. On considére les
capteurs comme des carrés. Dans le cas d'un oeil qui n'accommode pas,
évaluer la distance à laquelle se situe l'objet le plus proche que
l'oeil voit net.
2 105 a2 = 10-6 ; a2 =5 1012
; a =2,2 10-6 m.
13. A l'aide d'un
schéma, montrer que si les capteurs ont une surface plus petite, on
diminue l'angle minimal du pouvoit séparateur.
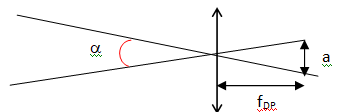
Si a diminue, alors a
diminue.
14. Montrer que la
valeur du pouvoir séparateur ( 3 10-4 rad) est cohérente
avec la densité de cônes dans la fovéa.
tan (0,5 a) ~0,5 a= 0,5 a / fPR.
a =
2,2 10-6 / (1,5 10-2) ~ 1,5 10-4 rad.
15. Nommer le
phénomène qui se manifeste lors du passage de la lumière à travers la
pupille de diamètre DP = 3 mm. En déduire pourquoi il n'est
pas utile de diminuer la surface des capteurs en deça d'une surface à
déterminer.
Diffraction de la lumière par la pupille. On note d le diamètre de la
tache.
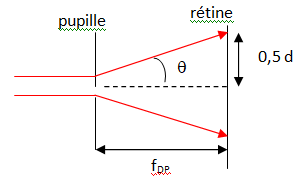
D'une part q = l / DP = 600 10-9
/ 0,003 = 2 10-4 rad ; d'autre part tan q~ q = 0,5 d / fDP ;
d = 2 q fDP
= 2 x 2 10-4 x 0,015=6 10-6 m.
Surface de la tache : p
( d / 2)2 =p
d2 / 4 =3,14 (6 10-6 )2/4=2,8 10-11
m2. |
|