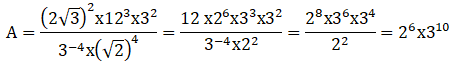
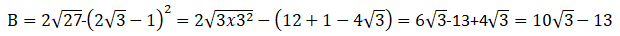
QCM mathématiques,  Concours Geipi polytech 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . .. . .. .. ...... ... La réponse proposée 310 x28 est fausse. La réponse proposée est vraie. C =ln(e /4) +ln(1 /(9e) +ln(36e) = ln[36e x e / (4 x9e)] =ln((e) = 1. La réponse proposée est vraie. D = exp(2ln3 +ln5)+exp(-2ln5) =exp(ln(3)2) x exp(ln 5)+exp(ln5-2)=9x 5 +exp(ln1/25))=45+1 / 25. La réponse proposée  20 est fausse. 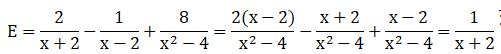Pour tout réel différent de -2 et de 2 : La réponse proposée est vraie. 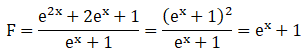La réponse proposée est vraie. Fonctions. A. La fonction f définie sur R* par f(x) =exp(1/x) admet pour dérivée f '(x) =exp(1/x). Faux. On pose u = 1 /x ; u' = -1/ x2 ; f '(u) = u' exp(u)  ; f '(x) = - 1 /x2  exp(1/x) . B- La fonction F définie sur [0 ; +oo[ par F(x) = x3/2 est une primitive de la fonction f définie par 1,5 x½. F '(x) = 3 / 2   x0,5 = f(x). Vrai. .C. La fonction  f  définie sur ]0 ; +oo[ par f(x)=(ln(3x))2 admet pour dérivée la fonction f '(x) = 2 ln(3x) / (3x). Faux. On pose u = ln(3x) ; u' = 3/(3x)= 1 / x ; f (u) =u2 ; f '(u) = 2 u u' ; f '(x) = 2 ln(3x)  / x. D. Quand x tend vers zéro, la limite de A =xln(x)-x est -oo. Faux. A=x(ln(x) -1).  ln(x) -1 tend vers -oo ; x tend vers zéro ; par produit des limites, A tend vers zéro. E. Quand x tend vers +oo, la limite de A = x ex-ln(x) est nulle. Faux. A = x[ex-ln(x) / x]. Par croissance comparée, en +oo : ln(x) / x tend vers zéro. ex tend vers plus l'infini. Par produit quand x tend vers +oo, A tend vers +oo. Soient f la fonction définie pour tout nombre réel x différent de 1 par f(x) = 3 /(1-x) et Cf sa courbe représentative dans un repère orthonormé. Quand x tend vers 1-,  f(x) tend vers -oo. Faux. 1-x tend vers 0+ et f(x) tend vers +oo.  Une équation de la tangente à la courbe Cf au point d’abscisse x = −1 est y = 3 /4 x+½ . Faux. f '(x) = 3 /(1-x)2. f '(-1) = 3 / 4. Equation de la tangente : y = 3 /4 x +b. Le point de coordonnées (-1 ; f(-1) =1,5) appartient à la tangente : 1,5 = -0,75 +b ; b = 2,25 =9/4. y = 0,75 x +9/4. f est concave sur ]1 ; +∞[. Vrai. On pose u =1-x ; f '(u) = 3 u-2 ; f "(u) = -6 u' u-3 ; f "(x) =6 /(1-x)3. f "(x) < 0 sur ]1 ; +∞[. ... .... Suites. Soit (un) une suite telle que un ≠ 0 pour tout entier naturel n. Pour tout entier naturel n, on définit la suite (vn) par vn = − 2 / un . A- Si (un) est minorée par 2, alors (vn) est minorée par −1. Vrai  un > 2 ; 2 / un < 1 ; -2 / un > -1. B- Si (un) est croissante, alors (vn) est décroissante. Faux. La suite définie par un = n+ 1 est croissante. La suite vn = -2 /(n+1) est également croissante. C- Si (un) converge, alors (vn) converge. Faux. La suite définie par un = 1 /(n+1) converge vers zéro. vn = -2 (n+1) diverge vers -oo. Probabilités.  On lance cinq fois un dé à six faces. Cocher VRAI si la variable aléatoire proposée suit une loi binomiale et FAUX dans le cas contraire. A- La variable aléatoire correspondant au nombre de lancers où apparait un numéro pair. Vrai.  B- La variable aléatoire correspondant à la somme des résultats de tous les lancers.  Faux. W désigne l’univers d’une expérience aléatoire E et P désigne une probabilité sur W. A et B sont deux événements de probabilités respectives 0,6 et 0,4. On suppose de plus que P(A u B) = 0,8. A- P(A ∩ B) = 0,24. Faux. P(A ∩ B) = P(A) +P(B) - P(A u B) =0,6 +0,4 -0,8 = 0,2. B- A et B sont des événements contraires. Faux. Si A et B sont des événements contraires, alors ils sont incompatibles et P(A u B) =1  C- A et B sont des événements indépendants. Faux. Pour deux événements indépendants P(A n B) = P(A) x P(B), ce qui n'est pas le cas. D- A et B sont des événements incompatibles. Faux. Pour deux événements incompatibles P(A n B) = 0, ce qui n'est pas le cas.  Géométrie dans le plan .  On considère les points A et B de coordonnées respectives dans un repère orthonormé : A(2 ; 0) et B(0 ; −4) .  A- Une équation de la droite (AB) est 2x − y − 4 = 0. Vrai. Si A appartient à cette droite : 2 *2-0-4 =0 vrai. Si B appartient à cette droite : 2 *0-(-4) -4 =0 vrai. B- Une équation de la médiatrice du segment [AB] est x + 2y + 3 = 0. Vrai. Coordonnées du milieu I du segment [AB] : 1 ; -2. Soit M(x ; y) un point de la médiatrice.  C- Une équation du cercle de diamètre [AB] est 𝑥2 + 𝑦2 − 2x − 4x𝑦 = 0. Faux. Coordonnées du milieu I de [AB], centre du cercle : 1 ; -2. Rayon du cercle ½AB = R =½(22 +(-4)2)½ =5½. Equation du cercle : (x-xI)2 +(y-yI)2 = R2. (x-1)2 +(y+2)2 =5 ; x2-2x+1+y2+4y+4 =5 ; x2-2x+y2+4y =0.  D- Le point de coordonnées (−1 ; −1) appartient au cercle de diamètre [AB]. Vrai. Si I appartient à ce cercle : (-1)2+(-1)2 -2(-1)+4(-1) =0 est vérifié. E- La droite d’équation 2𝑥 − 𝑦 + 1 = 0 est tangente au cercle de diamètre [AB]. Vrai. Si cette hypothèse est vraie : la droite et le cercle ont un seul point commun. y = 2x+1 ; x2-2x+y2+4y =0. x2-2x+(2x+1)2+4(2x+1) =0. Cette équation soit admettre une seule solution. 5x2+10x+5=0 ; x2+2x+1=0 ; (x+1)2=0 soit x=-1, seule solution.

menu