Diffraction, interférences, Concours Geipi polytech 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... La microfiltration des eaux usées représente de nos jours un enjeu sanitaire et écologique majeur. Le liquide à dépolluer s’écoule dans des membranes microporeuses. Pour simplifier, on peut considérer qu’une membrane est une plaque percée de trous circulaires de diamètre a et espacés les uns des autres d’une distance b. On se propose ici de déterminer expérimentalement a et b par un dispositif optique mettant en jeu les phénomènes de diffraction et d’interférences de la lumière. Partie 1 : Questions préliminaires. Un laser produisant une radiation électromagnétique monochromatique de longueur d’onde l = 500 nm est utilisé dans le dispositif optique. I-1- Donner l’expression littérale reliant la fréquence f et l. En déduire la valeur numérique de f. l = c / f ; f = 3,0 108 / (500 10-9)=6,0 1014 Hz.  I-2- Terminer la phrase suivante:  « Les expériences de diffraction et d’interférences apportent la preuve que la lumière a une nature ondulatoire »  Partie 2 : Diffraction. 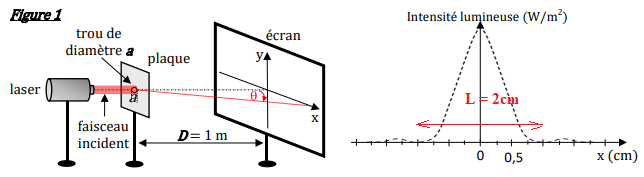On éclaire un trou circulaire de diamètre a par le laser selon le protocole expérimental décrit sur la figure 1. Un phénomène de diffraction se produit. La figure de diffraction est observée sur un écran placé à une distance D de la plaque percée. Dans le cas de la diffraction par un trou circulaire, l’écart angulaire de diffraction q a pour expression littérale : q = 1,2 l / a . 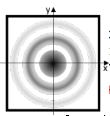I-3- Parmi les exemples de figures de diffraction proposées, choisir celle correspondant à la diffraction obtenue avec un trou circulaire.  I-4- Le graphique de la figure 1 représente les variations de l’intensité lumineuse mesurées sur l’écran en fonction de l’axe x. Donner la valeur numérique de la largeur L de la tache centrale. L = 2 cm. I-5- En faisant l’approximation des petits angles (q~L /(2D) ), donner l’expression littérale du diamètre du trou circulaire a en fonction de l, D et L. En déduire sa valeur numérique. q =1,2 l / a = L/(2D) ; a = 2,4 l D / L=2,4 x500 10-9 x1 / 0,02=6,0 10-5 m. ... .... Partie 3 : Interférences.  On éclaire deux trous circulaires de diamètre a et séparés par la distance b selon le protocole expérimental décrit à la figure 2. En plus du phénomène de diffraction, un phénomène d’interférences se produit également. La figure d’interférences s’observe sur l’écran. I-6- Parmi les exemples de figures d’interférences proposées, choisir celle correspondant aux interférences obtenues avec des trous circulaires (cas des trous d’Young).  I-7- Le graphique de la figure 2 représente les variations de l’intensité lumineuse mesurées sur l’écran en fonction de l’axe x. Donner la valeur numérique de l’interfrange i. i = 2 / 5 =0,4 cm.  I-8- A partir d’une analyse dimensionnelle, choisir  l’expression littérale liant l’espacement b entre les deux trous, λ, D et i . En déduire la valeur numérique de l’espacement b.  i = l D / b ; l, D, b et i s'expriment en mètre ; l D s'exprime en m2 ;  l D / b s'exprime en mètre. b =  l D / i =500 10-9 x1 / (4 10-3)=1,25 10-4 m.

menu