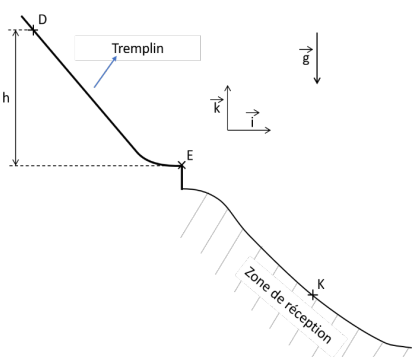
Au cours d’une épreuve de saut à ski, le skieur
démarre sa prise d’élan sur un tremplin au point D pour prendre son
envol au point E, à l’extrémité inférieure du
tremplin. Pour ne pas être pénalisé sur la note
de saut, le sportif doit atterrir au point K, ou
plus loin dans la zone de réception. La hauteur
du tremplin est notée h.
On assimilera le skieur à un point G qui se
déplace le long du tremplin pendant la prise
d’élan, puis dans l’air au cours du vol ; sa
masse est m = 50 kg. g = 10 m s
-2.
 Partie 1 : Prise d’élan sur le tremplin
Partie 1 : Prise d’élan sur le tremplin.
Le départ s’effectue sans vitesse initiale ; la vitesse du skieur au point d’envol E est notée V
E. Les
frottements avec l’air et la piste sont négligés : le skieur n’est soumis qu’à son poids et à la réaction
normale de la piste.
III-1- Exprimer la variation d’énergie potentielle de pesanteur du skieur entre les points D et E,
en fonction des paramètres pertinents parmi g, h, m, V
E.
DEp = -mgh.
III-2- Exprimer variation d’énergie cinétique du skieur entre D et E en fonction des paramètres
pertinents parmi g, h, m, V
E.
DEc = ½mv
E2.
III-3- En appliquant la conservation de l’énergie mécanique, donner l’expression de la vitesse V
E
en fonction des paramètres pertinents parmi m, g et h. Faire l’application numérique pour h = 45 m.
La variation d'énergie cinétique est égale au travail moteur du poids :
½mvE2 = mgh.
VE = (2gh)½ =( 2 x10 x45)½ =900½ = 30 m /s.