Corpuscule dans le champ de pesanteur, Concours ENAC 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Dans le référentiel galiléen du laboratoire supposé galiléen, un projectile A assimilé à un corpuscule (i.e. point matériel), est tiréà l’instant initial dans un plan vertical Pv depuis l’origine O d’un repère cartésien. Le vecteur vitesse initiale v0 forme un angle q avec l’axe horizontal. g ≈ 10 m. s-2. On néglige tout frottement. On considère une cible C placée à la distance d et à une hauteur h, dans Pv. 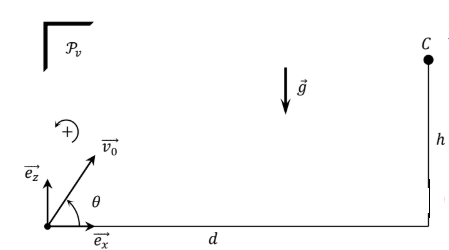1. Quelle condition doivent satisfaire v0 et q pour que l’altitude maximale, hM, atteinte par A vérifie hM > h ? Travail de la seule force, le poids, entre l'altitude de départ et hM : W = -mghM. Lorsque l'amtitude maximale est atteinte, la composante verticale de la vitesse est nulle. Composante horizontale de la vitesse : v0 cos q. Variation de l'énergie cinétique : ½m(v0 cos q)2-½mv02=½mv02(cos q2-1)= -½mv02 sin q2). Théorème de l'énergie cinétique : -½mv02 sin q2 =-mghM. hM = ½v02 sin q2 / g. v0 sin q > (2gh)½. 2. Quelle relation v0 et q doivent-ils satisfaire pour que la cible soit atteinte ? Composantes de la vitesse : v0 cos q ; -gt+ v0 sin q t. Par intégration : x = v0 cos q t ; z = -½gt2 + v0 sin q t. Trajectoire : t = x / v0 cos q ; z = -½g(x / v0 cos q )2 + x tan q. h = -½g(d / v0 cos q )2 + d tan q .  3. On fixe v0 (jusqu’à la fin de cet exercice), q devenant alors le seul paramètre variable. La cible n’est atteinte que lorsque : K1tan2 q − d tan q + K2 = 0 où K1 et K2 sont des coefficients indépendants de q. Exprimer K1 et K2. tan2 q =(1-cos2 q) / cos2q  =1/ cos2q-1. 1/ cos2q =1+tan2 q . h = -½gd2 / v02(1+tan2 q) + d tan q. ½gd2 / v02tan2 q - d tan q.+h +½gd2 / v02=0. On identifie : K1 = ½gd2 / v02 ; K2 = h +½gd2 / v02. ... .... 4. La cible peut être atteinte si son altitude h ne dépasse pas une altitude limite hl(d, v0). Exprimer hl(d, v0). K1tan2 q − d tan q + K2 = 0 Le discriminant doit être positif ou nul : d2-4K2 K1 > 0. d2 -4( h +½gd2 / v02.)  (½gd2 / v02)> 0. d2 -2 hgd2 / v02 -g2d4 / v04.> 0. 1 -2 hg / v02 -g2d2 / v04.> 0. 1-g2d2 / v04.>2 hg / v02 . v02 -g2d2/ v02>2 hg . h <  v02 / 2g-½gd2/ v02. hl =  v02 / 2g-½gd2/ v02. 5. La condition précédente étant respectée, combien de trajectoires contiennent la cible ? Si l'angle q appartient à [0 ; ½p] et si la condition précédente est respectée, l'équation admet 2 solutions donc deux trajectoires possibles ( discriminant positif) ou une seule solution donc une seule trajectoire si le discriminant est nul. ane.

menu