Physique des océans.
Concours EMIA 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
La houle.
On modélise l'entrée d'un port par une ouverture de largeur a. La
houle est assimilée à une onde mécanique progressive sinusoïdale
arrivant vers le port. Elle soilève de façon périodique le petit bateau
situé au large. La célérité c de cette onde dépend de la
profondeur d'eau h et de g = 9,81 m s-2.
Cas a : si h est très grande devant la longueur d'onde l : c = (gl/ (2p)½.
Cas b : h est faible c = (gh)½.
1.1- La houle est-elle une onde mécanique longitudinale ou transversale ?
La déformation du milieu est perpendiculaire à la direction de propagation : onde transversale.
1.2 Justifier que (gh)½ est homogène à une vitesse. g s'exprime en m s-2 et h en m : gh s'exprime en m2 s-2.
(gh)½ s'exprime en m s-1.
1.3. Exprimer en fonction de la fréquence f, la célérité de la houle.
f =c / l ; l = c / f ; cas a : c2 = gl/ (2p) =cg / (2 f p) ; c = g / (2 f p).
Cas b : c = gh, indépendant de la fréquence.
1.4. Dans quel cas le milieu est-il dispersif ? Dans ce cas comment varie la célérité si la fréquence double ?
Dans un milieu dispersif, la célérité dépend de la fréquence ( cas a).
Si la fréquence double, la célérité est divisée par 2.
Le petit bateau de pêche est en mer au large du port. La profondeur hest égale à 800 m et la longueur d'onde de la houle est l = 50 m.
1.5 Calculer la célérité de cette onde.
c = (gl/ (2p)½= (9,81 x50 / 6,28)½ =8,8 m /s.
1.6. Calculer la fréquence du mouvement vertical du bateau.
f = c / l = 8,8 / 50 ~0,18 Hz.
Près de la côte.
La profondeur est faible devant la longueur d'onde.
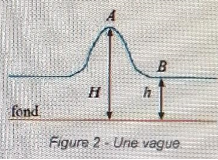
1.7. Exprimer les célérité cA au point A et cB au point B. Laquelle est la plus grande ?
cB = (gh)½ ; cA = (gH)½ ; H > h donc cA > cB.
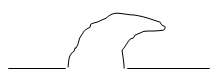
1.8. En déduire que cette vague se déorme et représenter sur un schéma simple son allure quelques instant plus tard.
La célérité en haut de la vague est supérieure à la célérité à sa base : la vague se déforme, elle bascule.
A l'entrée du port.
h = 2,5 m; a = 25 m. On observe un phénomène de diffraction par l'ouverture.
1.9. Donner un ordre de grandeur de la longueur d'onde de la houle susceptible d'être diffractée par cette ouverture.
L'onde étant difractée par cette ouverture, la longueur d'onde est du
même ordre de grandeur que la dimension de l'ouverture soit 25 m.
1.10. Calculer la célérité de cette onde.
c = (gh)½=(9,81 x 2,5)½ ~5,0 m/s.
1.11. Sur un schéma
simplifié, représenter en vue de dessus, l'entrée du port, la houle
incidente et l'onde diffractée. Quelle est la forme des ondes avant et
après diffraction ?
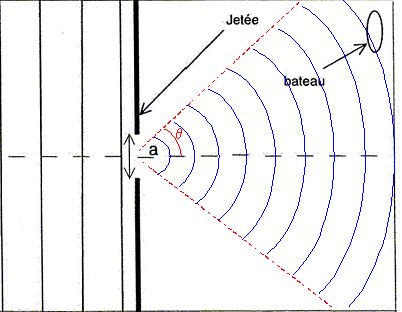
La longueur d'onde des ondes reste inchangée.
Plongeon.
On étudie le mouvement d'un baigneur de masse m = 80 kg
qui saute d'un plongeoir situé à une hauteur h = 10 m au dessus de la
surface de l'eau. Il se laisse chuter sans vitesse initiale et il est
soumis uniquement à la pesanteur durant sa chute.
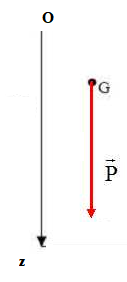
2.1 Faire un schéma de la situation.
2.2. Déterminer, la conservation de l'énergie mécanique, la vitesse v0 d'entrée dans l'eau.
L'énergie mécanique initiale est sous forme d'énergie potentielle de pesanteur : mg h.
L'énergie mécanique finale est sous forme cinétique : ½mv02.
L'énergie mécanique se conserve : ½mv02= mgh ; v02=2gh = 2 x9,81 x10 =196,2 ; v0 =14 m/s.
Lorsqu'il est dans l'eau il ne fait aucun mouvement. Il subit en plus de la pesanteur :
une force de frottement f = kv avec k = 250 kg s-1.
la poussée d'Archimède.
Densité du corps humain d = 0,9. On note Oz l'axe vertical descendant,
O est le point de la surface de l'eau et t=0 l'instant ou le baigneur
rentre dans l'eau.
2.3. Exprimer la poussée en fonction de m, d et g.
Volume du baigneur : V = m / rcorps ; d = rcorps / reau ; V = m / (d reau ).
Poussée = F= poids du volume d''eau déplacé = V reau g = mg /d.
2.4 Etablir l'équation différentielle à laquelle obéit la vitesse v en projection sur l'axe Oz.
On posera t = m / k = 80 / 250=0,32 s.
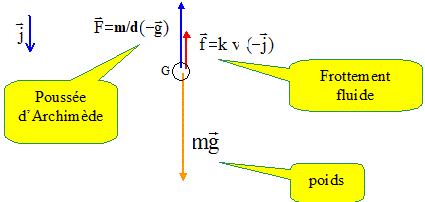
Ecrire la seconde loi de Newton projetée sur l'axe vertical descendant :
mg -kv-mg /d = mdv/dt ; g -k/ m v-g /d = dv/dt ;
dv/dt +k /m v = g(1-1/d) ; dv/dt +1 / t v = g(1-1/d).
2.5. Déterminer la vitesse limite atteinte.
dvlim /dt = 0 ; 1 / t vlim = g(1-1/d).
vlim = g(1-1/d) t =9,81(1-1/0,9) x0,32 ~-0,35 m/s.
La vitesse limite est dirigé vers le haut : vitesse limite de remontée du plongeur.
2.6 Résoudre l'équation et exprimer v(t) en fonction de v0, vlim, t et du temps.
Solution générale de l'équation sans second membre : v = A exp(-t / t) avec A une constante.
Solution particulière ; vlim.
Solution générale : v = A exp(-t / t) + vlim.
A t=0 : v0 =A + vlim ; A = v0 -vlim.
v = (v0 -vlim) exp(-t / t) + vlim.
2.7 A quel instant le baigneur commence t-il à remonter ?
A l'instant ou il commence à remonter v = 0.
(v0 -vlim) exp(-t / t) + vlim = 0 ; exp(-t / t) = -vlim / (v0 -vlim) = 0,35 /(14+0,35)~0,0244.
-t / t = ln(0,0,044) =-3,71 ; t = 3,71 x0,32 ~1,2 s.
2.8 Déterminer la profondeur maximale atteinte.
Position = primitive de la vitesse : z = -(v0 -vlim) t exp(-t / t) + vlim t + cste.
A t=0, z = 0 : 0 = -(v0 -vlim) t + Cste ; Cste = (v0 -vlim) t = 14,35 x0,32~4,6 m.
zmaxi = -(14+0,35) x0,32 exp(-1,2 /0,32) -0,35 x1,2 +4 6= 0,74 m.
3. Magnétisme océanique.
Quand
l'eau de mer se déplace dans le champ magnétique terrestre, elle se
retrouve parcourue par un courant électrique qui génère une force
magnétique.
|
...
|
....
|
Exercice 4. Modèle du poisson électrique.
4.1. Quand la raie n'est pas active, le potentiel d'action est nul, ce
qui revient à laisser l'interrupteur I ouvert. Quelle est alors la
tension aux bornes de l'électroplaque ?
La
tension aux bornes de l'électroplaque est nulle.
4.2 Le cerveau de la raie active l'électroplaque en commandant la
fermeture de l'interrupteur. Préciser la tension aux bornes de
l'électroplaque.
La
tension aux bornes de l'électroplaque est égale à la tension aux bornes du générateur.
4.3 Montrer que deux générateurs électriques, identiques de tension e
et de résistance interne r, mis en série, sont équivalents à un
générateur de tension 2e et de résistance interne 2r. On fera un schéma.
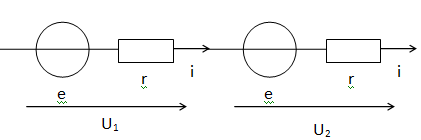
U1 =U2 = e-ri ; U1+U2 = e-ri+e-ri = 2e-2r i.
4.4. En déduire le nombre d'électroplaques empilées pour arriver à une
tension de 70 V. Comment estimer le courant maximal de 7 mA
indiqué.
4.5 Les piles d'électroplaques sont-elles placées en série ou en parallèle pour augmenter le courant ? Justifier.
En associant les piles en parallèle, les intensités dans chaque branche s'ajoutent.
4.6 Calculer la puissance d'une impulsion de raie de 70 V et 30 A. Quelle est l'énergie déployée si celle-ci dure 10 ms.
Puissance (watt) = tension (V) x intensité (A) = 70 x30 = 2,1 103 W.
Energie (joule) = puissance (watt) x durée (seconde) = 2,1 103 x0,01 =21 J.
Chasse à la raie.
4.7 Rappeler la loi de Descartes pour la réfraction.
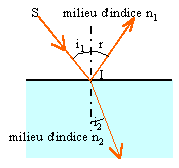
Les trois rayons incident, réfléchi et
réfracté sont dans le même plan ;
l'angle d'incidence i1 est égal à
l'angle de réflexion r. Les angles d'incidence
i1 et réfracté i2 sont
reliés par la relation : n1 sin
i1 = n2 sin
i2
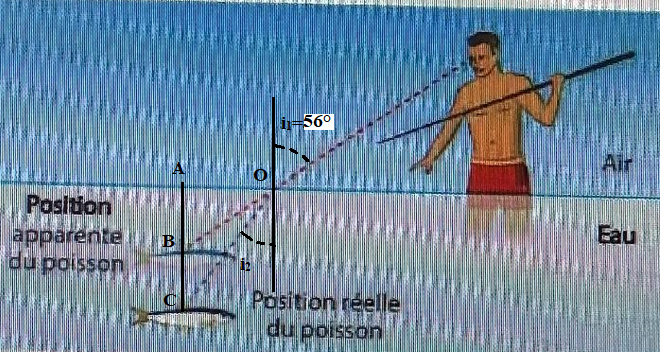
4.8 Calculer numériquement l'angle de sortie du rayon lumineux venant du poisson, en considérons que la figure est à l'échelle.
i1 ~56 degrés mesurés au rapporteur.
4.9 Appliquer la loi de Descartes pour calculer la différence d'angle
entre la direction apparente du poisson et sa direction réelle. n1 = 1,33 pour l'eau et n2 = 1 pour l'air.
neau sin i2 = nair sin 56 ; sin i2 = sin 56 x 1 / 1,33~ 39°.
56-39 = 17°.
4.10. Le pécheur voit l'image du poisson à une profondeur AB=h = 50 cm. Calculer la profondeur du poisson réel.
tan (90-56)= tan 34= AB / AO ; tan(90-i2) = tan 51 =AC / AO ; AC = AB tan 51 / tan 34 ~92 cm.
Exercice 5 : du deutérium pour la fusion nucléaire.
Une centrale à fusion aurait besoin de 100 kg de deutérium et 3 tonnes
de lithium pour fonctionner pendant une année et produit de l'hélium,
gaz neutre, non polluant.
Le deutérium se trouve à l'état naturel dans l'eau de mer (33 g / m3) et le tritium peut être fabriqué à partir du lithium de la croûte terrestre..
m(12H) = 2,01355 u ; m(13H) = 3,01550 u ; m(24He) = 4,00150 u ; m(01n) = 1,00866 u ; 1u =1,66 10-27 kg.
1. Quel volume d'eau de mer doit-on traiter pour récupérer 100 kg de deutérium ?
100 / 0,033 ~3,0 103 m3.
2. Définir isotopes. Quelle est la composition des noyaux de deutérium, de tritium ?
Deux isotpes ne diffèrent que par leur nombre de neutons. Ils possèdent le même numéro atomique Z.
Deutérium : 1 proton et un neutron ; tritium : 1 proton et deux neutrons.
3. Le graphe ci-dessous présente l'opposée de l'énergie de liaison par nucléon -El / A en fonction du nombre de nucléon. Cette grandeur représente l'énergie de cohésion du noyau.
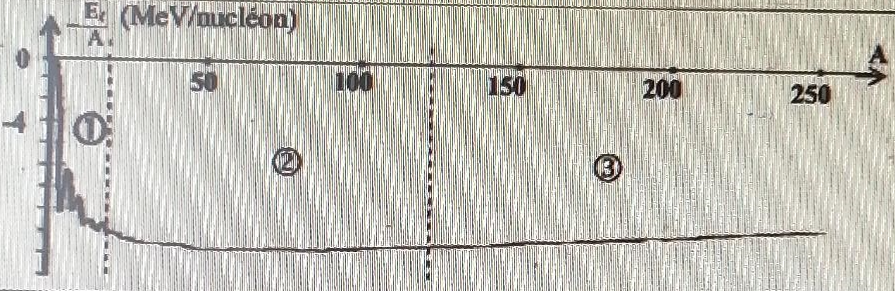
Dans quel domaine
( 1, 2 ou 3) les noyaux sont'ils susceptibles de subir des réactions de
fusion ? de fission ? Donner un ordre de grandeur de A
pour le noyau le plus stable.
1 : réaction de fusion ; 3 : réaction de fission. Pour les noyaux les plus stables A ~ 50.
4. Ecrire et équilibrer l'équation de fusion entre le deutérium et le tritium.Quelle règle est utilisée ?
31H + 21H --> 42He +10n.
Conservation du nombre de nucléons : 3+2 = 4+1.
Conservation de la charge : 1 +1 = 2 +0.
5.
Calculer en joules l'énergie produite pendant 1 an de fonctionnement
d'une centrale de fusion avec 100 kg de deutérium. Comparer à l'énergie
produite pendant la même durée par un réacteur actuel de puisance 900
MW.
Dm = m(10n) +m(42He) -m(21H) -m(31H)
Dm =4,00150 + 1,00866-3,01550-2,01355 = -1,889 10-2 u.
1,889 10-2 * 1,66054 10-27 = -3,13676 10-29 kg.
Energie =E =| Dm | c2 = 3,13676 10-29 *( 2,998 108 )2 = 2,81932 10-12 J.
Soit pour 100 kg de deutérium et la quantité nécessaire de tritium :
masse d'un noyau de deutérium : 2,01355 *1,66 10-27 =3,34 10-27 kg.
Nombre de noyaux de deutérium dans 100 kg : 100 / (3,34 10-27)~3 1028 noyaux.
2,81 10-12 x 3 1028 =8,4 1016 J.
Réacteur actuel : puissance (watt) * durée (s) = 9 x 108 x(365 x24 x3600)=2,8 1016 J ( 3 fois moins que le réacteur de fusion).
|
|