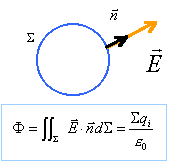Physique,
Concours EMIA 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
A. Eclairage de la salle, tube fluo.
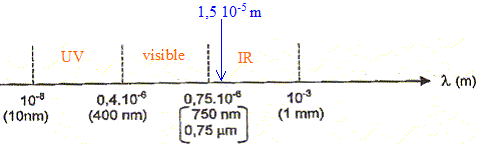
1. Placer
sur un diagramme les domaines des rayons infrarouge ( iR) et des
ultra-violets ( UV). Préciser les longueurs d'onde des différentes
frontières.
 2.1. A quelle force est soumis un électron plongé dans un champ électrique ? Donner le nom et l'expression de cette force.
2.1. A quelle force est soumis un électron plongé dans un champ électrique ? Donner le nom et l'expression de cette force.
Les
électrons sont soumis à une force électrique F colinéaire au champ
électrique E mais de sens contraire ( la charge est négative). norme
(F) = e x norme (E)
2.2.
Quelle est la valeur du champ électrique E créé par deux éléctrodes
distantes de d = 60 cm et soumises à une tension U = 20 V ?
E = U / d = 20 /0,6 ~33 V m-1.
2.3. Quelle est la vitesse atteinte par un électron après la traversée du tube fluo, en le supposant initialement au repos ?
e = -1,6 10-19 C ; m = 1,67 10-27 kg.
Théorème de l'énergie cinétique : ½mv2 -0= |e| U, travail de la force électrique.
v2 = 2 |e|U / m =2 x1,6 10-19 x 20 / (1,67 10-27) =3,8 109 ; v = 6,2 104 m /s.
=
3. Le mercure de symbole Hg a pour numéro atomique Z = 80 et possède au moins 40 isotopes stables.
3.1. Définir isotope.
Deux isotopes ne diffèrent que par leur nombre de neutrons. Ils possèdent le même numéro atomique Z.
3.2. Quelle est la composition du noyau de mercure 202 ?
80 protons et 202-80 =122 neutrons.
3.3 Le mercure 203 est radioactif ß- de demi-vie T = 46,7 jours. Ecrire l'équation de désintégration.
20380Hg -->20381Tl ( Thalium)+ 0-1e (électron).
3.4. Que représente la demi-vie du mercure 203 ?
La demi-vie est la durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.
B. Utilisation d'un néon
Un néon ne s'allume que si la tension entre ses bornes atteint Va = 228 V. Il reste allumé tant que la tension à ses bornes est
supérieure à Ve = 218 V.. Le néon éteint se comporte comme un
interrupteur ouvert. Allumé il peut être modélisé par une résistance r
= 10 kW.
1. Que vaut l'intensité I lorsque le néon est éteint ?
I = 0.
2. Quelle est la relation entre la tension U à ses bornes et l'intensité lorsque le néon est allumé ?
Loi d'Ohm U = r I.
3. On souhaite tracer la courbe I = f (U)
3.1. Calculer les courants Ia et Ie correspondants aux potentiels d'allumage et d'extinction.
Ia = Ua / r = 228 / 104 =2,28 10-2 A=22,8 mA.
Ie = Ue / r = 218 / 104 =2,18 10-2 A=21,8 mA.
3.2. On part d'une tension nulle aux bornes du néon qu'on augmente peu à peu. Que se passe t-il quand U = Ua?
Le néon s'allume.
3.3. On continue à augmenter U au delà de Ve puis on la diminue. Que se passe t-il quand on arrive à U = Ve ?
Le néon s'éteint.
3.4. Représenter la caractéristique I = f(U).
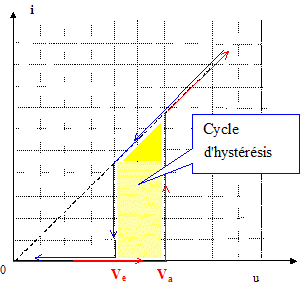
Dans le cycle d'hystérésis le néon est allumé.
4. Le néon est-il un dipôle actif ou passif ?
Dipôle passif : hors d'un circuit électrique, la tension aux bornes du néon est nulle.
5. On considère le
circuit ci-dessous. Le néon est mis en parallèle avec le
condensateur. A t = 0 le condensateur est déchargé et le néon est
étteint.
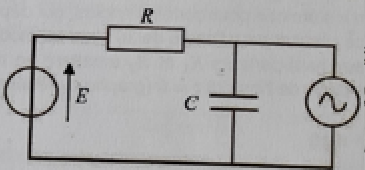
5.1. Etablir l'équation différentielle de la tension u(t) et la résoudre.
Additivité des tensions : E = R i + u(t).
i = dq/dt = C du(t) /dt.
E = RC du(t) /dt + u(t).
Solution générale de l'équation sans second membre : u(t) = A exp(-t /(RC)) avec A une constante.
Solution particulière de cette équation : u(t=0) = E.
Solution générale : u(t) =A exp(-t /(RC))+E.
A t =0, u(t) = 0 ;0 = A + E ; A = -E.
u(t) =-E exp(-t /(RC))+ E= E(1-exp(-t /(RC))).
5.2 A quelle condition le néon s'allume t-il ? Cette condition étant respectée, donner l'expression du temps t1 au bout duquel il s'allume.
Le néon s'allume si u(t) atteint la valeur Ua.
Ua = E(1-exp(-t1 /(RC))).
Ua / E =1-exp(-t1 /(RC)).
1-Ua / E =exp(-t1 /(RC)).
ln(1-Ua / E)=-t1 /(RC).
ln(1/(1-Ua / E))= t1 /(RC).
t1 = RC ln(1/(1-Ua / E)).
|
...
|
....
|
1. Donner la valeur de la célérité du son dans l'air.
2. Le son est-il une onde transversale ou longitudinale ? Comment est-il produit ?
Le son est une onde longitudinale.
Le son est produit par la vibration d'un corps solide, liquide ou gazeux qui constitue la source sonore.
3. Le son émis est un "la" de fréquence f = 440 Hz.
3.1 Relation entre longueur d'onde l et fréquence :
l = c / f avec c : célérité.
l = 340 / 440 ~0,77 m.
Cette onde peut être diffractée par un obstable de dimension voisine de 0,77 m, pilier ou porte.
4.
On utilise une paire de haut-parleurs H1 et H2 disposés à une distance
a = 3 m l'un de l'autre. Le système est testé pour des sons de
fréquences différentes en mesurant l'intensité du son en fonction de
l'angle q sur un arc de cercle OM = 3 m.
On remarque que le son "s'éteint" pour certains angles qui dépendent de
la fréquence. On essaie de retrouver ce résultat pour l'angle de 30°.
Les deux haut-parleurs émettent en même temps un son de fréquence f = 100 Hz à partir de l'instant t = 0.
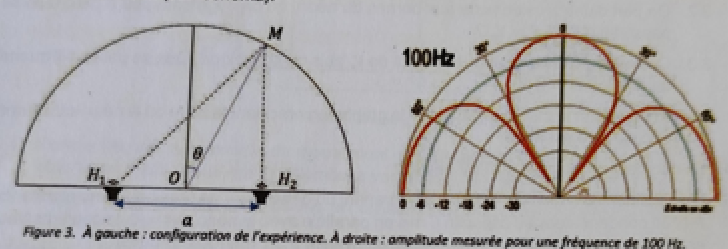
4.1. Calculer H1M et H2M. ( H2M est orthogonal à H1H2).
H2M = OM cos 30 = 3 xcos 30 =2,6 m.
H1M2 = a2 +MH22 =32+2,62=15,76 ; H1M =3,97 ~ 4,0 m.
4.2 Calculer le temps t1 mis par le signal émis par H1 pour arriver en M.Calculer le temps t2 mis par le signal émis par H2 pour arriver en M.
t1 =4 /340= 0,0117 s ~11,7 ms.
t2 =2,6 /340= 0,0076 s ~7,6 ms.
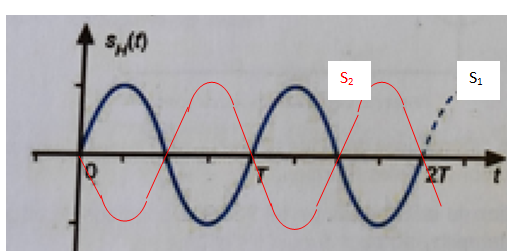
4.3 Dessiner le signal sM1(t) reçu en M depuis H1 et le signal sM2(t) reçu en M depuis H2.
T = 1 / f = 1 /100 = 0,010 s = 10 ms.
11,7-7,6 = 4,1 ms.
Les deux signaux reçus en M sont pratiquement en opposition de phase.
La somme de ces deux signaux est proche de zéro. Le son perçu en M est
donc très faible.
D. Spectacle électrostatique.
On installe une boule conductrice de centre O de rayon R = 0,10 m que
l'on charge en surface. La boule est suspendue en l'air à une distance
d =1 m du sol.
1. On note s > 0 la charge surfacique. Quelle est la relation entre s et la charge totale Q de la boule ?
Q = s x surface de la boule = s x 4 p r2.
2. Expliquer pourquoi le champ électrique créé par la boule en un point M est radial.
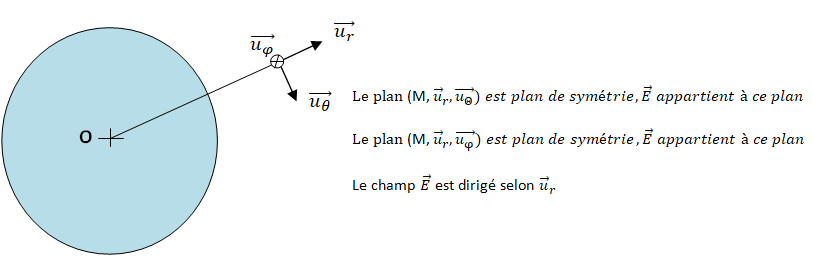
3. Citer le
théorème de Gauss et l'appliquer à une surface de Gauss à préciser
poour montrer créé par la boule en un point M extérieur a l'expression
suivante.
Le
flux du champ électrique à travers une surface S fermée est égal à la
somme des charges contenues dans le volume V délimité par cette surface
divisée par e0.
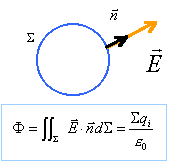
On considère une sphère
S , de centre O et de
rayon r.
Soit un point M situé à une distance x >
R : F = E
4px²
D'autre part la charge contenue à
l'intérieure de S
est la charge totale de la sphère de rayon R : Q =
s
4pR².
d'où E = s
R² / (e0x²).
4. Quelle relation lie le champ au potentiel V(r). Calculer l'expression de v(r) en supposant le potentiel nul à l'infini.
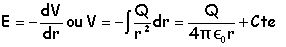
La constante d'intégration est nulle, le potentiel électrique étant nul à l'infini.
Pour faire apparaître un arc électrique, il faut dépasser la tension de
claquage dans l'air de l'ordre de Vc=3600 kV par mètre d'air traversé.
Quelle doit être la charge Q de la boule pour faire apparaître un
éclair entre sa surface et le sol ( de potentiel nul )?
Combien d'électrons doit-on arracher à sa surface pour obtenir cette
charge ?
e0 = 8,85 10-12 F m-1 ; e = 1,6 10-19 C.
Vc = Q / (4 p e0 d) ;
Q =Vc 4 p e0 d =3,6 106 x4 x3,14 x8,85 10-12 =4,0 10-4 C.
Nombre d'électrons : 4,0 10-4 / (1,6 10-19) =2,5 1015.
E. Lancer de tomates.
Masse d'une tomate m = 200 g. On néglige les frottements de l'air. A
l'instant t=0, la tomate est au point O, animée d'une vitesse v0 = 10 m /s.
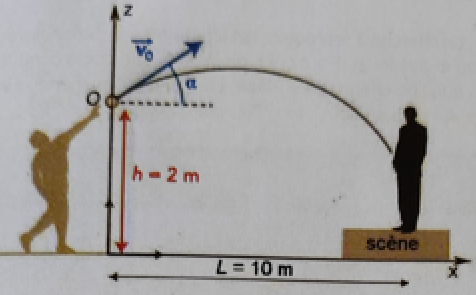
1. Donner les expressions des accélérations verticale et horizontale.
La tomate n'étant soumise qu'à son poids, la seconde loi de newton conduit à :
az = -g et ax = 0.
2. Donner les expressions de x(t) et z(t).
La vitesse est une primitive de l'accélération : vx = v0 cos a ; vz = -gt +v0 sin a.
La position est une primitive de la vitesse :
x=v0 cos a t.
z = -½gt2 +v0 sin at .
3. Donner l'expression de la trajectoire.
t = x /(v0 cos a).
Repport dans z : z = -½gx2 /(v0 cos a)2 + x tan a .
4. Montrer que la tomate frôle la tête du chanteur ( x = L et z = 0) à la condition suivante sur l'angle de départ sin (2a) = gL / v02.
On donne sin a cos a = sin(2a) / 2.
0= -½gL2 /(v0 cos a)2 + L tan a
0= -½gL /(v02 cos a) + sin a
½gL = v02 cos a sin a.
gL /v02 = 2cos a sin a= sin(2a).
5. Calculer a.
sin(2a) =9,81 x10 / 100 =0,981 ; 2a~79° ; a ~39°.
6.
Calculer le temps que met la tomate pour rriver sur son objectif.
Le temps de réaction d'un humain est d'une seconde. Le chanteur
réussit-il à échapper à la tomate ?
L=v0 cos a t.
t =10 /(10 x cos39)=1,3 s.
Il peut échapper à la tomate.
|
ane.
|
|
|