Mathématiques.
Concours contrôleur des douanes 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1.
En
2020,M. DUFISC a fait sa première déclaration de revenus : il a déclaré
un revenu annuel de 90 000 €, l’impôt correspondant s’est élevé à 8 000
€ et son revenu après impôt a donc été de 82 000 €. Chacune des quatre
années suivantes, son revenu annuel a augmenté de 2 % et l’impôt
correspondant a augmenté de 3 %.
M. DUFISC souhaite étudier ce qu’il adviendrait de son revenu après paiement de l’impôt si l’évolution constatée se poursuivait.
Dans ce but, on suppose que l’évolution constatée se poursuit et, pour tout entier n positif ou nul, on note :
• Rn lemontant exprimé en euros du revenu annuel de M. DUFISC en l’an (2020+n) ;
• In lemontant exprimé en euros de l’impôt correspondant ;
• Un = Rn −In.
Ainsi R0 = 90000; I0 = 8000;U0 = 82000.
1. a. Calculer R1 ; I1 ;U1 ; R2 ; I2 ;U2.
R1 = R0 x1,02 =90 000 x1,02=91 800.
I1 =I0 x1,03 =8000 x1,03=8240.
U1 =91 800 -8 240=83 560.
R2 = R1 x1,02 =91 800 x1,02=93 636.
I2 =I1 x1,03 =8240 x1,03=8487,2.
U2 =93 636 -8 487,2=85 148,8.
b. Montrer que, pour tout entier n positif on a :
Rn =90000×(1,02)n et In = 8000×(1,03)n.
Rn est une suite géométrique de premier terme 90 000 et de raison 1,02.
Rn =90 000×(1,02)n .
In est une suite géométrique de premier terme 8 000 et de raison 1,03.
In =8 000×(1,03)n .
2. a. Montrer que pour tout entier n positif,Un+1−Un = 1800×(1,02)n −240×(1,03)n .
Un+1= Rn+1 -In+1 ; Un= Rn -In ; Un+1−Un =Rn+1 -Rn -(In+1 -In ).
Rn+1 -Rn =90 000×(1,02)n+1 -90 000×(1,02)n =1,02n (90 000 x1,02 -90 000)=1800×(1,02)n .
In+1 -In =8 000×(1,03)n+1 -8 000×(1,03)n =1,03n (8000 x1,03-8000)=240×(1,03)n .
b. Montrer que : Un+1 < Un équivaut à : n ×ln(1,03 /1,02 ) > ln(15 /2).
Un+1 < Un équivaut à Un+1 - Un < 0.
1800×(1,02)n −240×(1,03)n < 0 ;
7,5 ×(1,02)n −(1,03)n < 0 ;
7,5 ×(1,02)n <(1,03)n .
ln(7,5) +n ln(1,02) < n ln(1,03).
ln(7,5) < n ln(1,03) -n ln(1,02).
ln(7,5 )< n ln(1,03 / 1,02)
On admettra que les entiers n supérieurs ou égaux à 207 vérifient n ×ln(1,03 / 1,02 )> ln(7,5).
3. Si l’évolution
que M.DUFISC a constatée concernant son revenu et l’impôt correspondant
se poursuit, voit-il son revenu après l’impôt diminuer ?
Le revenu diminue : Un+1 < Un équivaut à : n ×ln(1,03 /1,02 ) > ln(15 /2).
Le revenu diminue si n > 207 ; année 2020 +207 =année 2227.
Il ne vera pas son revenu diminuer.
Exercice 2
Depuis
une décennie, le nombre de candidats admis au baccalauréat augmente
régulièrement à Clermont-Ferrand. Les responsables du campus
universitaire décident de mener une étude sur les besoins en
infrastructures et équipements du campus puis une enquête auprès d’un
échantillon d’étudiants sur leur préférence entre le renforcement du
parc automobile
et la construction de nouvelles résidences universitaires.
L’étude menée sur la période allant de 2015 à 2020 a permis de
modéliser l’évolution du nombre de nouveaux étudiants demandeurs de
logements dans les résidences universitaires par la suite (un) définie pour tout entier naturel n par :
un = 1000·[0,5 n+1-ln(0,5 n+1)].
(un) étant le nombre d’étudiants en (2015+n).
Arthur, le premier responsable des étudiants, a pris connaissance des
résultats de l’étude menée. Afin de connaître l’évolution du nombre
d’étudiants demandeurs de logements dans les résidences universitaires,
il se propose d’étudier les variations de la fonction f définie sur [0
; +oo [ par :
f (x) =0,5 x+1-ln(0,5x+1).
Il se propose également d’analyser les résultats issus de l’enquête.
Partie A
1. Déterminer le nombre de nouveaux étudiants demandeurs de logements dans les résidences en 2015 puis en 2020.
En 2015, n =0 : u0=1000 [0+1-ln(1)] =1000.
En 2020, n = 5 : u5=1000[2,5+1-ln(3,5)]~2 247.
2. a. Calculer la dérivée de f (x) pour tout x appartenant à [0 ; +oo [.
f ' (x)=0,5-0,5 /(0,5x+1)=0,5 (1-1/(0,5x+1))=0,5 x0,5 x / (0,5x+1)=0,25x / (0,5x+1).
b. Étudier le sens de variation de f (x).
f '(x) > 0 sur [0 ; +oo [ ; f(x) est strictement croissante.
3. Dresser le tableau de variations de la fonction f (x) sur l’intervalle [0 ; +oo [.
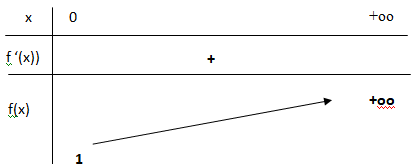
4. Justifier que la suite (un) est croissante.
un =1000 f(n). La fonction f étant strictement croissante, il en est de même de un.
Partie B
Un groupe de 100 étudiants composé de 60 garçons et 40 filles a
participé à l’enquête sur la préférence entre le renforcement du parc
automobile et la construction des résidences universitaires. 40 % des
garçons sont favorables au renforcement du parc et 60 % des filles
optent pour la construction des résidences universitaires.
1. Déterminer :
a. le nombre de garçons ayant opté pour la construction de nouvelles résidences.
60 (1-0,4) =36.
b. le nombre total d’étudiants ayant opté pour la construction des nouvelles résidences.
36 +40 x0,6=60.
2. On interroge un étudiant au hasard.
Déterminer la probabilité des événements suivants :
a. A : l’étudiant préfère la construction de nouvelles résidences.
p(A) = 0,6.
b. B : l’étudiant est une fille qui a opté pour le renforcement du parc automobile.
p(B) =0,4x40 / 100 =0,16.
|
...
|
....
|
Exercice 3.
On considère la fonction f définie sur ]0 ; +∞[ par f (x) = x2−8ln(x).
On admet que f est dérivable sur son ensemble de définition et on note f ′ sa fonction dérivée.
1. Déterminer les limites de la fonction f aux bornes de son ensemble de définition.
Quand x tend vers zéro, ln(x) tend vers -oo et x2 tend vers zéro.
-8 ln(x) tend vers +oo ; f(x) tend vers +oo.
Quand x tend vers +oo : f(x) = x2(1-8ln(x) / x2).
Par croissance comparée ln(x) / x2 tend vers zéro ; f(x) tend vers +oo.
2. Calculer la dérivée de la fonction f .
f '(x) = 2x-8 / x =2(x2-4) / x.
3. Étudier les variations de f sur ]0 ; +∞[ et dresser son tableau de variation complet. On précisera la valeur exacte du minimum.
x étant positif, f '(x) a le signe de x2-4.
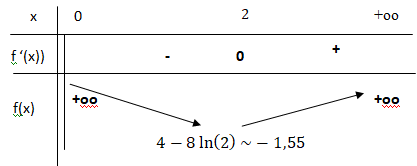
4. Démontrer que sur l’intervalle ]0 ; 2], l’équation f (x) = 0 admet une solution unique a.
La fonction f est continue car dérivable et strictement décroissante sur l(intervalle ]0 ; 2].
De plus f(0) tend vers +oo et f(2) ~-1,55.
D'après le théotème de la bijection, l'équation f(x) = 0 admet une unique solution sur l’intervalle ]0 ; 2]
5. On admet que sur l’intervalle ]2 ; +∞[, l’équation f (x) = 0 admet une solution unique ß.
En déduire le signe de f sur l’intervalle ]0 ; +∞[.
Sur ]a ; ß[, f(x) < 0.
Sur ]0 ; a[ union ]ß ; +oo[ f(x) est positive.
6. Pour tout réel k, on considère la fonction gk définie sur]0 ; +∞[ par :
gk (x)= x2 −8ln(x)+k.
En s’aidant du tableau de variation de f , déterminer la plus petite valeur de k pour laquelle la fonction gk est positive sur l’intervalle ]0 ; +∞[.
gk(x) = f(x) +k.
gk(x) > 0 si k > 4-8 ln(2).
Exercice 4.
On dispose d’une urne contenant 6 jetons indiscernables au toucher dont :
• trois jetons numérotés 1;
• deux jetons numérotés 2;
• un jeton numéroté 3.
et d’un dé cubique bien équilibré dont les faces sont numérotées 1, 1, 2, 2, 2, 3.
L’épreuve (E) consiste à tirer au hasard et simultanément deux jetons de l’urne et à lancer une fois le dé.
On effectue une épreuve. On suppose que tous les événements élémentaires sont équiprobables.
Arbre pondéré représentant le dé :
Le nombre 1 étant présent 2 fois, sa probabilité d'apparition est 2 / 6 = 1 / 3.
Le nombre 2 étant présent 3 fois, sa probabilité d'apparition est 3 / 6 = 1 / 2.
Le nombre 3 étant présent 1 fois, sa probabilité d'apparition est 1 / 6.
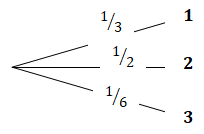
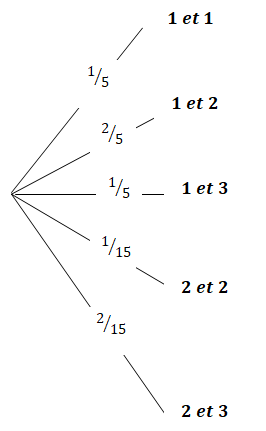
Arbre pondéré représentant le dé :
Tirer deux nombres 1 : (2 3) / (2 6)=3 / 15= 1 /5
Tirer le nombre 1 et le nombre 2 : (1 3) x (1 2)/ (2 6)=6 / 15 = 2 / 5
Tirer le nombre 1 et le nombre 3 : (1 3) x (1 1)/ (2 6)=3 / 15 = 1 / 5.
Tirer deux nombres 2 : (2 2) / (2 6)=1 / 15.
Tirer le nombre 2 et le nombre 3 : (1 2) x (1 1)/ (2 6)=2 / 15.
1. Calculer les probabilités des événements suivants :
A : « le produit des trois numéros obtenus est égal à 4 »;
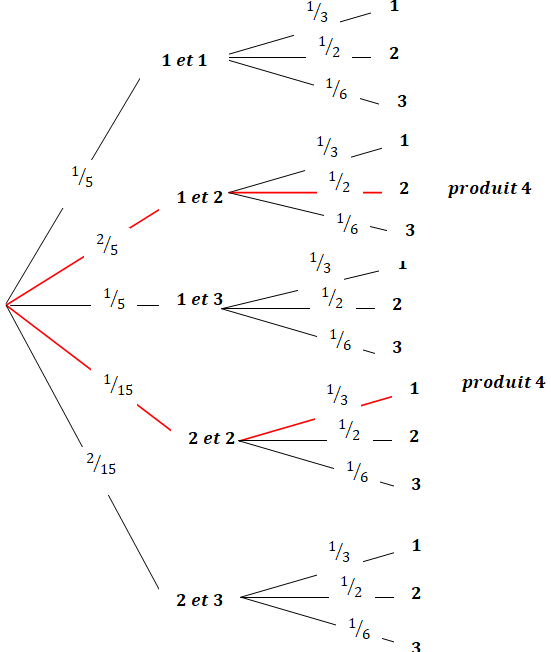
2 /5 x 1 /2 +1 /15 x 1 /3 = 1 /5 +1 /45 =10 /45 =2 /9.
• B : « la somme des trois numéros obtenus est égale à 5 ».
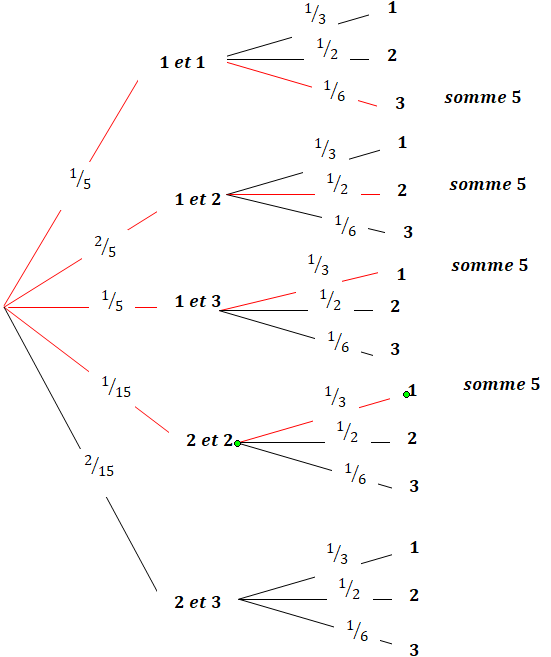
1 /5 x 1 /6 + 2 / 5 x1 /2 +1 / 5 x 1 / 3+1/15 x1 / 3 =1 /30 +1 /5 +1 /15 +1 /45=(3+18+6+2)/90=29 / 90.
2. Soit X la variable aléatoire égale au nombre de numéro 2 lors d’une épreuve.
Donner la loi de probabilité de X et en dresser le tableau.
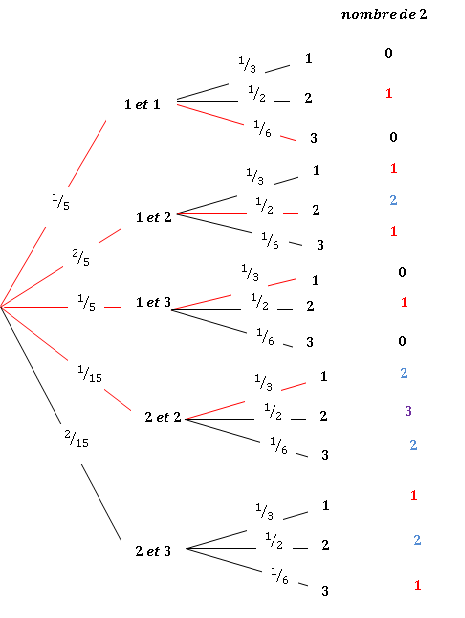
p(X=0) =2/15 +1 /30 +1/15+1/30=6 /30=1/5.
p(X=1) =1/10 +2/15 +1/15+1/10+1/45+2/45=(9+12+6+9+2+4)/90=42 /90= 7 /15.
p(X=2)=2 / 5 x1 /2 +1/15 x1/3+1/15 x1/6+2/15 x1/2=1/5+1/90+1/15=(18+2+1+6)/90=27/90=3/10.
p(X=3) = 1 /15 x1/2)1/30.
xi
|
0
|
1
|
2
|
3
|
p(X=xi)
|
1 / 5
|
7 /15
|
3/10
|
1/30
|
3. Lors d’une épreuve, on appelle « succès » l’obtention de trois numéros impairs.
Montrer que la probabilité d’avoir un succès est égale à 1 /5.
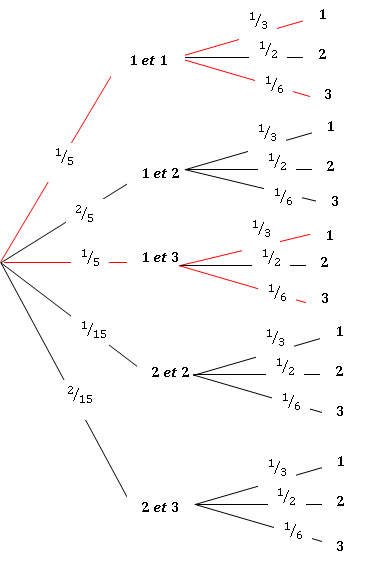
1 / 5 x 1 / 3 +1 /5 x 1 / 6 +1 /5 x 1 /3 +1 /5 x1 /6=1/15+1/30+1/15+1/30=(2+1+2+1)/30=6 /30 = 1 /5.
4. Soit n entier naturel > 1. On répète n fois de suite et d’une manière indépendante l’épreuve (E). Calculer la probabilité Pn de l’événement An : « obtenir au moins un succès lors des n épreuves ».
Chaque épreuve E posséde deux issues ; L'épreuve est répétée n fois de
manière indépandante. La variable aléatoire Y donnant le nombre de
succès sur n épreuves suit la loi binomiale de paramètres n et p = 1 /5.
Pn = P(An) = P(Y > 1 ) = 1-P(Y=0)=1-(0 n) (1/5)0(1-1/5)n-0=1-(4/5)n.
|
|