Mathématiques,
bts groupe D 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
. |
..
..
......
...
|
EXERCICE 1 10 points
Les questions 1. à 5. de cet exercice peuvent être traitées
indépendamment les unes des autres. Les probabilités seront arrondies à
10−3.
De par la diversité des coccinelles, on peut utiliser deux critères pour reconnaître certaines espèces de coccinelles :
— la taille de la coccinelle
— le type de pronotum (le pronotum est la face dorsale d’une partie du thorax de la coccinelle.
Un type de pronotum répandu est le pronotum dit de type P.
1. On s’intéresse à toutes les coccinelles présentes dans une forêt d’Europe.
Des études statistiques montrent que :
• 25% des coccinelles présentes dans cette forêt ont une taille
inférieure ou égale à 5 mm; parmi les coccinelles qui ont une taille
inférieure ou égale à 5mm, 40% ont un pronotum de type P;
• Parmi les coccinelles présentes dans cette forêt de taille strictement supérieure à 5mm, 68% ont un pronotum de type P.
Dans cette forêt, on prélève au hasard une coccinelle. On appelle :
• T l’évènement : « la coccinelle a une taille inférieure ou égale à 5 mm»;
• P l’évènement ;« la coccinelle a un pronotum de type P ».
a. Compléter l’arbre modélisant la situation décrite ci-dessus.
Pour les questions b. à d., on prélève au hasard une coccinelle dans la forêt.
b. Déterminer la
probabilité de l’évènement A : « la coccinelle prélevée a une taille
inférieure ou égale à 5 mm et n’a pas un pronotum de type P ».
c. Déterminer la probabilité de l’évènement B : « la coccinelle prélevée dans la forêt n’a pas un pronotum de type P ».
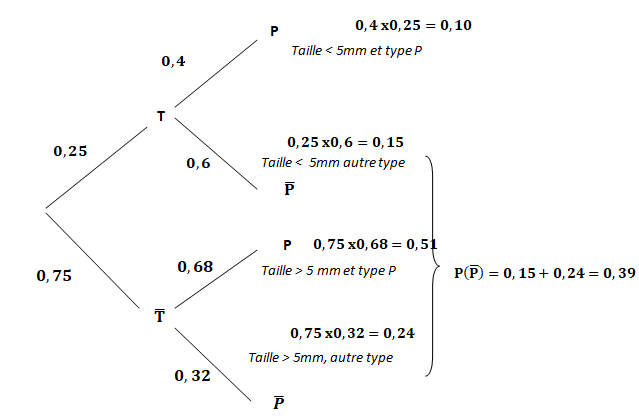
d. Déterminer la
probabilité que la coccinelle prélevée soit de taille inférieure ou
égale à 5 mm sachant qu’elle n’a pas un pronotumde type P.
P non P (T) =P(non P n T) / P(non P) =0,15 /0,39 =0,385.
2.
Les critères « avoir une taille moyenne inférieure ou égale à 5 mm» et
« ne pas avoir un pronotum de type P » caractérisent une espèce
particulière : la coccinelle à deux points.
On appelle X la variable aléatoire qui, à tout échantillon de 10
coccinelles prélevées au hasard dans cette forêt, associe le nombre de
coccinelles à deux points dans l’échantillon.
La population de coccinelles de la forêt est suffisamment importante
pour que ce prélèvement soit assimilé à un tirage avec remise. On admet
que la probabilité de prélever au hasard dans la forêt étudiée une
coccinelle à deux points est égale à 0,15.
a. Donner la loi suivie par la variable aléatoire X et préciser ses paramètres. On ne justifiera pas la réponse.
Loi binomiale de paramètre n =10 et p = 0,15.
b.
On prélève au hasard 10 coccinelles dans la forêt étudiée. Calculer la
probabilité d’avoir au moins une coccinelle à deux points dans le
prélèvement.
P(X > 1) = 1-P(X =0)=1-0,197=0,803.
3.
On considère un élevage de coccinelles. On note L la variable aléatoire
qui, à chaque coccinelle de l’élevage associe sa taille. On estime que
cette taille exprimée en mm suit la loi uniforme sur l’intervalle [3;
6].
a. On prélève au
hasard une coccinelle dans cet élevage. Quelle est la probabilité que
sa taille soit comprise entre 4 mm et 5 mm ?
(5-4) / (6-3) =1 /3.
b. Quelle est la taille moyenne des coccinelles dans cet élevage ?
(3+6) / 2 = 4,5 mm.
4. On s’intéresse ici à la ponte d’une espèce
particulière de coccinelles : les coccinelles à deux points. On
modélise le nombre d’oeufs par ponte à l’aide d’une variable aléatoire
U qui suit la loi normale d’espérance égale à 35 et d’écart-type égal à
6.
a. Donner le nombre moyen d’oeufs par ponte d’une coccinelle à deux points.
35 oeufs.
b. Calculer la probabilité p(31< U < 39).
P(U < 31)=0,252 ; P(U < 39)=0,7475 ; p(31< U < 39) =0,7475 -0,252 =0,495.
c. Déterminer un nombre entier h tel que : p(35−h <U <35+h) ≈0,95 à 10−2 près.
Interpréter sous forme d’une phrase la probabilité correspondante dans le contexte.
1,96 s=1,96 x6 =11,76 ~12.
Intervalle de confiance : [35-12 ; 35 +12) soit [23 ; 47].
95 coccinnelles de cette espèce sur 100 pondent entre 23 et 47 oeufs.
5. Une autre espèce spécifique est utilisée dans la lutte contre l’infestation des pucerons.
Michel a créé un mur végétalisé. Avec effroi, il constate une infestation de pucerons.
Sachant
que les larves de cette espèce spécifique de coccinelles dévorent un
grand nombre de pucerons, il en commande un lot de 80 larves pour
traiter le mur. Le vendeur annonce que la durée de vie de ces larves,
en jours, suit la loi normale d’espérance m = 20 et d’écart-type s = 3.
Michel constate que la durée de vie moyenne des larves de son lot n’est que de 18 jours.
Peut-il remettre en question l’annonce du vendeur au seuil de confiance de 95% ?
1,96 x3 / 80½ =0,657.
Intervalle de confiance : 20-0,657 ; 20 +0,657) soit [19,3 ; 20,7]. L'annonce du vendeur n'est pas correcte.
|
...
|
....
|
EXERCICE 2 10 points
Cet exercice est composé de trois parties indépendantes entre elles
Dans une usine agroalimentaire. il y a une seule ligne de production
qui fonctionne en continu. Elle peut fabriquer deux variétés M1 et M2
d’un même produit, qui diffèrent par leur teneur en matière grasse :
— la variété M1 correspond à une teneur idéale en matière grasse de 8,6%, soit 0,086;
— la variété M2 correspond à une teneur idéale en matière grasse de 15,2%,soit 0,152.
La ligne était réglée jusqu’alors pour produire la variété M1. On
injecte continûment de la matière grasse dans le produit en
fabrication, sans arrêter la ligne de production, jusqu’à obtenir la
variété M2. Durant cette phase de transition, la production est
recyclée.
La variété M2 est considérée commercialisable par le service qualité
dès que sa teneur en matière grasse dépasse 14,9%, soit 0,149.
Partie A
La phase de transition pour passer de la variété M1 à la variété M2 est
lancée. Un prélèvement est réalisé toutes les minutes pour mesurer la
teneur en matière grasse du produit (le temps t =0 correspond au
démarrage de la période de transition).
Les résultats sont rassemblés dans le tableau ci-dessous :
t(min)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
teneur en matière grasse y
|
0,086
|
0,108
|
0,121
|
0,131
|
0,14
|
0,144
|
0,147
|
0,149
|
0,149
|
0,151
|
0,151
|
z = ln(0,152-y)
|
-2,72
|
-3,12
|
-3,47
|
-3,86
|
-4,42
|
-4,83
|
-5,30
|
-5,81
|
-5,81
|
-6,91
|
-6,91
|
1. Le nuage de points est représenté sur le graphique ci-dessous.
Un ajustement linéaire paraît-il approprié ? Pourquoi ?
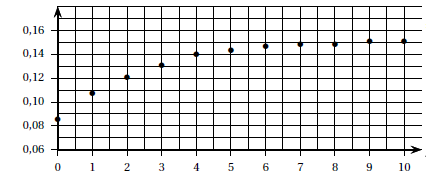
Non, les points ne sont pas alignés.
a. Indiquer sur la copie les deux valeurs manquantes z1 et z2 du tableau.
b. À l’aide
de la calculatrice, déterminer par la méthode des moindres carrés une
équation de la droite d’ajustement du nuage de points (t ; z ) sous la
forme z = at +b.
z = -0,442 t-2,635.
c. Pour cette question, on prendra a = −0,44 et b = −2,7.
Déterminer une expression de la fonction y ajustant le nuage de points (t ; y) dans le cadre de cette modélisation.
-0,44 t-2,7 = ln(0,152-y).
exp(-0,44t -2,7) = 0,152-y.
y = 0,152 -exp(-0,44t -2,7).
y=0,152-0,067 exp(-0,44t).
Partie B
1. L’étude expérimentale menée conduit à considérer la fonction C définie sur [0; 10] par :
C(t )= 0,152−0,067exp(−0,44t).
On admet que la fonction C modélise la teneur en matière grasse du
produit (nombre entre 0 et 1) en fonction du temps en minutes, décompté
depuis le démarrage de la période de transition.
a. Calculer l’arrondi de C(2) à 10−3. Interpréter par rapport à la situation étudiée.
C(2) =0,152-0,067 exp(-0,88)=0,124.
Au bout de 2 min, la teneur en matière grasse est 0,124.
b. Calculer la dérivée de la fonction C et en déduire le sens de
variation de la fonction C sur [0; 10]. Ce résultat est-il cohérent
avec la situation étudiée ?
C'(t) =0,067 x0,44 exp(-0,44 t) >0.
La fonction C(t) est strictement croissante.
2. On considère l’algorithme suivant rédigé en langage naturel.
Quelle est la valeur numérique renvoyée par cet algorithme lorsqu’il a été exècuté ?
M prend la valeur 0
D prend la valeur 0,085
Tant que D < 0,149
M prend la valeur M+1
D prend la valeur C(M)
Fin Tant que
Renvoyer M.
Cet algorithme renvoie la durée en minute au bout de laquelle la teneur en matière grasse atteint la valeur 0,149.
3. a. On
admet que l’équation C(t ) = 0,149 admet une unique solution, notée T ,
sur l’intervalle [0; 10]. Déterminer une valeur approchée de T à 10−2 près.
0,152−0,067exp(−0,44t)= 0,149 ; exp(-0,44t) = 0,04478 ;
-0,44 t = ln(0,04478) ; t =7,06 min.
b.
Déduire de la question précédente le temps, à la seconde près, qu’il
faut attendre après le démarrage afin d’obtenir une variété M2
commercialisable..
7 min 4 s.
Partie C
On considère la fonction f définie sur l’intervalle [0; 10] par f (t ) =0,152−0,062exp(−0,5t ).
Le génie des procédés permet de considérer que la fonction constitue
une autre modélisation acceptable de la teneur en matière grasse du
produit en fonction du temps t en minutes qui s’est écoulé à partir du
démarrage de la période de transition.
On admet que le plus grand nombre réel t appartenant à l’intervalle [0; 10] tel que f (t ) < 0,149 vaut approximativement 6 au dixième près.
1. On considère la fonction F définie sur l’intervalle [0; 10] par
FCt )= 0,152t +0,124exp(−0,5t) .
Vérifier que la fonction F est une primitive de la fonction f sur l’intervalle [0; 10].
Calcul de la dérivée FCt ' =0,152 -0,124 x0,5 exp(-0,5t) = 0,152 -0,062 exp(-0,5 t) = f(t).
2. a. Déduire de la question précédente que l’arrondi à 10−4 de 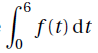 est 0,794 2. est 0,794 2.
F(6)-F(0) = 0,152 x 6+0,124 exp(-3)-0,124=0,7942.
b. Hachurer sur le graphique fourni le domaine dont l’aire est égale à la valeur de cette intégrale.
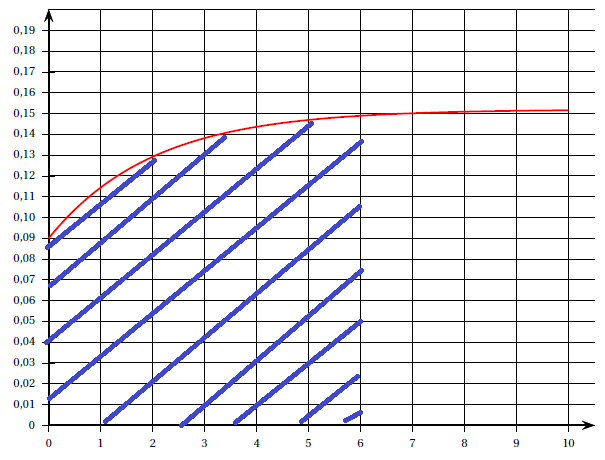
c. On note 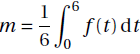
.Calculer l’arrondi du réel m à 10−3 et interpréter la valeur obtenue dans le contexte de l’exercice.
m=0,794 / 6=0,132.
Au bout de 6 min, la teneur moyenne en matière grasse est de 0,132.
|
|
|
|
|