Mathématiques, bts groupe C 2024

Le bois d’épicéa est couramment utilisé en France pour la construction.
Avant son utilisation, il est nécessaire de le faire sécher.
La teneur en humidité du bois d’épicéa correspond au pourcentage d’eau contenu dans le bois.
On considère ici des poutres d’épicéa ayant la forme d’un pavé droit de longueur 4 m et dont la base est un carré de côté 5 cm.
Etude statistique.
On a effectué un relevé de la teneur en humidité d’une poutre en épicéa en fonction du temps, exprimé en semaine. Les données sont représentées sur le graphique ci- dessous.

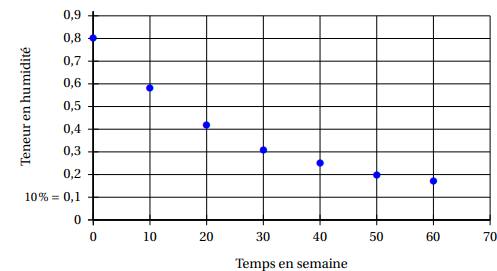1. Au vu de la représentation graphique obtenue, un ajustement affine semble-t-il approprié ? Expliquer.
Un ajustement affine n'est pas approprié, les points n'étant pas alignés.
2. On désigne par H la teneur en humidité dans le bois, en pourcentage, et on pose : y = ln(H −0,1).

t	0	10	20	30	40	50	60
H	0,80	0,58	0,42	0,32	0,25	0,20	0,17
y	-0,36	-0,73	-1,14	-1,51	-1,90	-2,30	-2,66

a. Dans le tableau, quelle est la valeur manquante y, arrondie au centième, correspondant au temps t = 30 ?
b. Sans justifier, donner une équation de la droite d’ajustement de y en t, par la méthode des moindres carrés. Arrondir les coefficients au millième.
y =-0,039 t -0,356.
c. Déduire de la question précédente un ajustement de H par t.
H-0,1= exp(y) ; H = exp(y) +0,1 = exp(-0,039t-0,356) +0,1.
On admet dans la suite que l’évolution de la teneur en humidité de la poutre, en fonction du temps, est donnée par l’expression H(t) = 0,7exp(−0,04t) +0,1.
d. Quelle serait la teneur en humidité de la poutre après 70 semaines ? Arrondir le résultat au millième.
H(70) =0,7 exp(-0,04 x70)+0,1 =0,14 ( 14 %).
e. Est-il possible que la teneur en humidité soit inférieure à 5% ?
0,7exp(−0,04t) +0,1 <0,05 ; exp(−0,04t) < (0,05-0,1) / 0,7.
Impossible, le terme en exponentielle étant toujours positif.

Partie A -modélisation de la teneur en humidité.
Dans cette partie, on utilisera exclusivement des valeurs exactes pour les calculs.
1. On considère que lors du séchage 96% de la surface extérieure d’une poutre est exposée à l’air.
Montrer que pour de telles poutres, la valeur correspondante à l’aire de la surface exposée à l’air vaut 0,772 8 m².
Aire latérale :4 x0,05 x4 =0,8 m² ; aire des deux extrémités : 2 x0,05² =0,005 m².
Aire totale : 0,805 m² ; 0,805 x0,96=0,772 8 m².
2. On admet que pour le bois considéré dans cette partie et les conditions de séchage envisagées, la teneur en humidité, exprimée en pourcentage, est une fonction f du temps t exprimé en semaine, qui vérifie l’équation différentielle :
(E) : y′+0,03864y =0,003864
où y est une fonction dérivable sur l’intervalle [0 ; +∞[ et y′ est sa fonction dérivée.
a. Vérifier que la fonction g définie sur [0 ; +∞[ par g(t ) = 0,1 est une solution particulière de l’équation (E).
g'(t) =0 ; repport dans (E) : 0 +0,03864 x 0,1 = 0,003864.
b. Déterminer les solutions de l’équation homogène (E₀) :
(E₀) : y′ +0,03864y = 0.
y = A exp(-0,03864 t) avec A une constante.
c. Déduire de ce qui précède, les solutions de l’équation différentielle (E).
y = A exp(-0,03864t) +0,1.
d. Déterminer la fonction f , définie sur [0 ; +∞[, solution de l’équation différentielle (E) telle que la teneur en humidité initiale, c’est-à-dire au temps t = 0, est de 80%.
0,80 = A+0,1 ; A = 0,70.
y = 0,70 exp(-0,03864t) +0,1.

Partie B - Temps de séchage
On admet que la fonction représentée ci-dessous est la fonction f qui exprime la teneur en humidité du bois d’épicéa, en pourcentage, en fonction du temps t , exprimé en semaine.

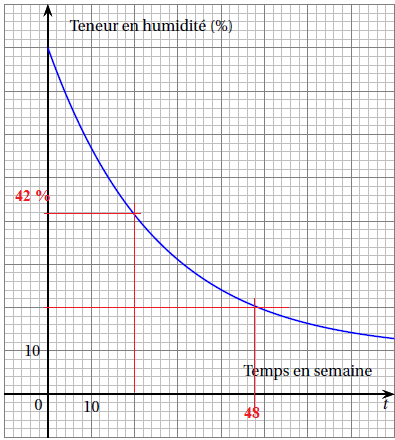
1. Quelle est la teneur en humidité d’une poutre après 20 semaines de séchage?
2. Ces poutres sont vendues une fois que leur teneur en humidité est inférieure à 20 %.
Au bout de combien de temps, ces poutres peuvent elles être vendues ?

Partie C - Teneur en humidité
Dans cette partie, on admet que l’expression de la fonction f définie sur [0 ; +∞[ représentant la teneur en humidité, en pourcentage, du bois d’épicéa en fonction du temps t , exprimé en semaine, est :
f (t )= 0,7exp(−0,04t) +0,1.
1. En utilisant les résultats précédents, répondre aux questions suivantes :
a. Donner la limite de f lorsque t tend vers +∞.
Interpréter ce résultat dans le contexte de l’exercice.
Le terme en exponentielle tend vers zéro ; f(t) tend vers 0,1.
Au bout d'un temps suffisamment long, la teneur en humidité tend vers 10 %.
b. À l’aide du contexte, conjecturer les variations de la fonction f sur [0 ; +∞[.
f(t) est décroissante.
c. Étudier les variations de la fonction f sur l’intervalle [0 ; +∞[.
f '(t) = -0,7 x0,04 exp(-0,04t) < 0 ; f(t) est strictement décroissante de 0,71 à 0,01.
2. a. Résoudre pour t appartenant à [0 ; +∞[ l’inéquation : f (t ) < 0,2.
Arrondir le résultat à l’unité.
0,7exp(−0,04t) +0,1 < 0,2.
exp(-0,04t) < 0,143.
-0,04t < ln(0,143) ; t > 48,6 ; t > 49.
b. Interpréter le résultat dans le contexte de l’exercice.
Au bout de 49 semaines, l'humidité est inférieure à 20 %.

Exercice 2
Les différentes parties de cet exercice sont indépendantes.
Une entreprise produit en grande série des vis au moyen de deux chaînes de production.
Partie A - Production de vis
On choisit au hasard une vis dans le stock. On note :
• C1 l’évènement « la vis provient de la première chaîne »;
• C2 l’évènement « la vis provient de la deuxième chaîne »;
• D l’évènement « la vis a un défaut ».
La première chaîne produit 40% du stock et on sait que sur cette chaîne 3 vis sur 1 000 ont un défaut.
De plus, on sait que sur la deuxième chaîne, 5 vis sur 1 000 ont un défaut.
1. Recopier et compléter l’arbre pondéré suivant :

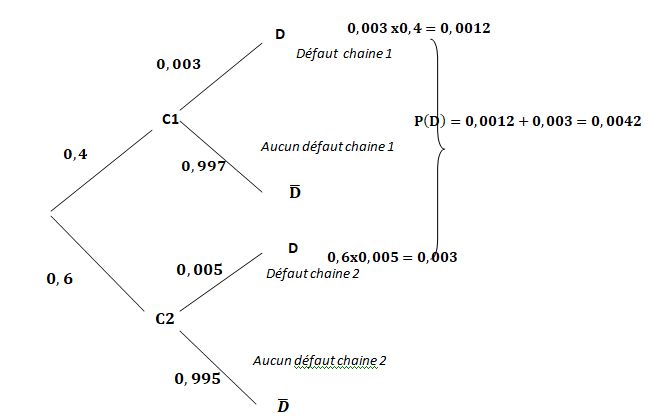
2. Déterminer la probabilité que la vis choisie provienne de la première chaîne et présente
un défaut.
3. Montrer que la probabilité que la vis présente un défaut est égale à 0,0042.
4. On choisit une vis du stock et on constate qu’elle présente un défaut.
Est-il exact qu’il y a moins de 25 % de chances qu’elle provienne de la première chaîne de production ?
P_D C1 =P(D n C1) / P(D) =0,0012 / 0,0042=0,286 (28,6 %). Affirmation fausse.

Partie B - Étude d’un lot
Dans cette partie, on admet que la probabilité qu’une vis ait un défaut vaut 0,004.
On prélève, dans le stock d’une journée, un lot de 50 vis. On admet que ce stock est suffisamment important pour que ce prélèvement soit assimilé à un tirage avec remise.
On note X la variable aléatoire qui à chaque prélèvement d’un lot de 50 vis, associe le nombre de vis ayant un défaut.
1. Expliquer pourquoi la variable aléatoire X suit une loi binomiale dont on précisera les paramètres.
Répétition d' épreuves identiques et indépendantes.
L'expérience peut être assimilée à un tirage aléatoire avec remise. ( schéma de Bernoulli).
X suit la loi binomiale de paramètre n = 50 et p =0,04.
2. Dans cette question, les probabilités seront arrondies au millième.
a. Calculer la probabilité que ce lot contienne exactement 2 vis ayant un défaut.
P(X=2) =0,016.
b. Calculer la probabilité que ce lot contienne au moins 3 vis ayant un défaut.
P(X >3 )= 1-P(X <2) =1-0,9989 =0,00109 ~0,001.

Partie C - Conformité des vis
Dans cette partie, on s’intéresse à la longueur des vis produites par la première chaîne de production.
On appelle L la variable aléatoire qui, à chaque vis de la production, associe sa longueur en millimètre.
On admet que la variable aléatoire L suit la loi normale d’espérance μ et d’écart type s.
Une vis est considérée comme conforme lorsque sa longueur est comprise entre 59,60 mm et 60,40 mm.
1. Dans cette question, on suppose que µ = 60 et s = 0,25. La probabilité qu’une vis choisie au hasard dans le stock soit conforme est, d’après la calculatrice :
P(59,60 < X < 60,40) ≈ 0,89.
2. Les vis sont considérées conformes si leur longueur moyenne est de 60 mm. Afin de vérifier le bon réglage des machines de fabrication des vis produites par la première chaîne de production, on construit un test d’hypothèse bilatéral relativement à la moyenne des longueurs des vis, au seuil de risque de 5 %. L’hypothèse nulle du test est donc H0 : µ = 60.
a. Le test est bilatéral : l’hypothèse alternative H1 est µ diffère de 60.
On note LY la variable aléatoire qui, à chaque échantillon de 100 vis produites par la première chaîne„ associe la moyenne des longueurs de ces 100 vis. Sous l’hypothèse H0, on admet que LY suit la loi normale d’espérance mathématique 60 et d’écart type s ′ = 0,025.
b. On admet que P ( 59,95 < Y < 60,05)= 0,95.
Règle de décision : si la moyenne des longueurs des 100 vis de l’échantillon n’appartient pas à l’intervalle [ 59,95 : 60,05] , alors on rejette l’hypothèse nulle, au risque de 5 %; sinon, on ne peut pas rejeter l’hypothèse nulle.
c. On prélève un échantillon de 100 vis et on obtient, pour cet échantillon, une moyenne des longueurs des 100 vis égale à 60,03 mm.
60,03 appartient à [59,95 : 60,05] donc on ne peut pas rejeter l’hypothèse H0 au risque de 5 %. Il n’y a donc pas lieu d’effectuer un réglage de la première chaîne de production.