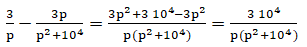Mathématiques,
équation différentielle, lois normale, binomiale, test, transformée de
Laplace,
BTS groupe B 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
. |
..
..
......
...
|
Exercice 1. 10
points.
On coule du béton pour faire une dalle. Au début, le béton est mou,
puis, au fil du temps, il sèche, et devient plus résistant.
On note f (t ) la résistance du béton à l’instant t .
f (t ) est exprimée en mégapascal (MPa) et t désigne le nombre de jours
de séchage.Partie A. Résolution d’une équation différentielle
On admet que la fonction f est solution de l’équation différentielle :
(E) : y′ +0,06y = 2,1,
où y est une fonction inconnue de la variable réelle t , définie et
dérivable sur [0 ; +∞[ et où y′ est la dérivée de y.
1. Résoudre sur [0
; +∞[ l’équation différentielle :
(E0) : y′+0,06y = 0.
y = A e-0,06t avec A une constante.
2. On considère la
fonction constante g définie sur [0 ; +∞[ par g(t )= 35.
Vérifier que la fonction g est solution de l’équation différentielle
(E).
g'(t) =0 ; 0+0,06 *35 =2,1.
3. En déduire
l’ensemble des solutions de l’équation différentielle (E).
y = A e-0,06t +35.
4. À l’instant t = 0, on considère
que la résistance du béton est nulle.
En déduire que la fonction f est définie sur [0 ; +∞[ par : f (t )= −35e−0,06t
+35.
0 = A+35 ; A = -35.
f (t )= −35e−0,06t +35.
Partie B. Étude de fonction
On considère à nouveau la fonction f définie sur [0 ; +∞[ par :
f (t ) =−35e−0,06t +35.
On rappelle que f (t ) désigne la résistance du béton, exprimée en
mégapascal, à l’issue de t jours de séchage.
1. Quelle est la
résistance du béton après 7 jours de séchage ? Après 72 heures ?
Arrondir au dixième.
f(7) = -35 exp(-0,06x7) +35 =12,0 MPa.
f(3) = -35 exp(-0,06x3) +35 =5,8
MPa.
2. On admet
que la fonction f est dérivable sur [0 ; +∞[ et on note f ′ sa fonction
dérivée.
Vérifier que, pour tout réel t appartenant à [0 ; +∞[, on a :
f ′(t ) =2,1e−0,06t .
f '(t) = -35 x(-0,06) exp(-0,06t) = 2,1 exp(-0,06t).
3. Déterminer le
signe de f ′(t ) sur [0 ; +∞[ et en déduire le sens de variations de f .
exp(-0,06t est positif ; f '(t) >0 et f(t) est strictement
croissante.
4. Déterminer la
limite de f (t ) lorsque t tend vers l’infini.
Interpréter le résultat dans le contexte de l’exercice.
Le terme en exponentielle tend vers zéro et f(t) tend vers 35 MPa.
Au bout d'un temps suffisamment long la résistance du béton atteint 35
MPa.
5. Le fabricant du
béton affirme que la résistance après 28 jours de séchage correspond à
80% de la résistance finale.
Cette affirmation est-elle juste ?
f(28)=-35 exp(-0,06 x28) +35 =28,5 MPa.
35 x0,8 =28 MPa. l'affirmation est correcte.
6. On considère la
fonction F définie sur [0 ; +∞[ par
F(t )= (1750 / 3)e−0,06t +35t .
Montrer que la fonction F est une primitive de la fonction f sur
l’intervalle [0 ; +∞[.
F '(t) = 1750 / 3 x(-0,06)e−0,06t
+35 =−35e−0,06t +35 = f(t).
7. Déterminer une
valeur approchée au dixième de la valeur moyenne de la résistance du
béton sur les 28 premiers jours.
µ =( F(28)-F(0) ) / 28 ; F(28) =1750 / 3 exp(-0,06 x28)+35 x28 =871,3.
F(0) =1750 /3 =583,3 ; µ = (871,3-583,3) /28=10,3 MPa.
Partie C. Algorithme
On note N le nombre entier correspondant au nombre minimal de jours de
séchage permettant d’obtenir une résistance au moins égale à 21 MPa.
1. Recopier
l’algorithme ci-dessous et compléter les lignes 3 et 4.
Ligne 1 : t ←0
Ligne 2 : R ←0
Ligne 3 : Tant que R < =21
Ligne 4 : t ←t+1
Ligne 5 : R ← -35e−0,06t +35
Ligne 6 : Fin Tant que
2. Donner la valeur
de N. Expliquer la démarche suivie.
-35e−0,06t +35 > 21 ;
(35-21) /35 > e−0,06t ; 0,4 > e−0,06t ;
ln(0,4) > -0,06 t
; t > -ln(0,4) /
0,06 ; t >15,3
; N = 16.
|
...
|
....
|
Exercice 2 10 points
Partie A. Loi normale.
Une entreprise produit des tiges métalliques cylindriques.
On note X la variable aléatoire qui, à toute tige prélevée au hasard,
associe son diamètre exprimé en millimètres.
On admet que X suit la loi normale de moyenne μ = 32 et d’écart-type s= 0,6.
1. Donner la
probabilité, arrondie au millième, que le diamètre de la tige prélevée
ait un diamètre compris entre 31 et 33 mm.
P(X < 33)=0,9522.
P(X < 31)=0,0478.
P(31 < X < 33) = 0,904.
2. Déterminer,
aumillième près, le réel h tel que :
P(X > 32−h) = 0,975.
P(X >32-h)=1-P(X <32-h)
=0,975 ; P(X <32-h)=0,025.
32-h =30,824 ; h = 1,176 mm.
Partie B. Loi binomiale.
Une entreprise dispose de 15 imprimantes fonctionnant indépendamment
les unes des autres.
On se place un jour donné.
On considère une imprimante quelconque. La probabilité qu’elle tombe en
panne ce jour est égale à 0,07.
On considère la variable aléatoire Y qui compte le nombre d’imprimantes
qui tombent en panne ce jour.
1. Donner la loi
suivie par Y , ainsi que ses paramètres et son espérance.
Les pannes sont indépendantes. Y suit une loi
binomiale de paramètres n
= 15 et p = 0,07.
Espérance E = np = 15 x0,07= 1,05.
2. Calculer la
probabilité qu’exactement 12 imprimantes ne tombent pas en panne ce
jour.
Probabilité qu'exactement 3 imprimantes tombent en panne = (15 3) x0,073 x(1-0,07)15-3 ~0,065.
3. Calculer la
probabilité qu’au moins 3 imprimantes tombent en panne ce jour.
P(Y >3) = 1 -P(Y< 2)=0,083.
Partie C. Test d’hypothèse
Une entreprise commercialise des blocs de béton de chanvre. Elle
affirme que la résistance moyenne μ de ces blocs est égale à 50
mégapascals (MPa).Désirant vérifier la validité de cette affirmation,
un contrôleur met en place un test d’hypothèse bilatéral.
On note Z la variable aléatoire qui, à chaque bloc prélevé au hasard
dans la production, associe sa résistance, exprimée enMPa.
La variable aléatoire Z suit une loi normale de moyenne inconnue μ et
d’écart-type s=
0,35.
Soit n un entier naturel. On désigne par X la variable aléatoire qui, à
chaque échantillon aléatoire de n blocs prélevés dans la production,
associe la moyenne des résistances de ces blocs.
On rappelle que la variable aléatoire X suit la loi normale de moyenne
μ et d’écart-type s/n½.
L’hypothèse nulle H0 est : « μ = 50 ».
L’hypothèse alternative H1 est : « μ diffère de 50 ».
Le seuil de signification du test est fixé à 5%.
On se place dans le cas où n = 80.
1. Sous l’hypothèse
nulle H0, justifier que la variable aléatoire X suit la loi normale de
moyenne 50 et d’écart-type 0,04.
La variable aléatoire X suit la loi normale de moyenne μ =50 et
d’écart-type s/n½=0,35
/80½ ~0,04.
2. On souhaite
déterminer sous l’hypothèse H0, le réel positif h tel que :
P(50−h < X <
50+h) =0,95.
La valeur du nombre réel h est :
0,05; 0,04 ; 0,08 ; 0,12.
Au seuil de risque de 5 %, h =1,96 x 0,04~0,08.
3. Énoncer la règle
de décision permettant d’utiliser ce test.
[
50-0,08 ; 50 +0,08 ] soit [ 49,92 ; 50,08 ].
Si
la résistance du bloc appartient à cet intervalle, H0 est
vraie, sinon on retient H1.
4. Le contrôleur a
prélevé un échantillon de 80 blocs.
Les résistances obtenues ont été notées dans le tableau ci-dessous.
Résistance
(MPa)
|
49,7
|
49,8
|
49,9
|
50
|
50,2
|
50,4
|
50,5
|
Total
|
Effectif
|
2
|
5
|
15
|
24
|
17
|
13
|
4
|
80
|
Résistance
x effectif
|
99,4
|
249
|
748,5
|
1200
|
853,4
|
655,2
|
202
|
4007,5
|
Appliquer le test et conclure.
4007,5 /80=50,09.
Cette valeur n'appartient pas à
[ 49,92 ; 50,08 ]. On retient l'hypothèse H1.
On considère un
circuit LC.
Le signal d’entrée est noté e(t ). Le signal de sortie est noté s(t ).
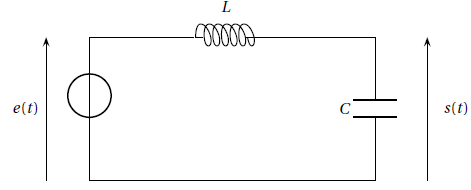
Le système est régi par l’équation différentielle
(E) : LCs′′(t )+s(t )= e(t ).
Les conditions initiales sont : s (0+)=0 et s′ (0+)=
0.
1. On sait que L
=10 H et C = 10−5 F.
Réécrire alors l’équation différentielle (E).
10-4 s"(t)+s(t) =e(t).
2. On suppose que :
La fonction e(t ) admet une transformée de Laplace notée E(p)
La fonction s(t ) admet une transformée de Laplace notée S(p).
Démontrer que l’on a :(10−4p2 +1)S(p)= E(p).
Fonction s"(t) : transformée de Laplace : p2S(p)
Fonction s(t) : transformée de Laplace : S(p).
Fonction e(t) : transformée de Laplace : E(p).
(10−4p2 +1)S(p)= E(p).
3. La fonction de transfert H(P) est
définie par : S(p)= H(p)×E(p).
Démontrer que l’on a :H(p)=104/(p2 +104)
.
H(p) = S(p) / E(p) = 1 / (10−4p2
+1)=104/(p2 +104)
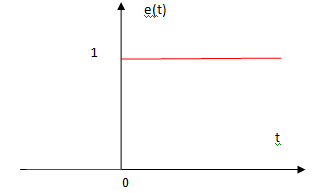
4. On note U(t ) la fonction échelon
unité définie ainsi : U(t )= 0 si t < 0 ; U(t )= 1 si t >0
On suppose désormais que l’on a : e(t )=U(t ).
Représenter graphiquement sur votre copie le signal e(t ) en prenant
pour échelle 1 cm pour chaque axe.
5. Donner
l’expression de E(p).
E(p) = 1 / p.
6. À l’aide des
questions précédentes, déterminer S(p) puis démontrer que l’on a : S(p)
=3 / p-3p /(p2 +104).
S(p)= 104/(p2 +104) E(p)
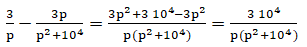
7. En déduire
l’expression de s(t ).
Transformée de Laplace : p / (p2 +104) ; fonction : cos(100 t).
Transformée de Laplace : 1/p ; fonction : U(t).
s(t) = 3 U(t) [1- cos(100t)].
8. On admet que
l’on a :
s(t )= 3U(t )[1−cos(100t )].
Indiquer, sans justifier, lequel des croquis ci-dessous représente la
courbe de la fonction s(t ).
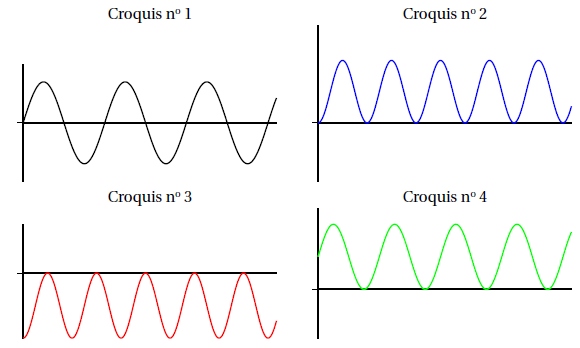
U(t) > 0.
Si t = 0 ; cos(100t) = 1 ; 1-cos(100t) = 0; s(0) = 0. Croquis 3 et 4
éliminés.
-1 < -cos(100t) < 1 ; 0 < 1-cos(100t) < 2 ; s(t) est positif :
croquis 1 éliminé.
|
ane.
|
|
|