Solution
de soude . Bts CIRA 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Dilution de la solution de soude caustique et refroidissement :
Titre massique de la soude : 50 % ; volume de la cuve : 56 m3. Produit corrosif, provoque de grave brûlures.
1. Quel pictogramme de sécurité trouve t-on sur la fiche de sécurité de la soude ?

A l'arrivée du camion un prélevement est effectué. Le densimètre permet de vérifier le titre massique de la soude..
2. A l'aide de la courbe suivante, déterminer la valeur que doit indiquer le densimètre..
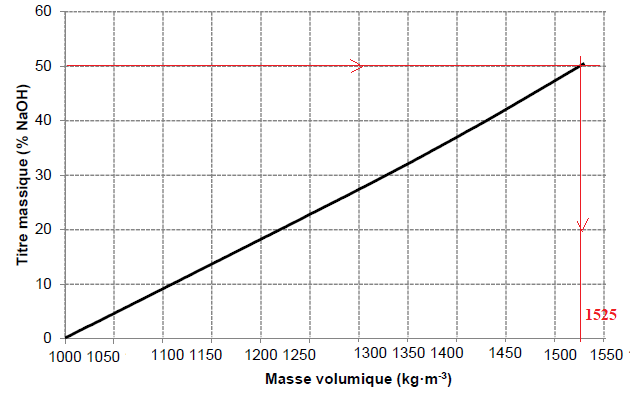
3. La soude à 50 % est diluée avec de l'eau adoucie. Justifier que la dilution est exothermique.
Température de la soude 50 % avant dilution : 40°C.
Température de l'eau servant à la dilution : 22°C.
Température du mélange après dilution : 60°C.
La température finale du mélange après dilution est supérieure aux températures initiales de l'eau et de la soude 50 %.
4. La solution S1 ( soude à 30%) est refroidie de q1= 60°C à q2=40°C. Le fluide servant de refroidssement est de l'eau dont la température d’entrée vaut q3=14 °C, la température de sortie valant q4=42 °C.
Déterminer la valeur de la surface S de l’échangeur à plaques. On
considère que l’échangeur est parfaitement isolé et que son coefficient
global d’échange est K = 303 W.m–2·K–1.
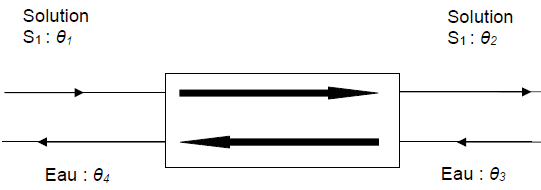 Puissance cédée par la soude S1 ( débit massique 3000 kg / h)
Puissance cédée par la soude S1 ( débit massique 3000 kg / h)
débit massique x capacité thermique massique (3,608 103J kg -1 K-1) x(q2-q1).
3000 x3,608 103 x 20=2,16 108 J / h.
Puissance gagnée par l'eau : débit massique(1850 kg / h) x capacité thermique massique (4,18 103J kg -1 K-1) x(q4-q3).
1850 x 4180 x(42-14)= 2,16 108 J / h ou 2,16 108 / 3600 =6,0 104 watts.
Expression de la différence de température moyenne
logarithmique :
DqmL
=( Dqe- Dqs) / ln ( Dqe/Dqs).
Dqe différence de température d'entrée et Dqs différence de température de sortie en choisissant
arbitrairement l'entrée et la sorite de l'échangeur à contre courant.
Dqe = 60-14 = 46°C ; Dqs = 42-40 = 2°C ;
DqmL =(46-2) / ln
(46 /2 ) =14°C.
En
déduire la surface S de l'échangeur. K = 303 W m-2K-1.
Pc = KS DqmL ; S = Pc
/( K DqmL )= 6,0 104 /
(303 * 14) ~14 m2.
Mesure de la température en sortie d’échangeur.
La mesure de température en sortie de l’échangeur thermique s’effectue à l’aide d’une sonde de type Pt100 reliée à un
conditionneur de signal. Le schéma du montage est représenté.
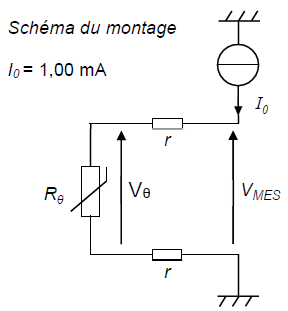
Le conditionneur est relié à la sonde par des fils de cuivre d’une longueur L = 17 m et d’une section S = 0,75 mm2. Conductivité : r = 1,7 10-8 W m.
On se place dans l’étude qui suit à la température de consigne, soit 40 °C.
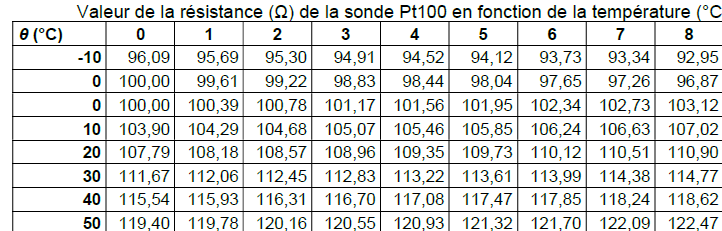
Q5- Déterminer la valeur de V MES dans le cas de fils courts dont la résistance r peut être négligée.
R q = 115,54 W.
VMES =Rq I0 =115,54 x 10-3 =0,115 V.
Q6- Montrer que la valeur de la résistance d’un fil est égale à r = 0,39 W.
r = r L / S =1,7 10 -8 x17 / (0,75 10 -6)= 0,39 W.
Q7- Déterminer la valeur de la résistance équivalente R eq
en tenant compte de la résistance des fils. En déduire, dans cette
configuration, l’erreur introduite sur la mesure de la température.
Req = Rq + 2r =115,54+2 x 0,39=116,32 ohms.
Température indiquée par la sonde 42°C.
Afin
de compenser la longueur des fils, on remplace la sonde « 2 fils » par
une sonde « 3 fils » suivant le montage ci-dessous. La longueur et le
matériau des fils restent identiques au montage « 2 fils ».
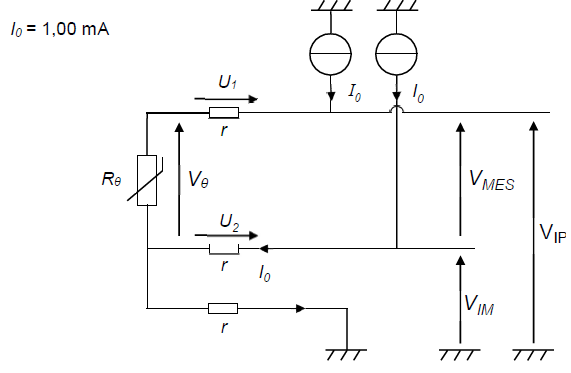
Q8- Déterminer la relation entre VMES, Vq, U1 et U2 puis en déduire que VMES = Rq×I0. Conclure quant à l’intérêt de ce montage par rapport au premier.
VMES = Vq + U1 -U2= Rq×I0+ r I0 -r I0 =Rq×I0.
VMES est indépendant de la longueur des fils.
Vérification du titre massique.
L’entreprise
dispose d’un laboratoire d’analyse et un technicien souhaite vérifier
le titre massique de la soude ainsi refroidie.
On introduit un volume V1 = 5,00 mL de la solution S1 dans une fiole jaugée de volume V = 100 mL. On complète avec de l’eau jusqu’au trait de jauge. On obtient la solution S2.
On prélève alors un volume V2 = 10,0 mL de la solution S2 que l’on introduit dans un bécher.
On réalise un dosage colorimétrique par une solution d’acide chlorhydrique S3.
Q10- Une solution aqueuse de soude (hydroxyde de sodium) a pour formule chimique (Na+(aq), HO–(aq)) ; celle d’une solution aqueuse d’acide chlorhydrique est (H3O+(aq), Cl–(aq)).
La transformation chimique entre les ions hydroxyde et les ions oxonium
peut être modélisée par la réaction dont l’équation chimique est :
H3O+(aq) +HO–(aq)--> 2 H2O(l).
Indiquer, en justifiant, la nature de la réaction mise en jeu.
Réaction acide base : échange de proton entre l'acide H3O+(aq) et la base HO–(aq).
Q11- Le volume d’acide chlorhydrique permettant d’obtenir l’équivalence a pour valeur V3éq = 12,0 mL.
La concentration molaire de l’acide chlorhydrique a pour valeur c3 = 0,415 mol·L–1.
Déterminer les valeurs des concentrations molaires des solutions S2 et S1 notées respectivement c2 et c1.
A l'équivalence du titrage : c3V3éq =V2c2 ; c2 = c3V3éq / V2 = 0,415 x12,0 / 10,0 =0,498 mol / L.
c1 = 100 / 5 c2 =20 x0,498 = 9,96 mol / L.
Q12- La masse volumique de la solution S1 a pour valeur 1,33×103 g·L–1. La masse molaire de l’hydroxyde de sodium étant de 40,0 g·mol–1, calculer la valeur du titre massique de la solution S1 et indiquer si la solution est conforme.
9,96 x40,0 =398,4 g / L ; masse de 1 L de solution : 1,33×103 g.
Titre massique : 398,4 / (1,33 103) x100 ~ 30 %, valeur différente de 50 %, solution non conforme..
|
...
|
....
|
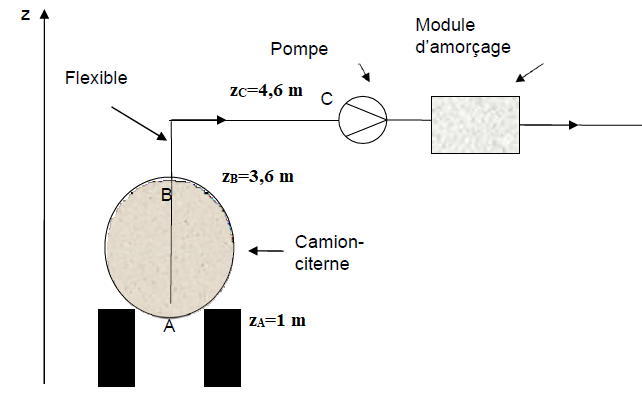
Q13- Calculer la valeur de la pression au point A avant que la pompe soit active et vérifier qu’elle est proche de 1,40×105 Pa.
PA = rsoude g (zB-zA) + Patm= 1504 x9,81 x 2,6+1,02 105=1,40×105 Pa.
Q14- La cuve d’une contenance de 53 m3 est vidée en 2 heures. Calculer la valeur de la vitesse d’écoulement de la soude dans le flexible de diamètre D = 65 mm.
Débit : 53 / (2 x3600)=7,36 10-3 m3 /s.
Section : 3,14 x0,0652 /4 =3,32 10-3 m2.
Vitesse d'écoulement = débit / section=7,36 / 3,32 ~2,22 m /s.
Q15- Déterminer la valeur du nombre de Reynolds Re et qualifier la nature du régime d’écoulement.
Re = rsoude v D / h =1504 x 2,22 x 0,065 / 0,079~2,74 103 compris entre 2000 et 3000, régime intermédiaire.
Q16- En utilisant le théorème de Bernoulli entre les points A et C, vérifier que la pression PC vaut 6,8×104 Pa. Les pertes de charges singulières seront négligées.
Pertes de charges J = l (L / D) v2 /(2g).
l = (100 Re)-0,25 =(2,74 105)-0,25=0,044.
J = 0,044 x( 6 /0,065) x2,222 /(2*9,8)=1,0 joule.
½v2A + gzA + PA / rsoude = ½v2C + gzC + PC / rsoude .
vA << vC ; PC = rsoude g(zA-zC)+ PA - ½v2C rsoude =1504 x9,81 x(-3,6) +1,4 105 -0,5 x2,222 x1504 ~8,3 104 Pa.
Q17- Calculer le NPSH disponible et déterminer s’il y a un risque de cavitation.
NPSH dispo =[PC /(rsoude g)+v2C /(2g)]-PVS / (rsoude g).
NPSH dispo =[6.8 104 /(1504x9,8)+2,222 /(2x9,8)]-200/ (1504x9,8)=4,16.
Le NPSH requis est d'environ 2,1 m pour ce débit ( 26,5 m3 / h).
NPSH dispo -NPSH >0 : donc pas de cavitation.
|
|