La
maladie de Lyme, bts Analyses de Biologie Médicale 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1 : diagnostiquer la maladie. 9 points.
A. Diagnostic direct par microscopie.
Distance focale de l'objectif f '1 = 4 mm ; distance focale de l'oculaire : f '2 =25 cm.
Une bactérie Borrelia est modélisée par une flèche AB, placée perpendiculairement à l'axe optique.
L'oeil n'accommode pas : l'image intermédiaire A1B1 donnée par l'objectif se forme dans le plan focal objet de l'oculaire.
Q1. Indiquer où se situe l'image définitive A'B'.
L'image définitive se trouve à l'infini.
Q2. Compléter le schéma du dispositif.
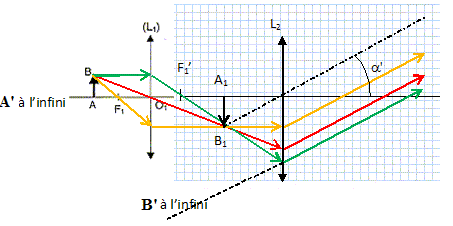 L'objet est placé à 4,1 mm de l'objectif.
L'objet est placé à 4,1 mm de l'objectif.
Q3. Calculer F'1F'2.
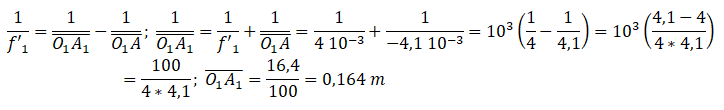
F'1F'2.=O1A1 -O1F'1 = 0,164 -0,004 = 0,16 m.
Q4. Expliquer ce qu'est le pouvoir de résolution du microscope.
C'est la distance minimale entre deux points contigus pour qu'ils soient correctement discernés par le microscope.
La longueur d'onde de la lumière utilisée est de 600 nm. Les borrelia
sont des bactéries de diamètre 0,40 µm. On souhaite les observer à
travers le microscope.
Q5.
Le miroscope dispose de 4 objectifs d'ouverture numérique 0,16 ; 0,40 ;
0,70 et 0,95. Choisir celui ou ceux qui permettront cette observation.
Justifier.
Pouvoir séparateur du microscope : e = 0,6 l / ouverture numérique.
e =0,6 x600 / 0,16 =2250 nm = 2,25 µm, valeur supérieur à la dimension de borrelia.
e =0,6 x600 / 0,40 =900 nm = 0,9 µm, valeur supérieur à la dimension de borrelia.
e =0,6 x600 / 0,70 =514 nm = 0,51 µm, valeur supérieur à la dimension de borrelia.
e =0,6 x600 / 0,95 =379 nm = 0,38 µm, valeur inférieur à la dimension de borrelia.
L'ouverture numérique 0,95 convient à l'observation de la bactérie.
B. Diagnostic indirect par la méthode ELISA.
Le protocole conduit à la coloration finale jaune-orangé du milieu, due à la réaction entre le peroxyde d'hydrogène et le TBM.
La coloration dépend de la quantité d'enzymz liée aux anticorps. Le dosage peut être réalisé à partir d'une courbe d'étalonnage.
Q6. Définir le terme catalyseur.
Un catalyseur accélère une réaction chimique thermodynamiquement possible et n'apparaît pas dans le bilan.
Q7. Ecrire les demi-équations des couples TBMox / TBMH2red et H2O2/H2O.
TBMH2red =TBMox +2H++2e- .
H2O2+2H++2e- =2H2O.
Q8. En déduire l'équation de la réaction entre TBMH2red et H2O2.
TBMH2red +H2O2-->TBMox +2H2O.
Q9. On choisit l = 450 nm comme longueur d'onde de travail pour réaliser les mesures spectrophotométriques. Montrer que ce choix est cohérent.
La couleur complémentaire du jaune orangé est le bleu violet ( 450 nm).
Pour une meilleure précision, on se place à la longueur d'onde du
maximum d'absorption.
Les mesures conduisent à la courbe suivante :
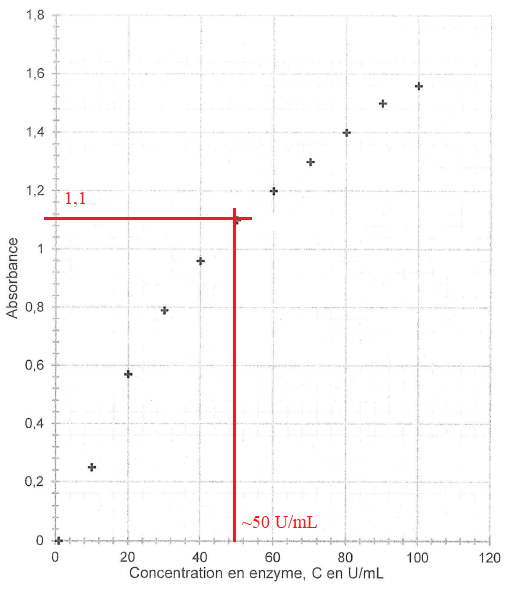
Q10. L'échantillon de plasma d'un patient donne A = 1,1. La suspicion de la maladie de Lyme est-elle fondée ?
C = 50 U/mL, valeur supérieure à 11 U/mL ; le test étant positif, la suspicion de la maladie de Lyme est fondée.
|
...
|
....
|
Exercie 2. Soulager la maladie (11 points).
A. Les antibiotiques.
Q11. Entourer et nommer les groupes fonctionnels de l'amoxicilline qui permettent de distinguer les deux molécules.
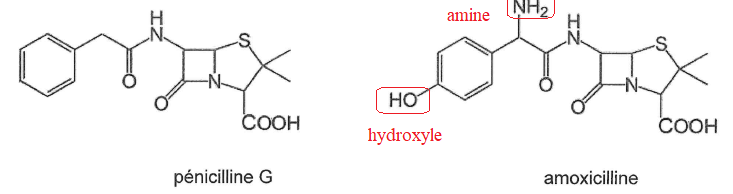
Q12. Justifier que l'amoxicilline est plus hydrophile que la péniciline G.
L'amoxicilline possède un groupe hydroxyle et un groupe amine de plus
par rapport à la péniciline G. Ces deux groupes sont hydrophiles.
Q13. Justifier que le carbone 2 est de configuration absolue S.
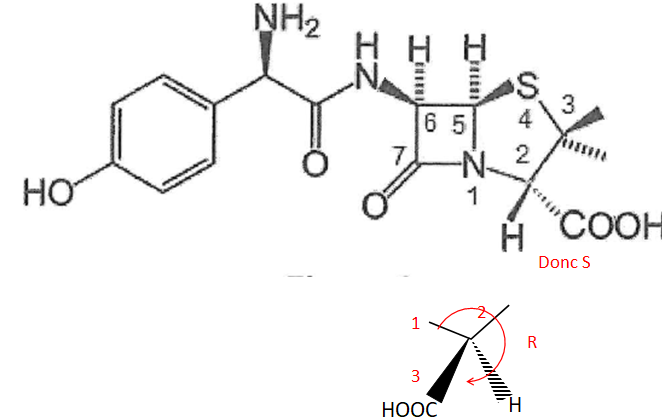
Q14. Justifier que
l'amoxicilline possède un atome de carbone asymétrique
supplémentaire par rapport à la péniciline G. Le repérer.
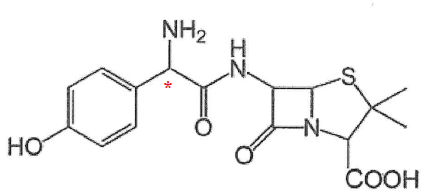
Q15.
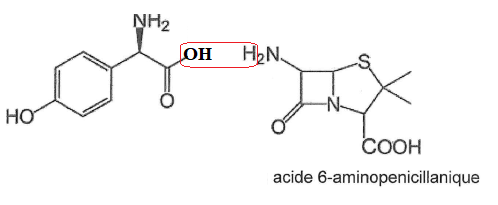
Proposer en la dessinant et en justifiant le choix opéré, la formule
semi-développée d'une molécule qui pourrait réagir, en une seule étape,
avec l'acide 6-aminopenicillanique pour former la molécule
d'amoxicilline.
Le chlorure de magnésium.
On fabrique la solution S0 en dissolvant m = 0,20 g de poudre de sel de Nigari ( contient plus de 90 % de chlorure de magnésium hexahydraté) dans V0 = 100,00 mL d'eau distillée. La solution est diluée 10 fois ( solution S1).
On titre V1 = 100,0 mL de S1 par une solution d'hydroxyde de sodium de concentration C = 0,010 mol / L.
Q16. Ecrire l'équation de la réaction de dissolution de chlorure de magnésium hexahydraté.
MgCl2, 6H2O(s) --> Mg2+aq +2Cl-aq + 6H2O(l).
On donne l'équation de la réaction support du titrage.
Mg2+aq +2HO-aq --> Mg(OH)2 (s).
Q17.1. Exprimer la
constante d'équilibre Kr de cette transformation en fonction du produit
de solubilité Ks de l'hydroxyde de magnésium.
Ks = [Mg2+][HO-]2.
Kr = 1 /([Mg2+][HO-]2) = 1 / Ks = 1 / (5,6 10-12) =1,8 1011.
Q17.2. Justifier le caractère total de cette transformation.
Kr est très grand, la transformation est donc totale.
Q17.3. Indiquer quelle autre condition cinétique doit respecter la réaction support du titrage.
Elle doit être rapide.
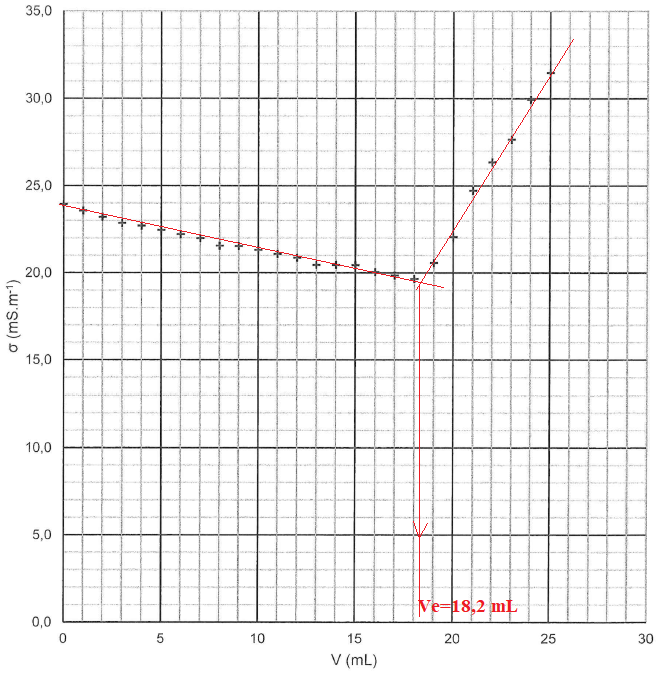
Q18. Justifier l'allure du graphique.
Avanrt l'équivalence, l'ion hydroxyde est en défaut. Du point de vue de
la conductivité, tout se passe comme si on remplaçait l'ion magnésium
par l'ion sodium de conductivité molaire ionique moindre. La
conductivité de la solution diminue.
Après l'équivalence, l'ion hydroxyde est en excès et on ajoute des ion sodium : la conductivité de la solution croît rapidement.
Q19. Calculer la concentration en ion magnésium.
A l'équivalence : n(HO-) = C Ve = 0,010 x 18,2 = 0,182 mmol.
n(Mg2+) = ½n(HO-) = 0,091 mmol dans 100 mL de S1.C1 = 0,091 /100 = 9,1 10-4 mol / L.
Tenir compte de la dilution : C0 = 9,1 10-3 mol / L.
Soit 9,1 10-4 mol dans 100 mL ou dans 0,20 g de poudre.
M(MgCl2, 6H2O) = 206,3 g/ mol.
Masse de chlorure de magnésium hexahydraté : 9,1 10-4 x 206,3 ~0,19 g.
Pourcentage massique 0,19 / 0,20 x100 =95 %.
Cette valeur est en accord avec l'indication de l'étiquette.
|
ane.
|
|
|